【LeetCode】4. 寻找两个正序数组的中位数

题目链接

二分查找

常见复杂度排序： $O(1)<O(\log n)<O(n)<O(n\log n)<O(n^2)<O(n^3)<O(2^2)<O(n!)<O(n^n)$

中位数 定义： 将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。
k = (len(nums1)+len(nums2)+1)//2
奇数： 实际中位数为 k-1
偶数： 实际中位数为 k, k-1 两者的均值

Python3

方法一： 二分查找 $⟮O(\log (m+n))、O(1)⟯$

页面内跳转： 查看补充内容增强理解

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        # 子模块： 查找  第 k 小 的数  
        def getKthElement(k):
            index1, index2 = 0, 0  # 剩余元素 的起始下标
            while True:
                # 递归 跳出 条件
                if index1 == m:  # nums1 的元素 已被全部去掉   注意 nums1最后一个元素的下标是 m-1
                    return nums2[index2 + k - 1] # 直接在 nums2剩余元素中 返回 第 k 小 的数
                if index2 == n:  # 
                    return nums1[index1 + k - 1]
                if k == 1:  ## 在剩下的元素里 返回 第 1 小的元素
                    return min(nums1[index1], nums2[index2])
                
                # 一般情况
                newIndex1 = min(index1 + k // 2 - 1, m-1) # 要是 newIndex1 == m, 就要跳出了
                newIndex2 = min(index2 + k // 2 - 1, n-1)
                pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
                if pivot1 <= pivot2:
                    k -= newIndex1 - index1 + 1 # 更新 k 
                    index1 = newIndex1 + 1 
                else:
                    k -= newIndex2 - index2 + 1
                    index2 = newIndex2 + 1
                
        m, n = len(nums1), len(nums2)
        totalLength = m + n 
        if totalLength % 2 == 1: # 奇数
            return getKthElement((totalLength + 1) // 2)
        else:  # 偶数
            return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) /2            
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

⭐ 方法二： 划分数组 $⟮O(\log (\min (m,n))、O(1)⟯$

中位数的作用： 将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if len(nums1) > len(nums2): # 保证  nums1 是较短的
            return self.findMedianSortedArrays(nums2,nums1) 
        
        m, n = len(nums1), len(nums2) 
        left, right = 0, m  # 两个 数组 在 合并数组的 填充起始下标
        median1 = 0  # 前一部分的 最大值 
        median2 = 0  # 后一部分的 最小值

                
        while left <= right:
            i = (left + right) // 2
            j = (m + n + 1) // 2 - i  
            # 前一部分包含 nums1的前面部分 和  nums2 的前面部分
            # 后一部分  包含  nums1 的后面部分 +  nums2 的后面部分
 
            # 维护 分界线 附近 的四个数 
            nums_im1 = (-math.inf if i == 0 else nums1[i-1]) # i minus 1   nums1 前半部分 最大值
            nums_i = (math.inf if i == m else nums1[i])    # nums1 后半部分 最小值
            nums_jm1 = (-math.inf if j == 0 else nums2[j-1])  # nums2 前半部分 最大值
            nums_j = (math.inf if j == n else nums2[j])   # nums2 后半部分 最小值

            if nums_im1 <= nums_j:
                median1, median2 = max(nums_im1, nums_jm1), min(nums_i,nums_j)
                left  = i + 1
            else:
                right =  i - 1

        return (median1 + median2) / 2 if (m + n) % 2 == 0 else median1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

方法： 额外数组归并，直接定位中位数 $⟮O(m+n)⟯$

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        """额外数组"""
        nums = []
        i, j = 0, 0
        while i < len(nums1) and j < len(nums2):
            if nums1[i] <= nums2[j]:
                nums.append(nums1[i])
                i += 1
            else:
                nums.append(nums2[j])
                j += 1

        if i < len(nums1):
            nums.extend(nums1[i:])
        if j < len(nums2):
            nums.extend(nums2[j:])

        n = len(nums)
        if n % 2 == 0: ### 偶数个
            m = n // 2   ## 10//2 = 5  中间下标4， 5 
            return (nums[m-1] + nums[m])/2

        else: 
            return nums[n//2]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

C++

方法一： 二分查找 $⟮O(\log (m+n))、O(1)⟯$

class Solution {
public:
    // 子模块
    int getKthElement(vector<int>& nums1, vector<int>& nums2, int k){
        int index1 = 0, index2 = 0;
        int m = nums1.size(), n = nums2.size();

        while (true){
            // 跳出条件
            if (index1 == m){
                return nums2[index2 + k - 1];
            }
            if (index2 == n){
                return nums1[index1 + k -1];
            }
            if (k == 1){
                return min(nums1[index1], nums2[index2]);
            }

            // 一般情况
            int newIndex1 = min(index1 + k / 2 - 1, m - 1);
            int newIndex2 = min(index2 + k / 2 - 1, n - 1);
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            if (pivot1 < pivot2){
                k -= newIndex1 - index1 + 1;
                index1 = newIndex1 + 1;
            }
            else{
                k -= newIndex2 - index2 + 1;
                index2 = newIndex2 + 1;
            }
        }
    }
    // 主模块
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        int TotalLength = m + n; 
        if (TotalLength % 2 == 1){// 奇数
            return getKthElement(nums1, nums2, (TotalLength + 1)/2); // 注意 写法
        }
        else{ // 偶数
            return (getKthElement(nums1, nums2, TotalLength / 2) + getKthElement(nums1, nums2, TotalLength / 2 + 1))/2.0;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

⭐ 方法二： 划分数组 $⟮O(\log (\min (m,n))、O(1)⟯$

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()){
            return findMedianSortedArrays(nums2, nums1);
        }

        int m = nums1.size(), n = nums2.size();
        int left = 0, right = m;
        int median1 = 0, median2 = 0; // 前一部分的 最大值   后一部分的最小值

        while (left <= right){
            int i = (left + right) / 2; // nums1 分界
            int j = (m + n + 1)/2 - i;  // nums2 分界

            // 维护 分界线 附近的 四个数
            int nums_im1 = (i == 0 ?  INT_MIN : nums1[i-1]);
            int nums_i = (i == m ? INT_MAX : nums1[i]) ;  // nums1 右侧的最小值
            int nums_jm1 = (j == 0 ? INT_MIN : nums2[j-1]);  
            int nums_j =(j == n ? INT_MAX : nums2[j]);

            if (nums_im1 <= nums_j){// 最大值  小于 最小值
                median1 = max(nums_im1, nums_jm1);
                median2 = min(nums_i, nums_j);
                left = i + 1;
            }
            else{
                right = i - 1;
            }
        }
        return (m + n) % 2 == 0 ? (median1 +median2) / 2.0 : median1;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

二分查找 理解

参考链接



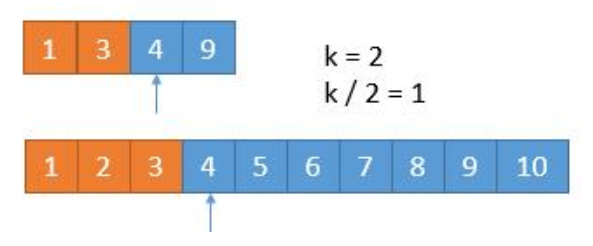
这时 两个位置的数 相等，去掉其中一个即可

比较 得到 第7小 为 4

特殊情况：

返回之前的地方