使用Java实现汉诺塔问题~

分治算法：

见名识义，分而治之，其实就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题.…直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

分治算法思想适用于解决一些具有重叠子问题的问题，例如排序、搜索、遍历等。通过将问题分解为子问题，可以降低问题的复杂度，并且可以利用递归的方式解决子问题。最后，将子问题的解进行合并，得到原问题的解。

汉诺塔：

1. 将大问题分解为三个子问题：将n-1个盘子从起始柱移动到辅助柱，将第n个盘子从起始柱移动到目标柱，将n-1个盘子从辅助柱移动到目标柱。

2. 递归地解决这三个子问题，直到问题规模变为最简单的情况，即只有一个盘子需要移动。

3. 将子问题的解进行合并，即按照分解的步骤将盘子从起始柱移动到目标柱。

我们设A为起始柱子，B为辅助柱子，C为目标柱子

由于盘子只能是大的放在下面，小的放在上面，因此，我们需要先将A柱子除了最下层的盘子都移动至B柱子

如下所示完成了最下层柱子到达它的最终位置，接下来，我们需要将B柱子上除了最下层的盘子之外的盘子移动至A，重复上述步骤

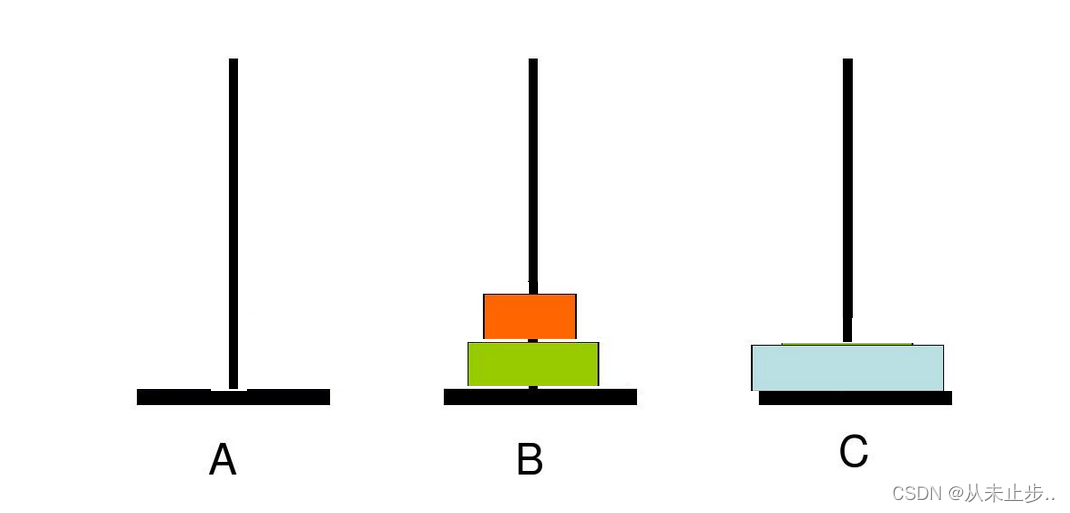
每次变化的点有两个：

1：柱子的功能

默认条件下，我们设置A为初始柱子，B为辅助柱子，C为目标柱子

设圆盘的个数为n

那么第一次我们需要将A柱子上的n-1个盘子借助C按照大小移动至B，由此B成为目标柱子，C为辅助柱子，当最下层的柱子到达C后，第一次完成（A为空柱子，B有n-1个盘子，C有1个盘子）

那么第二次我们需要将B柱子上的n-1-1个盘子借助A按照大小移动至C，由此C成为目标柱子，A为辅助柱子，当最下层的柱子到达C后，第二次完成（A有n-1-1个盘子，B为空柱子，C有2个盘子）

…

我们可以将除了最下层之外的n-1个圆盘看作一个整体，其实也就是2个盘子移动的问题，内部就是一个不断递归的过程

2：圆盘的数量

需要移动的圆盘的数量每次完成之后-1，而到达最终位置的圆盘数量每次完成之后+1

实现：

package lanqiaobei;

public class hanioTower {
   
 
	public static void main(String[] args) {
   
		hanioTower(100,'A','B','C');
	
	}
	public static void hanioTower(int nums,char a,char b,char c) {
   
		if(nums==1) {
   
			System.out.println("第1个盘子从"+a+"--->"+c);
		}else {
   
			//1：先将最上面的盘子从A-->B(借助C盘-递归实现)
			//2:将最下面的盘子从A-->C
			//3：将B塔的所有盘从B--->C(借助A盘-递归实现)
			hanioTower(nums-1,a,c,b);
			System.out.println("第"+nums+"个盘子从"+a+"--->"+c);
			hanioTower(nums-1,b,a,c);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

第1个盘子从A--->B
第2个盘子从A--->C
第1个盘子从B--->C
第3个盘子从A--->B
第1个盘子从C--->A
第2
1
2
3
4
5