代码随想录 Day26贪心算法01-上

目录

前言:贪心无套路

本质:

两个极端

 贪心的小例子

贪心无套路!!!

LeetCode T455 分发饼干

题目思路:

1.优先考虑胃口:大饼干喂饱大胃口

2.优先考虑饼干:小饼干先喂饱小胃口

---

前言:贪心无套路

本质:

局部最优去推导全局最优

两个极端

贪心算法的难度一般要么特别简单,要么特别困难,所以我们只能多见识多做题,记住无需数学证明,因为两道贪心基本上毫无关系,我们只需要去思考局部最优即可

 贪心的小例子

比如有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？

那肯定是每次拿最大的就行,局部最优就是每次拿最大数额的钞票,全局最优就是最后数额的总和是最大的.

贪心无套路!!!

这里贪心没有任何的模板总结,因为解决不同问题的贪心策略是完全不同的,我们不需要严格的数学证明,如果面对一道题你有这么一种贪心的策略,同时你找不到任何明显的反例,那么就可以照着这个思路来思考问题... 

LeetCode T455 分发饼干

题目链接:455. 分发饼干 - 力扣（LeetCode）

题目思路:

这题我们有两种思路可以解决问题

1.优先考虑胃口:大饼干喂饱大胃口

这里的局部最优就是充分利用大饼干来喂饱小孩,全局最优就是喂饱尽可能多的小孩

(尽可能让吃饱的人多)

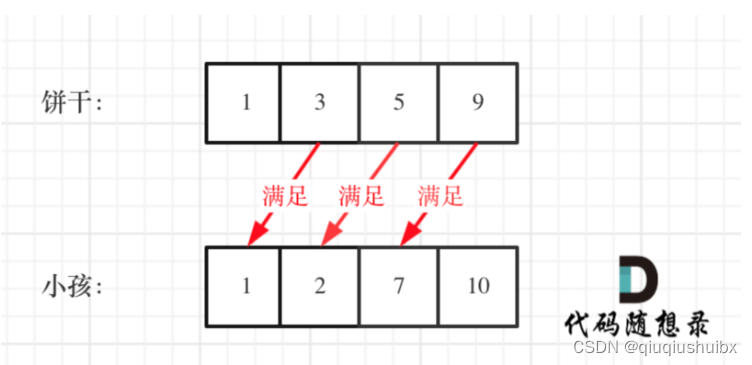
2.优先考虑饼干:小饼干先喂饱小胃口

这里的局部最优是花费掉最小的饼干,让小饼干物尽其用,全局最优是使饼干的花费更有性价比.

(尽可能让饼干发挥最大的效果)

题目代码

//解法一:
class Solution {
    int count = 0;
    int start = 0;
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
 
        for(int i = 0;i
        {
            if(s[i]>=g[start])
            {
                start++;
                count++;
            }
        }
        return count;
 
    }
}
 
//解法2
class Solution {
    int count = 0;
    int start ;
    public int findContentChildren(int[] g, int[] s) {
        start = s.length-1;
        Arrays.sort(g);
        Arrays.sort(s);
 
        for(int i = g.length-1;i>=0;i--)
        {
            if(start >= 0 && s[start]>=g[i])
            {
                start--;
                count++;
            }
        }
        return count;
 
    }
}