-
算法基础学习|前缀和差分
前缀和
代码模板
- 一维前缀和模板
- S[i] = a[1] + a[2] + ... a[i]
- a[l] + ... + a[r] = S[r] - S[l - 1]
- 二维前缀和模板
- S[i, j] = 第i行j列格子左上部分所有元素的和
- 以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
- S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
例题一
题目
输入一个长度为
 的整数序列。
的整数序列。接下来再输入
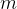 个询问,每个询问输入一对
个询问,每个询问输入一对  。
。
对于每个询问,输出原序列中从第
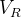 个数到第
个数到第  个数的和。
个数的和。输入格式
第一行包含两个整数
 和
和 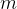 。
。第二行包含
 个整数,表示整数数列。
个整数,表示整数数列。接下来
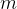 行,每行包含两个整数
行,每行包含两个整数 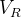 和
和  ,表示一个询问的区间范围。
,表示一个询问的区间范围。输出格式
共
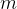 行,每行输出一个询问的结果。
行,每行输出一个询问的结果。数据范围
\(1 \leq l \leq r \leq n\),
\(1 \leq m,n \leq 100000\),
\(-1000 \leq\) 数列中元素的值

输入样例
- 5 3
- 2 1 3 6 4
- 1 2
- 1 3
- 2 4
输出样例
- 3
- 6
- 10
代码示例
- #include
- using namespace std;
- const int N = 100010;
- int a[N],s[N];
- int main(){
- int n, m;
- cin >> n >> m;
- for(int i = 1; i <= n; i++)
- {
- cin >> a[i];
- s[i] = s[i - 1] + a[i];
- }
- int l, r;
- while(m--){
- cin >> l >> r;
- cout << s[r] - s[l - 1] << endl;
- }
- return 0;
- }
例题二
题目
输入一个
 行
行 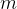 列的整数矩阵,再输入 \(q\) 个询问,每个询问包含四个整数 \(x_1, y_1, x_2, y_2\), 表示一个子矩阵的左上角坐标和右下角坐标。
列的整数矩阵,再输入 \(q\) 个询问,每个询问包含四个整数 \(x_1, y_1, x_2, y_2\), 表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 \(n, m, q\)。
接下来
 行,每行包含
行,每行包含 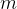 个整数,表示整数矩阵。
个整数,表示整数矩阵。接下来 \(q\) 行,每行包含四个整数 \(x_1, y_1, x_2, y_2\) 表示一组询问。
输出格式
共 \(q\) 行,每行输出一个询问的结果。
数据范围
\(1 \leq n,m \leq 1000\),
\(1 \leq q \leq 200000\),
\(1 \leq x_1 \leq x_2 \leq n\),
\(1 \leq y_1 \leq y_2 \leq m\),
\(-1000 \leq\) 矩阵元素的值

输入样例
- 3 4 3
- 1 7 2 4
- 3 6 2 8
- 2 1 2 3
- 1 1 2 2
- 2 1 3 4
- 1 3 3 4
输出样例
- 17
- 27
- 21
代码示例
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- using namespace std;
- const int N = 1010;
- int m, n, q;
- int s[N][N];
- int main() {
- cin.tie(0);
- ios::sync_with_stdio(false);
- cin >> n >> m >> q;
- for (int i = 1; i <= n; i++)
- {
- for (int j = 1; j <= m; j++) {
- cin >> s[i][j];
- s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
- }
- }
- int x1, y1, x2, y2;
- while (q--) {
- cin >> x1 >> y1 >> x2 >> y2;
- cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;
- }
- }
差分
代码模板
- 一维差分
- 给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
- 二维差分
- 给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
- S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
例题一
题目
输入一个长度为
 的整数序列。
的整数序列。接下来输入
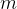 个操作,每个操作包含三个整数 \(l, r, c\),表示将序列中 \([l, r]\) 之间的每个数加上\(c\)。
个操作,每个操作包含三个整数 \(l, r, c\),表示将序列中 \([l, r]\) 之间的每个数加上\(c\)。请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数
 和
和 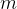 。
。第二行包含
 个整数,表示整数序列。
个整数,表示整数序列。接下来
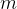 行,每行包含三个整数 \(l,r,c\) 表示一个操作。
行,每行包含三个整数 \(l,r,c\) 表示一个操作。输出格式
共一行,包含
 个整数,表示最终序列。
个整数,表示最终序列。数据范围
\(1 \leq l \leq r \leq n\),
\(1 \leq m,n \leq 100000\),
\(-1000 \leq c \leq 1000\),
\(-1000 \leq\) 数列中元素的值

输入样例
- 6 3
- 1 2 2 1 2 1
- 1 3 1
- 3 5 1
- 1 6 1
输出样例
3 4 5 3 4 2代码示例
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- using namespace std;
- const int N = 100010;
- int a[N], b[N];
- void insert(int l, int r, int c) {
- b[l] += c;
- b[r + 1] -= c;
- }
- int main() {
- int n, m;
- cin >> n >> m;
- for (int i = 1; i <= n; i++)
- {
- cin >> a[i];
- insert(i, i, a[i]);
- }
- while (m--) {
- int l, r, c;
- cin >> l >> r >> c;
- insert(l, r, c);
- }
- for (int i = 1; i <= n; i++) b[i] += b[i - 1];
- for (int i = 1; i <= n; i++) cout << b[i] << " ";
- return 0;
- }
例题二
题目
输入一个
 行
行 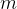 列的整数矩阵,再输入 \(q\) 个操作,每个操作包含五个整数 \(x_1, y_1, x_2, y_2, c\), 其中 \((x_1, y_1)\) 和 \((x_2, y_2)\) 表示一个子矩阵的左上角坐标和右下角坐标。
列的整数矩阵,再输入 \(q\) 个操作,每个操作包含五个整数 \(x_1, y_1, x_2, y_2, c\), 其中 \((x_1, y_1)\) 和 \((x_2, y_2)\) 表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上 \(c\)。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 \(n,m,q\)。
接下来
 行,每行包含
行,每行包含 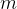 个整数,表示整数矩阵。
个整数,表示整数矩阵。接下来 \(q\) 行,每行包含 5 个整数 \(x_1, y_1, x_2, y_2, c\) 表示一个操作。
输出格式
共
 行,每行
行,每行 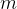 个整数,表示所有操作进行完毕后的最终矩阵。
个整数,表示所有操作进行完毕后的最终矩阵。数据范围
\(1 \leq n,m \leq 1000\),
\(1 \leq q \leq 100000\),
\(1 \leq x_1 \leq x_2 \leq n\),
\(1 \leq y_1 \leq y_2 \leq m\),
\(-1000 \leq c \leq 1000\),
\(-1000 \leq\) 矩阵元素的值

输入样例
- 3 4 3
- 1 2 2 1
- 3 2 2 1
- 1 1 1 1
- 1 1 2 2 1
- 1 3 2 3 2
- 3 1 3 4 1
输出样例
- 2 3 4 1
- 4 3 4 1
- 2 2 2 2
代码示例
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- #include
- using namespace std;
- const int N = 1010;
- int a[N][N], b[N][N];
- void insert(int x1, int y1, int x2, int y2, int c) {
- b[x1][y1] += c;
- b[x2 + 1][y1] -= c;
- b[x1][y2 + 1] -= c;
- b[x2 + 1][y2 + 1] += c;
- }
- int main() {
- cin.tie(0);
- ios::sync_with_stdio(false);
- int n, m, q;
- cin >> n >> m >> q;
- for (int i = 1; i <= n; i++) {
- for (int j = 1; j <= m; j++) {
- cin >> a[i][j];
- insert(i, j, i, j, a[i][j]);
- }
- }
- while (q--) {
- int x1, y1, x2, y2, c;
- cin >> x1 >> y1 >> x2 >> y2 >> c;
- insert(x1, y1, x2, y2, c);
- }
- for (int i = 1; i <= n; i++) {
- for (int j = 1; j <= m; j++) {
- b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
- cout << b[i][j] << " ";
- }
- cout << endl;
- }
- return 0;
- }
-
相关阅读:
【C++之数组与指针2】利用指针对数组求和
vue日历选择
【TES600】青翼科技基于XC7K325T与TMS320C6678的通用信号处理平台
Docker Compose部署Mysql8
【Spring Cloud】教你十分钟学会Gateway~
CentOS 7基础操作10_Linux备份与恢复文档
[BJDCTF2020]EzPHP
C/C++代码中创建销毁进程——内附可执行源码
JS贪吃蛇源码附注释
C语言常考面试基础问题
- 原文地址:https://blog.csdn.net/2203_75720729/article/details/133983978
