计算机算法分析与设计（16）---Dijkstra算法(含C++代码)

---

一、知识概述

1.1 算法描述

1.2 例题分析

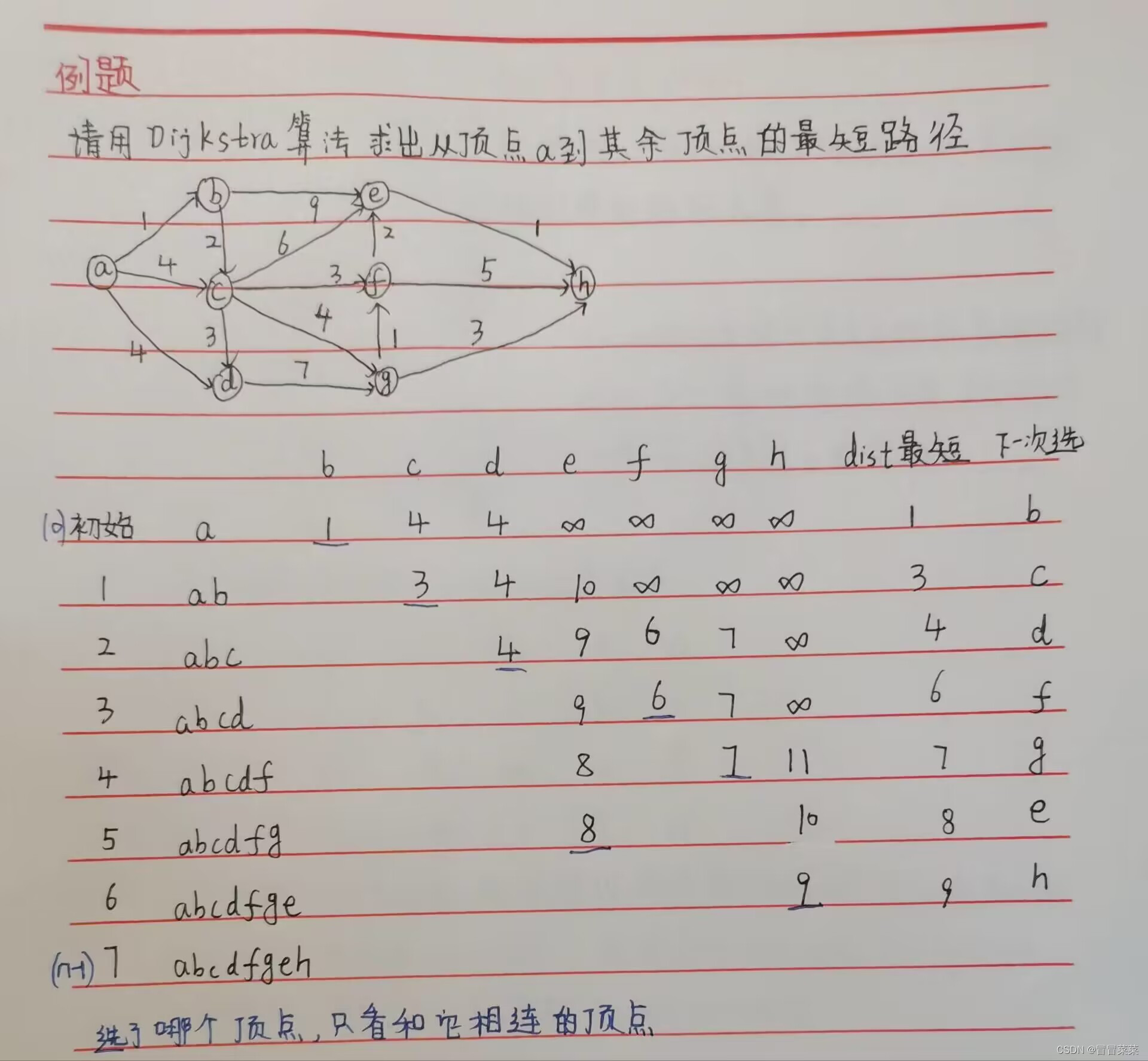
二、代码编写

输入：
 第一行：图的顶点数n
 第二行：图的边数k
 第三行：算法起点begin，算法终点end
 接下来为k行：
 图的点a下标，图的点b下标，a到b的步长len
输出：
 最短距离
样例：
 5
 6
 0 1
 0 2 60
 0 3 30
 0 4 50
 1 2 20
 1 4 10
 3 4 10

#include 
#include 
using namespace std;

#define INF 9999999  //定义不可达，即无穷大 
#define MAXN 200     // 最大顶点数

//low最短距离，visit访问标记
int begin_idx, end_idx, n, k, map[MAXN][MAXN], low[MAXN], visit[MAXN]; 

void dijkstra()
{
    int m_len, index;
    for (int i = 0; i < n; i++)
    {
        low[i] = map[begin_idx][i]; //初始化low，表示从源点到其他点的最短距离 
    }
    for (int i = 0; i < n; i++)
    {
        m_len = INF;
        index = i;
        for (int j = 0; j < n; j++)
        {   //查找最短未访问距离
            if (low[j] < m_len && !visit[j])
            {
                m_len = low[j];
                index = j;
            }
        }
        visit[index] = true;
        
        for (int j = 0; j < n; j++)
        {
            int step_len = m_len + map[index][j];
            if (step_len < low[j])
            {   //是否更新距离
                low[j] = step_len;
                visit[j] = false;
            }
        }
    }
    cout << "最短距离是：" << endl;
    cout << low[end_idx] << endl;
}

int main()
{
    int a, b, len;
    
    cout<<"请输入顶点数："<< endl; 
	cin >> n;            // 顶点数
	
    cout<<"请输入边数："<< endl;
	cin >> k;            // 边数
	
	cout<<"请输入要查询的开始和结束下标："<< endl;
    cin >> begin_idx >> end_idx; // 始末下标
    
	fill(low, low + MAXN, false);     //fill是填充数组值为false 
    fill(visit, visit + MAXN, false); //fill是填充数组值为false
    
    for (int i = 0; i < MAXN; i++)
    {
        fill(map[i], map[i] + MAXN, INF); //先填充两顶点间距离为无穷大 
    }
    
	visit[begin_idx] = true;         //开始结点被访问 
    
    cout << "请输入两顶点及两顶点间的距离：" << endl; 
	for (int i = 0; i < k; i++)
    {
        cin >> a >> b >> len; //输入边的值 
        map[a][b] = map[b][a] = len;
    }
    
    dijkstra();
    return 0;
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78