10.Linear Map transformation rules

线性映射 从一个基底到另一个基底 所遵循的转换规则。

假设：

由一个矩阵给出的线性映射在这，并且是在基底e上表示，

该线性映射将e1变成0.5个e1，将e2变成2个e2；

假设有个向量V，其分量是【1，1】，

L将V转换成L(V),

L(V)的分量是什么？-------------------------------只需将V的列向量与L表示的矩阵相乘。

即* = 

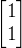所以L(V)的分量是  ， 

所有的这些都是在基底e上完成的，

L(V)= 0.5e1 + 2e2

如果把这些在旧基上表示的分量 应用反向变换，可以得到其在新基中的分量，并注意，使用的是反向转换(Backward)，因为向量分量是逆变的(contravariant)

在此，可能会问，新基中输出的向量的分量是多少？

 新基中输出的向量的分量是多少？--------这个无法用L所表示的矩阵，因为它只适用于旧基（为什么是这样我也不理解），故需要找到一个新矩阵，这个新矩阵告诉我们如何使用新基来构建输出。所以需要计算系数。

计算如下：

也就是说 要将矩阵坐标从旧基转换到新基，我们要将旧矩阵的左侧乘以后向转换(B)，并在旧矩阵的右侧乘以前向转换，。

所以，矩阵或线性映射

实践

检查是否有效

简化上面的推导计算：（技巧1）

观察一下， 发现这些求和的字母符号，有一定规律，其实是可以假装那个求和符号是透明的。

单位矩阵：identity matrix 

技巧2：

利用上面两个技巧，来推到矩阵分量的反向转换(Backward) 和 正向转换(Forward)

从旧组件L 移动到 新组件， 只需要

核心内在就是 B与F是互逆的！！