• [Machine Learning][Part 5]监督学习——逻辑回归

    目录

    逻辑回归模型理论

    决策边界

    Cost Function : 代价函数

    梯度下降

     计算逻辑回归梯度值：

    计算梯度下降值：

    逻辑回归模型理论

            之前文章中提到监督学习的应用可分为两类：线性回归和逻辑回归。和线性回归不同，逻辑回归输出只有0和1。对于一个逻辑回归任务，可以先使用线性回归来预测y。然而我们希望逻辑回归预测模型输出的是0和1，为了达到这个目的，我们使用sigmoid()来把线性回归预测的输出y映射到0和1之间。

    sigmoid公式为:

     公式中的z表示的是线性回归模型中输出的结果y。m个training data的情况下，y是一个含m个value的向量。

    sigmoid公式代码实现很简单：

    1. def sigmoid(z):
    2.     """
    3.     Compute the sigmoid of z
    5.     Args:
    6.         z (ndarray): A scalar, numpy array of any size.
    8.     Returns:
    9.         g (ndarray): sigmoid(z), with the same shape as z
    11.     """
    12.     g = 1/(1+np.exp(-z))
    13.     return g

    用图形表示sigmod的输出样子是:可以看到输出区间始终在0到1之间，输入z越大，越趋近于1，反之趋近于0

    图一

    逻辑回归的公式与线性回归类似：

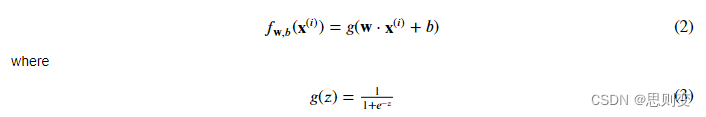
    一句话总结逻辑回归模型：线性回归模型+sigmoid = 逻辑回归模型

    决策边界

    逻辑回归输出的是0和1，由于sigmoid函数是在无穷大的时候趋近于1，无穷小的时候趋近于0,。那么0和1的分界点在哪里，如何判断应当输出0还是应当输出1，这就需要设计一个阈值，来区分开这两种输出。

    现在假设阈值为0.5：

    1. g(z) >=0.5, y=1
    2. g(z)<0.5,    y=0

    那边边界点就在g(z)=0.5。由图一可以看出z=0时，g(z) = 0.5。因此边界点z = 0。而z 是线性回归的输出w*x+b。所以得出w*x+b = 0为分界线，即决策边界。

    下面用一个例子来实现这条决策边界：

    假设有一组training data，每个训练数据包含2个特征值

    1. X = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
    2. y = np.array([0, 0, 0, 1, 1, 1]).reshape(-1,1)
    3.  
    4.  
    5. fig,ax = plt.subplots(1,1,figsize=(4,4))
    6. plot_data(X, y, ax)
    7.  
    8. ax.axis([0, 4, 0, 3.5])
    9. ax.set_ylabel('$x_1$')
    10. ax.set_xlabel('$x_0$')
    11. plt.show()

    分布入下图：

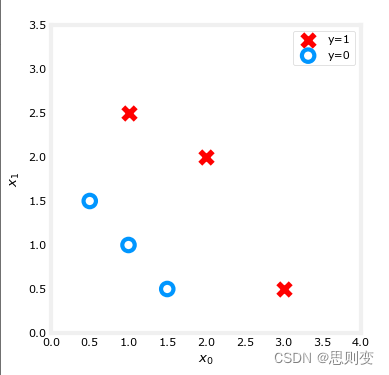
     逻辑回归模型为：

     假设训练完成之后的w_0=1,w_1=1,b=-3。那么这个模型最终公式是：

     这里同样假设:

    1. g(z) >=0.5, y=1
    2. g(z)<0.5,    y=0

    得出来决策边界函数为：

     决策边界图如图二，左下角蓝色部分为y=0，右上角为y=1：

    1. # Choose values between 0 and 6
    2. x0 = np.arange(0,6)
    3.  
    4. x1 = 3 - x0
    5. fig,ax = plt.subplots(1,1,figsize=(5,4))
    6. # Plot the decision boundary
    7. ax.plot(x0,x1, c="b")
    8. ax.axis([0, 4, 0, 3.5])
    9.  
    10. # Fill the region below the line
    11. ax.fill_between(x0,x1, alpha=0.2)
    12.  
    13. # Plot the original data
    14. plot_data(X,y,ax)
    15. ax.set_ylabel(r'$x_1$')
    16. ax.set_xlabel(r'$x_0$')
    17. plt.show()
    图二

    Cost Function : 代价函数

    之前已经实现过线性回归模型的代价函数，那么线性回归的代价模型能不能用到逻辑回归中呢？答案是否定的，因为逻辑回归模型中存在非线性因素，如果直接运用线性模型的代价函数就会出现很多局部最小值，影响最佳w，b组合的寻找。图三中左边是线性回归模型的代价函数，可以看到是凸面的，存在一个最小值，而右图是在逻辑回归模型中应用线性回归的代价函数得到的代价函数结果，可以看到有很多局部最小值，但并非全局最小值。因此线性回归中的代价函数并不能应用到逻辑回归模型中。

    图三
    图三

    因此逻辑回归模型的代价函数使用下面的公式实现：

    代码实现为：

    1. def compute_cost_logistic(X, y, w, b):
    2.     """
    3.     Computes cost
    5.     Args:
    6.       X (ndarray (m,n)): Data, m examples with n features
    7.       y (ndarray (m,)) : target values
    8.       w (ndarray (n,)) : model parameters  
    9.       b (scalar)       : model parameter
    10.       
    11.     Returns:
    12.       cost (scalar): cost
    13.     """
    14.  
    15.     m = X.shape[0]
    16.     cost = 0.0
    17.     for i in range(m):
    18.         z_i = np.dot(X[i],w) + b
    19.         f_wb_i = sigmoid(z_i)
    20.         cost +=  -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)
    21.              
    22.     cost = cost / m
    23.     return cost

    验证一下上面的cost function是否正确：

    1. w_tmp = np.array([1,1])
    2. b_tmp = -3
    3. print(compute_cost_logistic(X_train, y_train, w_tmp, b_tmp))

    输出为：0.36686678640551745

    梯度下降

    梯度下降公式：

     

    对于逻辑回归模型，𝑓𝐰,𝑏(𝑥(𝑖))是预测模型函数，𝑧=𝐰⋅𝐱+𝑏，𝑓𝐰,𝑏(𝑥)=𝑔(𝑧),

     计算逻辑回归梯度值：

    上面公式2和公式3是梯度值的计算公式，首先初始化dj_dw和dj_db，

    计算dj_dw：对于每个训练数据，计算和真实值的误差g(x(i))-y_i，由于训练数据有j个特征值，所以一个训练数据中的j个特征值的误差都要乘以x_j并求和。

    1. def compute_gradient_logistic(X, y, w, b): 
    2.     """
    3.     Computes the gradient for linear regression 
    4.  
    5.     Args:
    6.       X (ndarray (m,n): Data, m examples with n features
    7.       y (ndarray (m,)): target values
    8.       w (ndarray (n,)): model parameters  
    9.       b (scalar)      : model parameter
    10.     Returns
    11.       dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. 
    12.       dj_db (scalar)      : The gradient of the cost w.r.t. the parameter b. 
    13.     """
    14.     m,n = X.shape
    15.     dj_dw = np.zeros((n,))                           #(n,)
    16.     dj_db = 0.
    17.  
    18.     for i in range(m):
    19.         f_wb_i = sigmoid(np.dot(X[i],w) + b)          #(n,)(n,)=scalar
    20.         err_i  = f_wb_i  - y[i]                       #scalar
    21.         for j in range(n):
    22.             dj_dw[j] = dj_dw[j] + err_i * X[i,j]      #scalar
    23.         dj_db = dj_db + err_i
    24.     dj_dw = dj_dw/m                                   #(n,)
    25.     dj_db = dj_db/m                                   #scalar
    26.         
    27.     return dj_db, dj_dw

    计算梯度下降值：

    1. def gradient_descent(X, y, w_in, b_in, alpha, num_iters): 
    2.     """
    3.     Performs batch gradient descent
    4.     
    5.     Args:
    6.       X (ndarray (m,n)   : Data, m examples with n features
    7.       y (ndarray (m,))   : target values
    8.       w_in (ndarray (n,)): Initial values of model parameters  
    9.       b_in (scalar)      : Initial values of model parameter
    10.       alpha (float)      : Learning rate
    11.       num_iters (scalar) : number of iterations to run gradient descent
    12.       
    13.     Returns:
    14.       w (ndarray (n,))   : Updated values of parameters
    15.       b (scalar)         : Updated value of parameter 
    16.     """
    17.     # An array to store cost J and w's at each iteration primarily for graphing later
    18.     J_history = []
    19.     w = copy.deepcopy(w_in)  #avoid modifying global w within function
    20.     b = b_in
    21.     
    22.     for i in range(num_iters):
    23.         # Calculate the gradient and update the parameters
    24.         dj_db, dj_dw = compute_gradient_logistic(X, y, w, b)   
    25.  
    26.         # Update Parameters using w, b, alpha and gradient
    27.         w = w - alpha * dj_dw               
    28.         b = b - alpha * dj_db               
    29.       
    30.         # Save cost J at each iteration
    31.         if i<100000:      # prevent resource exhaustion 
    32.             J_history.append( compute_cost_logistic(X, y, w, b) )
    33.  
    34.         # Print cost every at intervals 10 times or as many iterations if < 10
    35.         if i% math.ceil(num_iters / 10) == 0:
    36.             print(f"Iteration {i:4d}: Cost {J_history[-1]}   ")
    37.         
    38.     return w, b, J_history         #return final w,b and J history for graphing

    梯度下降测试：

    1. w_tmp  = np.zeros_like(X_train[0])
    2. b_tmp  = 0.
    3. alph = 0.1
    4. iters = 10000
    5.  
    6. w_out, b_out, _ = gradient_descent(X_train, y_train, w_tmp, b_tmp, alph, iters) 
    7. print(f"\nupdated parameters: w:{w_out}, b:{b_out}")

    输出：可以看出结果是不断收敛的

    1. Iteration    0: Cost 0.684610468560574   
    2. Iteration 1000: Cost 0.1590977666870457   
    3. Iteration 2000: Cost 0.08460064176930078   
    4. Iteration 3000: Cost 0.05705327279402531   
    5. Iteration 4000: Cost 0.04290759421682   
    6. Iteration 5000: Cost 0.03433847729884557   
    7. Iteration 6000: Cost 0.02860379802212006   
    8. Iteration 7000: Cost 0.02450156960879306   
    9. Iteration 8000: Cost 0.02142370332569295   
    10. Iteration 9000: Cost 0.019030137124109114   
    11.  
    12. updated parameters: w:[5.28 5.08], b:-14.222409982019837

  • 相关阅读:
    Three.JS游戏开发入门
    济南抢注商标与商标在先使用如何认定
    AAOS音频路由 问题分析
    Flex布局和Float布局的实现
    仅30行代码，实现一个搜索引擎(1.0版)
    小程序，公众号绑定微信开放平台帐号-UnionID机制
    计算思维相关书籍 计算机思维、数学思维与逻辑思维
    大数据1星笔试题_220621
    透明质酸改性乳清白蛋白/肌白蛋白/豆清白蛋白/蓖麻蛋白/豌豆白蛋白1b ( PA1b)纳米粒HA-PA1b
    小知识：使用errorstack定位特定问题
  • 原文地址：https://blog.csdn.net/x1987200567/article/details/133789134