力扣第236题 二叉树的最近公共祖先 c++ 递归和回溯 附注释和简短代码

题目

236. 二叉树的最近公共祖先

中等

相关标签

树   深度优先搜索   二叉树

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

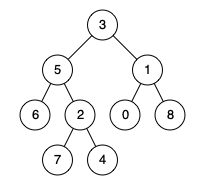
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

思路和解题方法

算法使用递归方法，对每个节点进行遍历。在遍历过程中，首先判断当前节点是否为NULL或等于p或q节点本身，如果是，则返回当前节点。否则，分别递归遍历左右子树，并将其结果保存在left和right变量中。接下来，对left和right进行判断：

• 如果left和right都不为NULL，说明当前节点是p和q的最近公共祖先节点，返回当前节点。
• 如果只有right不为NULL，说明p和q节点都在右子树，返回right节点。
• 如果只有left不为NULL，说明p和q节点都在左子树，返回left节点。
• 如果left和right都为NULL，说明p和q节点都不在当前节点的子树中，返回NULL。

最终返回值即为p和q的最近公共祖先节点。

复杂度

        时间复杂度:

                O(n)

时间复杂度：

• 遍历整棵二叉树的过程中，我们需要访问每个节点一次，因此时间复杂度为O(n)，其中n是二叉树的节点数。

        空间复杂度

                O(n)

空间复杂度：

• 在递归过程中，需要使用递归调用栈来保存每个递归函数的局部变量。在最坏情况下，递归栈的深度等于二叉树的高度。如果二叉树是平衡树，则高度为log(n)，其中n为节点数。如果二叉树是非平衡树，则高度可能达到n，比如链表形式的二叉树。因此，空间复杂度为O(h)，其中h是二叉树的高度。

c++ 代码

class Solution {
public:
    // 递归函数，用于寻找p和q的最近公共祖先节点
    TreeNode* traver(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 如果当前节点为空，返回NULL
        if (root == NULL) {
            return NULL;
        }
        
        // 如果当前节点是p或q本身，则返回当前节点
        if (root == p || root == q) {
            return root;
        }
        
        // 递归遍历左子树，寻找p和q的最近公共祖先节点
        TreeNode* left = traver(root->left, p, q);
        
        // 递归遍历右子树，寻找p和q的最近公共祖先节点
        TreeNode* right = traver(root->right, p, q);
        
        // 根据左右子树的结果进行判断
        if (left != NULL && right != NULL) {
            // 如果左右子树的结果都不为空，说明当前节点是p和q的最近公共祖先节点
            return root;
        }
        else if (left == NULL && right != NULL) {
            // 如果左子树的结果为空，右子树的结果不为空，说明p和q节点都在右子树上
            return right;
        }
        else if (left != NULL && right == NULL) {
            // 如果左子树的结果不为空，右子树的结果为空，说明p和q节点都在左子树上
            return left;
        }
        else {
            // 如果左右子树的结果都为空，说明p和q节点都不在当前节点的子树中
            return NULL;
        }
    }
 
    // 寻找p和q的最近公共祖先节点
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 调用递归函数，返回最近公共祖先节点
        return traver(root, p, q);
    }
};

c++优化后的代码

class Solution {
public:
    // 寻找p和q的最近公共祖先节点
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 如果当前节点为空，或者当前节点是p或q本身，则返回当前节点
        if (root == nullptr || root == p || root == q) {
            return root;
        }
        
        // 递归遍历左子树，寻找p和q的最近公共祖先节点
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        
        // 递归遍历右子树，寻找p和q的最近公共祖先节点
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        
        // 根据左右子树的结果进行判断
        if (left && right) {
            // 如果左右子树的结果都不为空，说明当前节点是p和q的最近公共祖先节点
            return root;
        }
        
        // 如果左子树的结果不为空，则返回左子树的结果
        // 如果左子树的结果为空，右子树的结果不为空，则返回右子树的结果
        return left ? left : right;
    }
};

小代码满足

class Solution {
public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q) {
        if (root == nullptr || root == p || root == q)  return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if (left && right)   return root;
        return left ? left : right;
    }
};

觉得有用的话可以点点赞，支持一下。

如果愿意的话关注一下。会对你有更多的帮助。

每天都会不定时更新哦  >人<  。