计算时间复杂度

时间复杂度与语句被重复执行的次数息息相关。

一、单层循环

单层循环大致可以分为两种，一种是循环体内的语句不影响循环条件的判定。另一种就是循环体内的语句会影响循环条件的判定。

1、循环体内的语句不影响循环条件的判定

这种情况十分常见且简单，比如给数组插入数据。这里不做过多说明。

2、循环体内的语句会影响循环条件的判定

 很明显可以看到，i=i*2会影响i的值，从而影响下一次循环的判定。

我们假设这个语句会循环t次，因为i的初始值为1，所以在循环内i的最终值就是，那么就有。

所以 ,所以答案选D。

二、双层循环

双层循环也可以分为以下两种，

1、内层循环条件与外层循环的变量有关

很明显在内层循环里面的j的判定条件与外层循环变量i的值有关。i的值的范围为从n-1到2，j的值的范围为从1到i-1。于是里面对换的次数应该为：最终结果为，所以答案选D。所以这种情况就是如果内外层有关，那么就是双重求和。

 这里要注意外层循环的操作语句还会影响外层循环的判定。我们现在只看这一层循环，因为执行第一次的时候i为1，即，第二次的时候i的值为2，即。以此类推，假设这层循环执行t次，那么i的最终值应该为，且。并且注意，第t+1次时循环终止，即i的值为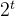。那么肯定就有。

而当i每次对应一个值的时候，内层循环就会执行对应的值的次数。那么总循环次数实际就为。很明显这是一个等比数列，可以得出最终结果为。因为，给不等式两边同时乘以2，那么就有，则有。所以答案选B。

这道题虽然外层循环变量与内层循环条件有关，但是因为i的变化不是线性递增的，它是呈指数级增长的，所以就不能用简单的双重求和来表示。

2、内层循环条件与外层循环的变量无关

在内层循环里面j的判定条件与n有关与外层循环变量i无关，k的范围从1到n，j的范围从1到n。但需要注意的是k的操作语句为。所以外层循环最多执行次。而内层循环执行n次，所以答案选C。所以这种情况就是如果外层不影响内层直接就是两层循环分别算出各自需要的次数然后相乘。