十大排序算法Java实现及时间复杂度

十大排序算法

选择排序

• 原理
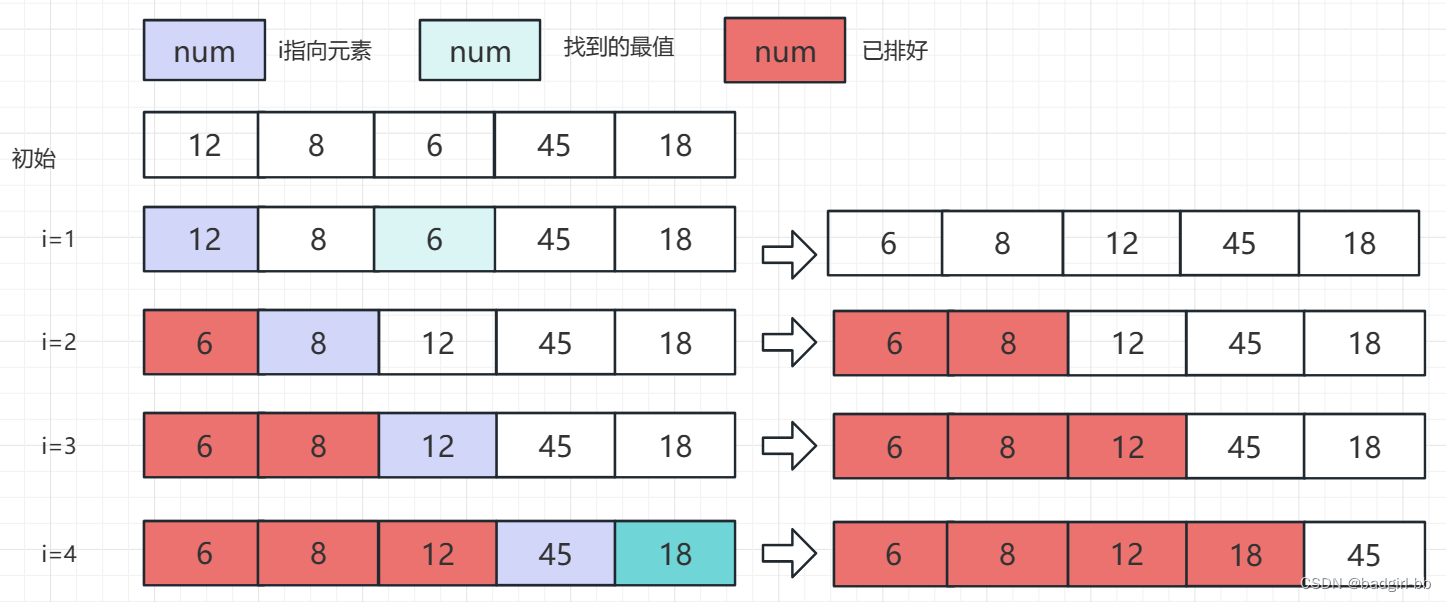
  从待排序的数据元素中找出最小或最大的一个元素，存放在序列的起始位置，
  然后再从剩余的未排序元素中寻找最小/最大元素，放在已排序的序列的末尾，
  以此类推，直到全部待排序的数据元素的个数为零。

• 实现方法

1. 设置下标指针i和j，i从数组的第一个元素开始，j从（i+1）个元素开始
2. j遍历到lens，选出最小的值min，将nums[i]与min交换；如果没有找到一个nums[j]
3. i++开始选取下一个元素，重复2，直到i到达lens-1出
   以数据{12，8，6，45，18}为例

• 图示
  

• 代码实现

public class Sort {
    public static void main(String[] args) {
        int[] nums = {12,8,6,45,18};
        //选择排序
        selectSort(nums);
    }
    public static void selectSort(int[] nums){
        int lens = nums.length;
        int temp;
        //优化，排序之前先遍历
        boolean isSort = true;
        for(int i=0; i < lens-1; ++i){
            if(nums[i] > nums[i+1]){
                //有无序的
                isSort = false;
                break;
            }
        }
        if(isSort){
            return;//直接结束
        }
        //优化结束
        System.out.println("开始选择排序");
        for(int i=0; i< lens-1; ++i){
            for(int j=i+1;j< lens;++j){
                if(nums[j] < nums[i]){
                    temp = nums[j];
                    nums[j] = nums[i];
                    nums[i] = temp;
                }
            }
        }
        for(int i =0; i < lens; ++i){
            System.out.print(nums[i] + " ");
        }

    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

冒泡排序

• 原理
  通过对排序序列从前向后（从下标较小的元素开始）依次比较相邻元素的值，若发现逆序则交换，
  使得值比较大的元素逐渐从前向后移动，就像水底下的气泡一样逐渐向上冒。

• 实现方法

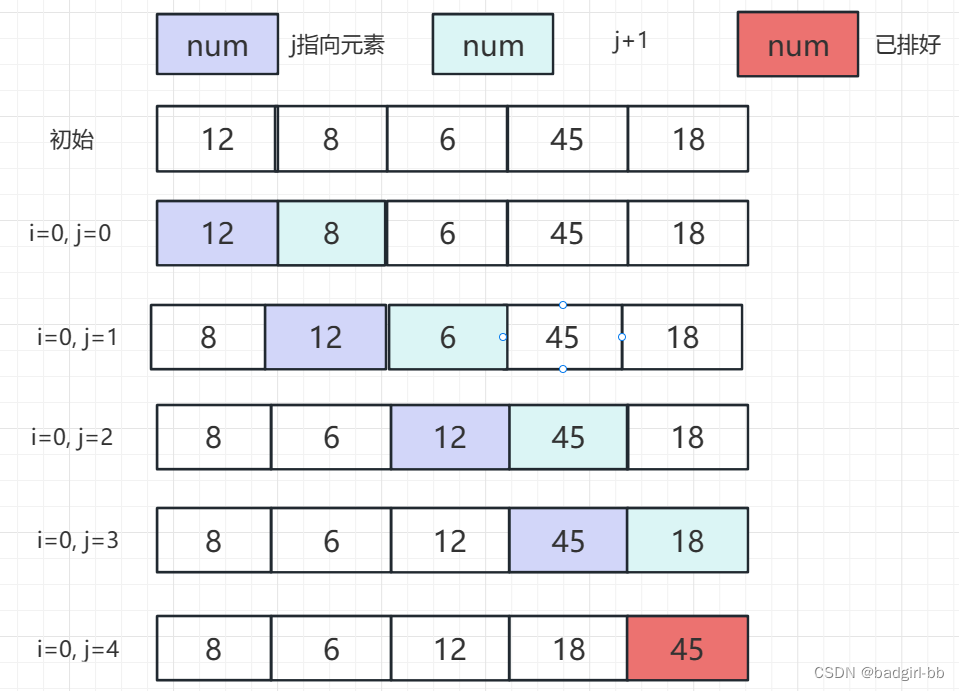
1. 设置下标指针i和j，i用于统计外循环的次数，j用来表示当前轮次需要遍历的元素范围
2. j的范围是0~lens-1-i，因为我们这里是每次将最大的值放在尾部，因此到第i轮的时候，最后i个值已经排完序了，不需要再判断了；
3. 如果nums[j] > nums[j+1],则进行交换
4. 重复上述步骤，直到lens轮排序完毕

• 图示
  

• 代码

public class Sort {
    public static void main(String[] args) {
        int[] nums = {12,8,6,45,18};
        //冒泡排序
        bubbleSort(nums);
    }

    public static void bubbleSort(int[] nums){
        int lens = nums.length;
        int temp;
        System.out.println("开始冒泡排序");
        for(int i=0; i< lens - 1; ++i){
            for(int j = 0; j < lens - 1 - i; ++j){
                if(nums[j] > nums[j + 1]){
                    temp  = nums[j];
                    nums[j] = nums[j + 1];
                    nums[j + 1] = temp;
                }
            }
        }
        for(int i=0;i<lens;++i){
            System.out.print(nums[i] + " ");
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

插入排序

• 原理
  将一个记录插入到有序表中，从而形成一个新的有序表；
  每一步将一个待排序的元素，按照排序码的大小，插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为主。

• 实现过程

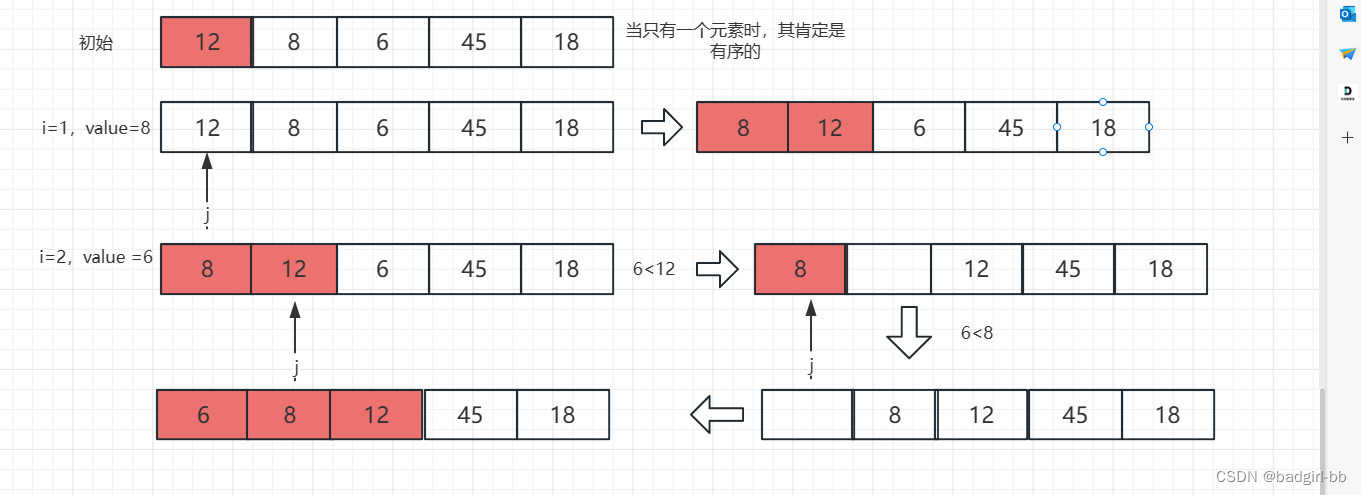
1. 每次从待排序数组中选取元素value，将其插入到有序表中
2. 设置下标指针i和j，i指向待排序元素，j指向已排序元素尾部，并不断左移
3. j=i-1,当j不越界并且value小于nums[j]的时候，我们要将nums[j]及其后面的数组往右边移一位，直到value大于等于nums[j]
4. 此时j+1的位置是value应该插入的位置，将其插入进去即可

• 图示
  

• 代码

public class Sort {
    public static void main(String[] args) {
        int[] nums = {12, 8, 6, 45, 18};
        insertSort(nums);
    }

    public static void insertSort(int[] nums) {
        int lens = nums.length;
        System.out.println("开始插入排序");
        for (int i = 1; i < lens; ++i) {
            int value = nums[i];
            int j;
            for (j = i - 1; j >= 0 && value < nums[j]; j--) {
                nums[j + 1] = nums[j];//挪空位
            }
            nums[j + 1] = value;
        }
        for (int i = 0; i < lens; ++i) {
            System.out.print(nums[i] + " ");
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

希尔排序

• 原理
  先将整个待排序的记录序列分组，对若干子序列分别进行直接插入排序，
  随着增量逐渐减少即整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

• 实现过程
  参考：java希尔排序

• 代码

public class Sort {
    public static void main(String[] args) {
        int[] nums = {12, 8, 6, 45, 18};
        shellSort(nums);
    }

    public static void shellSort(int[] nums) {
        for (int gap = nums.length / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < nums.length; ++i) {
                for (int j = i - gap; j >= 0; j -= gap) {
                    if (nums[j] > nums[j + gap]) {
                        int temp = nums[j];
                        nums[j] = nums[j + gap];
                        nums[j + gap] = temp;
                    }
                }
            }
        }
        System.out.println(Arrays.toString(nums));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

快速排序

• 原理
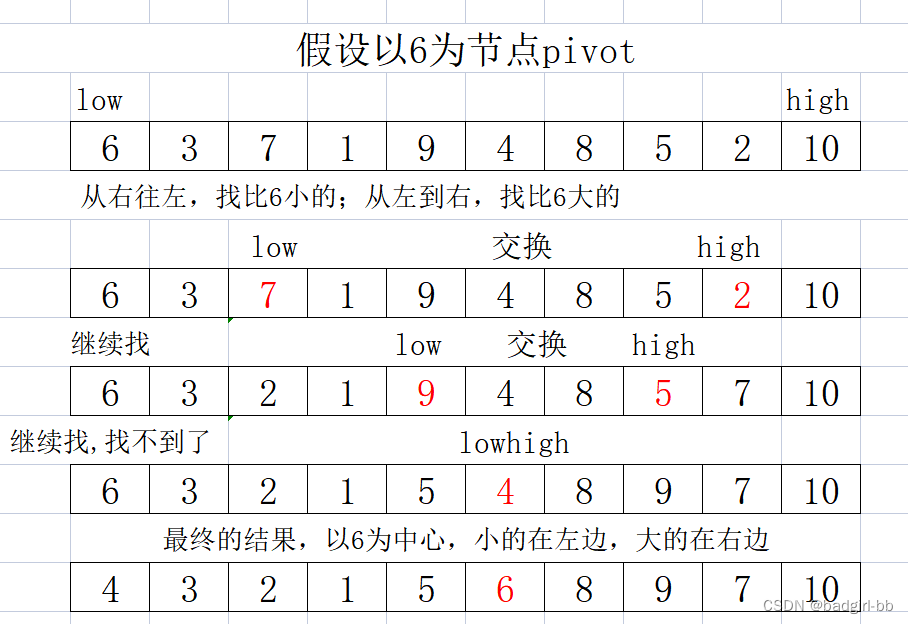
  通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，
  然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

• 图示
  

• 代码

public class Sort {
    static int[] nums = {12, 8, 6, 45, 18};

    public static void main(String[] args) {

        quickSort(nums, 0, nums.length - 1);
        System.out.println("快速排序： " + Arrays.toString(nums));
    }

    public static void quickSort(int[] nums, int low, int high) {
        int i, j, pivot;
        //结束条件
        if (low >= high) {
            return;
        }
        i = low;
        j = high;
        //选择的节点，默认选择第一位数
        pivot = nums[low];
        while (i < j) {
            //从右到左找到第一个比pivot小的数
            while (nums[j] >= pivot && i < j) {
                j--;
            }
            //从左到右找到比节点大的数
            while (nums[i] <= pivot && i < j) {
                i++;
            }
            if (i < j) {
                //循环找到后，交换
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
        //一轮结束后，交换节点的数和ij相遇点的数
        nums[low] = nums[i];
        nums[i] = pivot;
        //对pivot左边和右边的数进行快速排序
        quickSort(nums, low, i - 1);
        quickSort(nums, i + 1, high);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

归并排序

• 原理
  基于分治思想，先将待排序的数组不断拆分，直到拆分到区间里只剩下一个元素的时候。
  不断合并两个有序的子区间，直到所有区间都合并在一起，此时数组有序。

• 实现过程

1. 编写递归函数sortMerge(int[] nums,int left,int right);
2. 参数nums表示要排序的数组，left和right表示当前排序的范围；
3. 每进入一个子函数，计算mid，将待排序数组再一分为二，函数sortMerge的终止条件是left==right，即无法再拆分
4. 回溯时要合并刚刚自己拆分的两个数组，合并的范围同样是left到right，用k表示合并后数组元素对应的下标
5. 此时，两个子区间的合并，就说合并两个有序数组,借助临时数组temp存储还未合并的两个子数组原始的内容
6. 有序数组1的下标用i表示，范围是[left,mid]，有序数组2的下标用j表示，范围是[mid+1,right]
7. 在i，j都未越界的情况下，选择小的存到nums[k],并将对应的指针往右移；
8. 若i/j越界，则将j/i剩下的数据修改到nums中

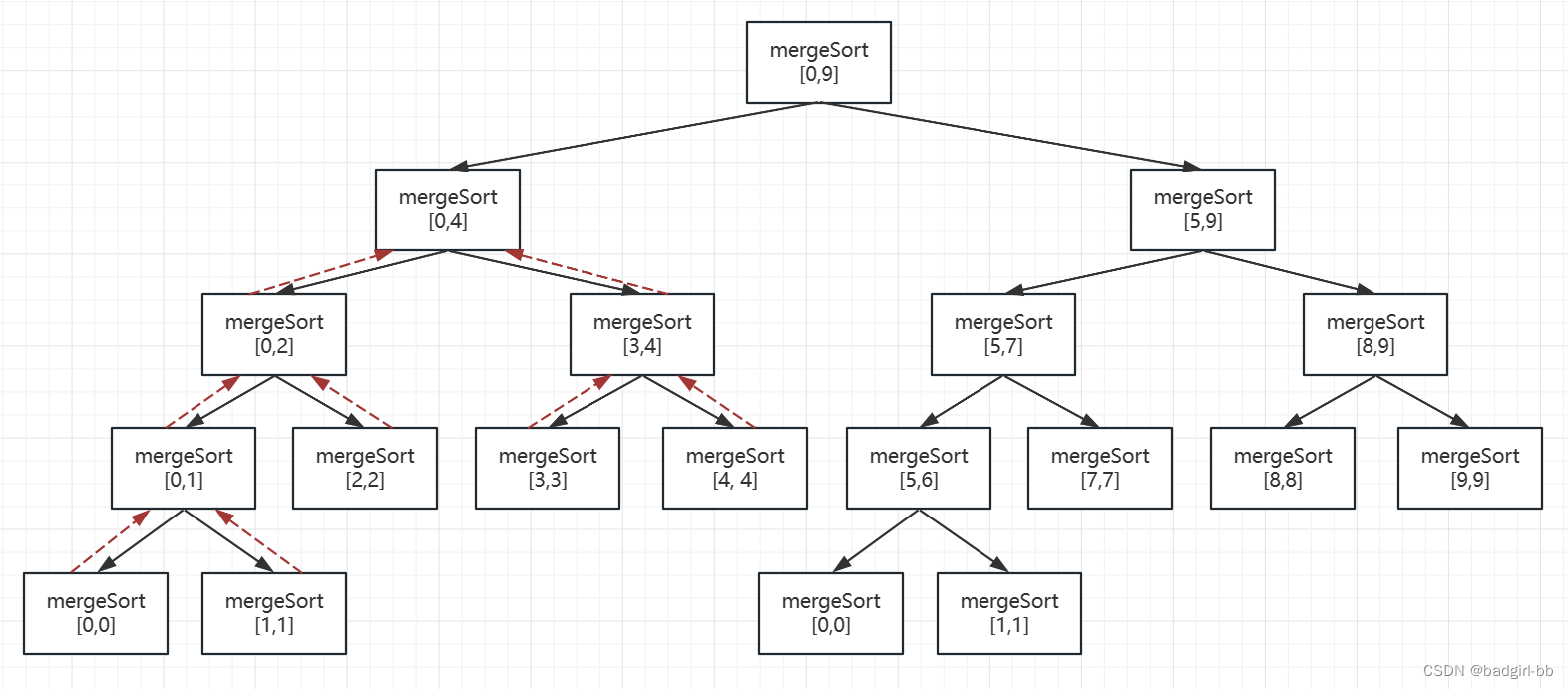
• 图示
  从数组中间拆分，每次拆成两个子区间
  

函数的指向过程就是构造一个二叉树，红色箭头是当递归到left==right时，进行回溯
此时指向函数体里面的合成操作

• 代码

public class Sort {
    public static void main(String[] args) {
        int[] nums = {6, 2, 7, 1, 9, 4, 8, 5, 12, 10};          //给定一个数组
        int len = nums.length;
        int[] temp = new int[len];
        mergeSort(nums, 0, len - 1, temp);
        System.out.println(Arrays.toString(nums)); //打印输出得到数组
    }
    private static void mergeSort(int[] nums, int left, int right, int[] temp) {
        if (left == right) {//当拆分到数组当中只要一个值的时候，结束递归
            return;
        }
        int mid = (left + right) / 2;   //找到下次要拆分的中间值
        mergeSort(nums, left, mid, temp);//记录树左边的
        mergeSort(nums, mid + 1, right, temp);//记录树右边的

        //合并两个区间
        for (int i = left; i <= right; i++) {
            temp[i] = nums[i];
            //temp就是辅助列表，新列表的需要排序的值就是从辅助列表中拿到的
        }
        int i = left;       //左子数组起点
        int j = mid + 1;  //右子数组起点
        //合并两个有序数组，成为一个新的有序数组
        for (int k = left; k <= right; k++) {//k 就为当前要插入的位置
            if (i == mid + 1) { //i到了右子数组起点，证明左子数字已经比较完毕
                nums[k] = temp[j]; //右子数字剩余的全部值赋给原数组
                j++;
            } else if (j == right + 1) { //当j超过当前的数组范围，证明右区间的数组已经遍历完毕了
                nums[k] = temp[i];//如果k还没有走完，证明左区间数据还有剩余，直接全部复制上去
                i++;
            }
            //用来比较，寻找小的哪一位插入
            else if (temp[i] <= temp[j]) { //如果左子数组最小值小于右子数组最小值
                nums[k] = temp[i]; //将两个数组中的最小值赋值给原数组
                i++;
            } else {
                nums[k] = temp[j];
                j++;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

堆排序

• 原理
  堆是一种完全二叉树的数据结构，可以分为大根堆，小根堆。
  大根堆：每个结点的值都大于或者等于他的左右孩子结点的值
  小根堆：每个结点的值都小于或等于其左右孩子的结点值
  以大根堆为例，首先把待排序的元素按照大小在二叉树位置上排列，且要满足堆的特性。
  根据特性把根节点拿出来，然后再堆化下，即用父节点和他的孩子节点进行比较，取最大的孩子节点和其进行交换，
  再把根节点拿出来，一直循环到最后一个节点，就排序好了。

• 实现过程

1. 给定的待排序序列作为二叉树的层序遍历结果，构建二叉树
2. 将这个二叉树构造成一个大顶堆（从最后一个非叶子结点开始，比较它的左右孩子是否比自己大，比自己大就交换，逐层往上找，最后根节点是最大值）
3. 将堆顶元素与末尾元素进行交换，此时末尾为最大值；
4. 将剩余n-1个元素重新构成一个堆，这样会得到n个元素的次小值。如此反复执行，便得到有序序列；

• 图示
  

• 代码

public class Sort {
    static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};
    public static void main(String[] args) {//给定一个数组
        heapSort(nums);
        System.out.println(Arrays.toString(nums)); //打印输出得到数组
    }

    public static void heapSort(int[] nums) {
        System.out.println("开始堆排序");
        //1.构建堆，使得nums[0]成为最大值
        buildMaxHeap(nums);
        for (int i = nums.length - 1; i >= 1; i--) {
            swap(nums, 0, i);//将当前的最大堆顶放在最后一位
            adjustHeap(nums, 0, i);//寻找次大值
        }
    }

    public static void buildMaxHeap(int[] nums) {
        for (int i = (nums.length - 1 - 1) / 2; i >= 0; i--) {
            adjustHeap(nums, i, nums.length);
        }
    }

    public static void adjustHeap(int[] nums, int i, int length) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;
        if (left < length && nums[left] > nums[i]) {
            //左结点大，修改largest下标
            largest = left;
        }
        if (right < length && nums[right] > nums[largest]) {
            //看右节点的值是否会比largest的大
            largest = right;
        }
        if (largest != i) {
            //需要交换
            swap(nums, i, largest);
            adjustHeap(nums, largest, length);//继续调整
        }
    }

    public static void swap(int[] nums, int i, int largest) {
        int temp = nums[i];
        nums[i] = nums[largest];
        nums[largest] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

计数排序

• 原理
  将待排序元素值转换为键存储在额外开辟的数组空间中，其要求输入的数据必须是有确定范围的整数。

• 实现过程
  以待排序元素为0~9以内整数为例
  我们创建一个长度为10的整数ans，ans[i]用于统计数字i在待排序元素中出现的次数
  之后，根据ans[i]的值，输出ans[i]次i，直到遍历完成。

• 图示
  

• 代码

public class Sort {
    static int[] nums = {6, 2, 7, 1, 9, 4, 8, 5, 2, 1, 3, 2, 4, 4, 5, 6, 7};
    public static void main(String[] args) {
        int len = nums.length;
        countSort(nums);
        System.out.println(Arrays.toString(nums)); //打印输出得到数组
    }

    public static void countSort(int[] nums) {
        System.out.println("开始计数排序");
        int len = nums.length;
        int[] a = new int[10];//下标0~9
        for (int i = 0; i < len; ++i) {
            a[nums[i]]++;
        }
        int k = 0;
        for (int i = 0; i < 10; ++i) {
            for (int j = 1; j <= a[i]; j++) {
                nums[k++] = i;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

基数排序

• 原理
  通过键值的部分资讯，将要排序的元素分配至某些桶中；对于一个整数数组，先按个位数从低到高进行排序，相同的放在同一个桶中；
  之后按十位数排序，再按百位数排序，直到所有数的第k位数都是0（K取决于数组中最大的元素）。
• 实现过程

1. 找出数组中的最大值maxNum，遍历轮次与其有关
2. 指针div表示的是当前按哪一个键值进行排序，1，10，100，1000分别表示键值为个位，十位，百位，千位。
3. 每一轮计算元素对应的键值，做法是 nums[i] / div % 10; 如nums[i] = 248,div = 10; nums[i]/div = 248 / 10 = 24,24 %10得到4，
4. 将元素依次装入对应的桶中，每一轮分配完之后，将桶中的数据按顺序依次传回原数组nums中，因为下一轮遍历需要根据此顺序。

• 图示

• 代码

public class Sort {
    static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};
    public static void main(String[] args) {//给定一个数组
        radixSort(nums);
        System.out.println(Arrays.toString(nums)); //打印输出得到数组
    }

    public static void radixSort(int[] nums) {
        System.out.println("开始基数排序");
        //先找到最大值，知道要排序几轮
        int maxNum = Integer.MIN_VALUE;
        for (int i = 0; i < nums.length; ++i) {
            if (nums[i] > maxNum) {
                maxNum = nums[i];
            }
        }
        //创建10个桶，因为桶里面装的数据个数未知，所以用数组+list优于二维数组
        LinkedList<Integer>[] lists = new LinkedList[10];
        for (int i = 0; i < 10; ++i) {
            lists[i] = new LinkedList<>();
        }

        //开始分桶,div表示当前排序的位数，1为个位，10为十位
        for (int div = 1; div <= maxNum; div *= 10) {
            for (int i = 0; i < nums.length; ++i) {
                int num = nums[i] / div % 10;//计算其位数的值
                lists[num].offer(nums[i]);
            }
            //把桶中的数据传回nums数组
            int index = 0;
            for (LinkedList<Integer> list : lists) {
                while (!list.isEmpty()) {
                    nums[index++] = list.poll();
                }
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

桶排序

• 原理
  将序列中的元素分布到一定数量的桶内，然后分别对桶内的元素进行排序与，最后再将各个桶内的有序子序列放回原始序列中。
  对于桶内的元素，可以使用别的排序算法，也可以递归使用桶排序；
  一般桶内元素使用插入算法进行排序。
• 实现过程

1. 找出待排序的数组中的最大元素max和最小元素min
2. 根据指定的桶数创建桶，本文使用的桶是List结构，桶里面的数据也采用List结构存储
3. 根据公式遍历数组元素：桶编号=（数组元素-最小值）*(桶个数-1)/（最大值-最小值），把数据放到相同的桶中
4. 从小到大遍历每一个桶，同时对也桶里的元素进行排序
5. 把排好序的元素从索引为0开始放入，完成排序

• 代码

public class Sort {
    static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};
    public static void main(String[] args) {//给定一个数组
        bucketSort(nums, 3);
        System.out.println(Arrays.toString(nums)); //打印输出得到数组
    }

    public static void bucketSort(int[] nums, int bucketSize) {
        System.out.println("开始桶排序");
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for (int num : nums) {
            max = Math.max(num, max);
            min = Math.min(num, min);
        }
        //创建bucketSize个桶
        List<List<Integer>> bucketList = new ArrayList<>();
        for (int i = 0; i < bucketSize; i++) {
            bucketList.add(new ArrayList<>());
        }
        //将数据放入桶中
        for (int num : nums) {
            //确定桶号：桶编号=（数组元素-最小值）*(桶个数-1)/（最大值-最小值）
            int bucketIndex = (num - min) * (bucketSize - 1) / (max - min);
            List<Integer> list = bucketList.get(bucketIndex);
            list.add(num);
        }
        //对每一个桶进行排序
        for (int i = 0, index = 0; i < bucketList.size(); ++i) {
            List<Integer> list = bucketList.get(i);
            list.sort(null);
            for (int value : list) {
                nums[index++] = value;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

时间复杂度

参考资料

资料1
十大经典排序
快速排序
堆排序
堆排序（Java）
桶排序