669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

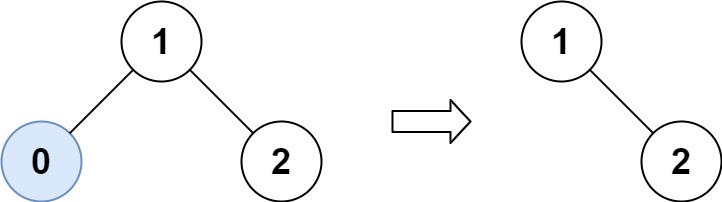
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

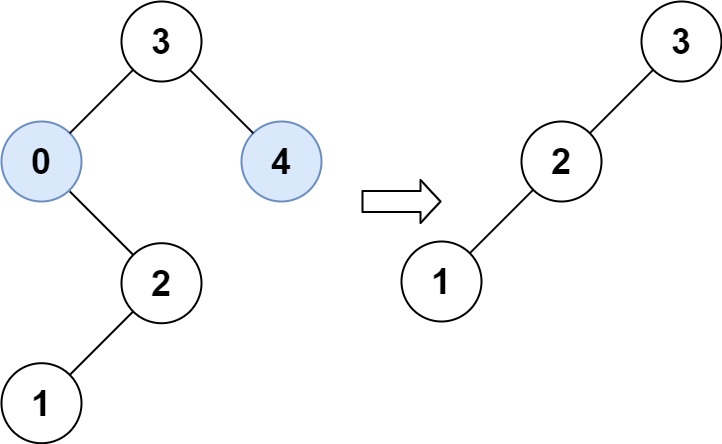
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

class Solution {
public:
    TreeNode* dfs(TreeNode* root,int low,int high){
        if(!root) return nullptr;
        if(root->val < low){
            //遍历到这个不合适的结点，不能停止，得继续看他的右子树
            TreeNode* left = dfs(root->right,low,high);
            return left;
        }
        if(root->val > high){
            //遍历到这个不合适的结点，不能停止，得继续看他的左子树
            TreeNode* right = dfs(root->left,low,high);
            return right;
        }
        //该节点符合，那就遍历左子树，右子树
        root->left = dfs(root->left,low,high);
        root->right = dfs(root->right,low,high);
        return root;
    }
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        return dfs(root,low,high);
    }
};

 

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        //迭代
        //让根节点在合适的位置。
        //让左子树的结点在区间
        //让右子树的节点在区间内
        while(root){
            if(root->val < low){
                root = root->right;
            }
            else if(root->val > high){
                root = root->left;
            }
            else break;
        }
        //root已经满足，处理左子树
        TreeNode* cur = root;
        while(cur){
            if(cur->left && cur->left->val < low){
                cur->left = cur->left->right;
            }
            //可以直接省略，else都是cur = cur->left;
            /*
            else if(cur->left && cur->left > high){
                cur = cur->left;
            }*/
            else cur = cur->left;
        }
 
        cur = root;
        while(cur){
            if(cur->right && cur->right->val > high){
                cur->right = cur->right->left;
            }
            //同理
            /*
            else if(cur->left && cur->left > high){
                cur = cur->left;
            }*/
            else cur = cur->right;
        }
        return root;
    }
};