量化交易全流程（七）

本节目录

资金分配

实盘交易

vn.py框架

我将重点介绍资金分配的基础模型和实现。当然，这里介绍的模型是最基础的模型，现实实践中往往并不能直接使用。因为后续我将加入机器学习和深度学习在量化交易领域中的应用。

现代 / 均值——方差资产组合理论

现代资产组合理论（Modern Portfolio Theory,MPT）是金融理论的重要基础。这一理论是由马克威茨（Harry Markowitz）首先提出的，因为这一理论，马克威茨荣获了1990年的诺贝尔经济学奖。
尽管这种方法早在20世纪50年代就已提出，但时至今日仍然是应用广泛。大量的投资组合理论都衍生于这个基本原理。均值﹣方差理论的核心思想是同时考察资产组合的预期收益和风险。研究当我们有一系列可选资产的时候，应如何对其配置资金权重，从而可以得到最好的收益风险比？本节将简单介绍均值﹣方差的基本理论以及Python的具体实现。

 MPT理论简介： 要实现MPT理论，我们需要做如下几个基本假设。
□ 假设资产的收益率符合正态分布。
□假设资产的预期收益率可以用历史收益率进行估计。
□假设资产的风险可以用资产收益率的方差（标准差）进行估计。
假设有n种资产，资产i的资金分配权重为w，所有资金的权重和为1，也就是：

假设资产i收益率为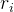，那么组合收益率为：

为了得到组合的预期风险（方差），我们需要先计算协方差矩阵，由各个资产之间协方差组成。

利用投资组合协方差矩阵，我们可以得到投资组合的方差公式：

为了简单起见，我们假定无风险利率，即=0。现在我们可以得到整个组合的夏普比率：

现在我们的目标就是优化权重 w，获得尽可能大的夏普比率，即SR最大。

随机权重的夏普比率

在实际交易中，我们分配资金的对象往往是策略，而不是单纯地持有某种资产。先导入常见的模块，随机选择5只股票的收盘价进行计算得到日收益率，代码如下：

import mysql.connector
import pymysql
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
 
stock_codes = ['000001','000002','000004','000005','000006']
start_date = '20220904'
end_date = '20230904'
dt=pd.DataFrame()
conn=pymysql.connect(host = '127.0.0.1' # 连接名称，默认127.0.0.1
,user = 'root' # 用户名
,password='152617' # 密码
,port= 3306 # 端口，默认为3306
,db='stock_info' # 数据库名称
,charset='utf8' # 字符编码
)
cur = conn.cursor() # 生成游标对象
for stock_code1 in stock_codes:
        sql= "select * from `stocks` where stock_code = " + stock_code1 + " and date > " + start_date + " and date < " + end_date  # SQL语句
        cur.execute(sql) # 执行SQL语句
        data = cur.fetchall() # 通过fetchall方法获得数据
        df = pd.DataFrame(data)
        dt = pd.concat([dt,df],axis=0)
# print(df.head())
cur.close() # 关闭游标
conn.close() # 关闭连接
dt

对数据处理：

dt.columns= ['date','code','open','high','low', 'close','volumes'] # 修改列名
dt = dt[['date','code','close']]
print(dt)
d=dt
# 分组计算收益率
code_grouped = d.groupby('code')
returns = code_grouped['close'].pct_change()
 
# 合并到原始数据中
d['returns'] = returns
d = d.dropna()
print(d)
df_new = d.pivot(index='date', columns='code', values='returns')
df_new.columns=['s1','s2','s4','s5','s6']
print(df_new)
df_new = df_new.astype(float)
df_new.plot()
# 计算年化收益率，假设一年252交易日
df_new.mean() * 252

得到的结果如图：

计算协方差矩阵：

df_new.cov() * 252

下面随机生成一组资金权重：

n=len(df_new.columns)
w=np.random.random(n)
w=w/np.sum(w)

基于这组权重，我们可以得到投资组合的收益率和波动率。这里使用了NumPy的dot函数进行矩阵的乘法，代码如下：

# 投资组合收益率
p_ret= np.sum(df_new.mean()*w)*252
# 投资组合波动率
p_vol=np.sqrt(np.dot(w.T,np.dot(df_new.cov()*252,w)))

以上是针对一组资金权重w得到的收益率和波动率。

现在我们要找出一组权重，这组权重对应着最佳的收益风险比。首先，我们需要随机生成大量的权重，计算对应的投资组合收益率和波动率，进行初步观察，代码如下：

n=len(df_new.columns)
# 保存一系列权重对应的投资组合收益率
p_rets=[]
# 保存一系列权重对应的投资组合波动率
p_vols=[]
# 随机生成10000组权重
for i in range(10000):
    w=np.random.random(n)
    w/=np.sum(w)
    # 投资组合收益率
    p_ret= np.sum(df_new.mean()*w)*252
    # 投资组合波动率（需要注意的是，使用 np 生成的一维数据，实际上是N*1 矩阵，而不是1*N矩阵）
    p_vol=np. sqrt (np.dot (w.T,np.dot (df_new.cov() *252, w)))
    p_rets.append (p_ret)
    p_vols.append (p_vol)
p_rets=np.array (p_rets)
p_vols=np.array (p_vols)

在以上的代码中，我们得到了10000 个随机权重对应的收益率和波动率，现在将其绘制成图，代码如下：

plt.figure(figsize=(10,6))
plt.scatter(p_vols, p_rets, c=p_rets/p_vols,marker='o')
plt.grid(True)
plt.xlabel ('volatility')
plt.ylabel('return')
plt.colorbar (label='Sharpe ratio')

不同权重对应的收益率和波动率（夏普比率）如图所示：

在上图中，x轴对应着波动率，y轴对应着收益率。我们可以观察到，并不是所有的权重都能有良好的表现。对于固定的风险水平（比如0.25)，不同的组合有着不同的收益，同时存在着一个权重，可以有最好的收益（大概是0.23)。作为投资者，最关心的是固定风险水平下收益率的最大化，或者是固定收益率下风险的最小化，也就是所谓的有效边界。

最大化夏普比率

现在我们要找出使投资组合拥有最大夏普比率的资金权重。这是一个包含约束的最优化问题，首先需要建立一个函数，计算组合的夏普比率：

def portfolio_stat(weights):
    '''
    获取投资组合的各种统计值参数：
    weights:分配的资金权重
    返回值：
    P_ret:投资组合的收益率
    P_vol:投资组合的波动率
    P_sr:投资组合的夏普比率
    注意:rets是全局变量,在函数外部定义
    '''
    w = np.array (weights)
    p_ret = np.sum(rets.mean() * w)*252
    P_vol = np.sqrt (np.dot (w.T, np.dot(rets.cov()*252, w)))
    p_sr = p_ret/p_vol
    return np.array([p_ret, p_vol, p_sr])

这里定义了一个函数，输入是权重，输出是收益率、波动率和夏普比率。需要注意的是，函数内部使用的收益率数据rets是全局变量，由外部定义。
下面就来定义优化的目标函数，代码如下：

def min_func_sharpe(weights):
    # 优化的目标函数，最小化夏普比率的负值，即最大化夏普比率
    return -portfolio_stat(weights)[2]

该函数返回了夏普比率的负值，换句话说，我们需要对该函数进行最小化操作。之所以使用这种形式，是因为scipy.optimization 只有 minimize 函数（机器学习中优化目标通常是最小化损失函数）,所以这里使用了这种看起来有点奇怪的形式。
为了进行优化，我们需要使用scipy.optimize模块，代码如下：

import scipy.optimize as sco
# 有n个变量
rets = df_new
n = len(rets.columns)
# 优化的约束条件：资金的权重和为1
cons=({'type':'eq','fun':lambda x:np.sum(x)-1})
bnds=tuple((0,1) for x in range(n))
# 生成初始权重
w_initial = n*[1./n,]
opts_sharpe = sco.minimize(min_func_sharpe, w_initial, method='SLSQP',bounds=bnds,constraints=cons)
opts_sharpe

最后的 opts_sharpe 就是我们优化的结果。


查看message 我们知道已成功优化。fun对应着优化后的函数值，也就是说，夏普比率为-3.1（有点惊人），对应的权重就是x的值。示例代码如下：

opts_sharpe['x'].round(2)

输出结果如下：

可以看到,除了s4权重为1，其他的都是0。这很明显，因为有三个策略的预期收益率是负值，权重置为0当然是最好的选择，s4和s6相比当然是把所有权重都给s4。

Black-Litterman 资金分配模型

MPT的优化矩阵算法

前面讲述了最大化夏普比率的具体操作流程，但仍有几个问题尚待解决。
为什么最大化夏普比率所带来的投资组合就是最优资金分配，最优的含义是什么？
即使最大化夏普比率所得到的组合的确是最优的，那么在生成的有效边界（efficient frontier）上是否还存在其他的投资组合收益，使得其风险收益比优于最大化夏普比率所带来的投资组合？
另外，投资者的效用函数是异质性的，那么最大化夏普比率对投资者的效用函数是否具有异质性表现。

第一个问题的实质是，我们优化的目标函数在经济学意义上究竟是指什么？第二个问题的实质是我们所解的目标函数针对资产权重的函数凹凸性？前两个问题通过代数代换即可理解，第三个问题的实质则相对比较复杂。
我们先来看第一个问题。先给出一个发现，具体如下。
对于任意一个"风险"资金分配组合，其市场"期望收益率"(expected rate of return)最大化的权重分配，等同于解决如下夏普率最大化问题：

maxw=E(Rp)−RFδpmaxw=E(Rp)−RFδp             ;s.t.w′l=1s.t.w′l=1

证明：对于任意的资金分配组合，我们可以将其拆分为风险子投资组合和无风险子投资组合。其期望的收益率为：

E(Rp)=wE(ra)+(1−w)E(rf)E(Rp)=wE(ra)+(1−w)E(rf)

其风险仅与其中的风险子投资组合有关：δp=wδaδp=wδa

通过代数整理，可以得到：

E(Rp)=rf+δpδaE(ra−rf)E(Rp)=rf+δpδaE(ra−rf)

可以发现的是，实质上任意资金分配组合的期望收益率与构成其组合的风险子组合是呈线性相关的，我们可以将该曲线画出，所画的曲线称为（CAL资金分配线，Capital Allocation Line)，其代表的含义是对于每一单位的投资组合风险，其期望收益所需要的补偿为夏普率单位的期望收益。我们可以发现，随着夏普率的升高，CAL的斜率升高，投资组合单位风险得到的期望收益也就越高。至此,第一个问题可以得到解答。最大化风险资产组合的夏普比率（即每一个组成资产的夏普比率，因为夏普比率是一个线性函数。）能够提高整体资金分配的单位风险回报率，因而需要最大化夏普比率。
再来看第二个问题，我们可以证明，有效边界（efficient frontier）实际上是一个全局凹函数（concave function)。其凹性使得我们的资金分配线能够切于有效边界产生一个最优的夏普比率市场投资组合，这根切线即称为资本市场线CML（capital market line)。
第三个问题，有了前面的铺垫，我们现在可以画出如图所示的图像:

可以看到，在CML上面，投资者通过添加或减少无风险资金成本的杠杆，可以获得相对于有效边界上，风险﹣收益权衡更优的投资组合。而风险承受能力的大小，或者说在资本充裕的情况下，投资者的风险厌恶程度，决定了其投资组合的无风险资产占比，而风险资产的各项组成中资产的比重是恒定不变的。然而，前提是假设市场上"所有的"投资者均为风险厌恶类型，即资产收益率的上下波动会给投资者带来负效用。显然，假设风险厌恶型会带来数学上的很多便利；另外，MPT还有一个更为重要的假设，所有的投资者不但全是风险厌恶型，而且所拥有的信息也是完全同质化的，即所有的投资者拥有相同的信息库，资本操作的空间也是完全一样的，买进卖空都受同样的限制，没有私有信息。在真实世界的情况中，投资者的属性往往要复杂得多，这也使得该模型仅在理论上非常有洞察力，但实际表现却不尽如人意。

了解了 MPT 背后的数学、经济学逻辑之后，我们就可以着手用矩阵运算的方式来更高效地解决资金分配的问题了，同时，也可以对该模型做出一定的修正。

对于之前提到的夏普率最大化的规划问题最终的closed form solution结果如下：

w∗=(∑)−1μ​l′(∑)−1μw∗=(∑)−1μ​l′(∑)−1μ

其中，u为各项组成资产的风险溢价收益，∑为溢价收益协方差矩阵。实现代码具体如下：

首先随机取出100只股票代码:

import pandas as pd
import numpy as np
from numpy.linalg import inv
import mysql.connector
import pymysql
import matplotlib.pyplot as plt
import random
import tushare as ts
 
random.seed(123)  # 设置随机数种子为123
pro = ts.pro_api('fdf059e3fd18ba53290c4907562f871fc598b37ac78f2536859003f3')
#查询当前所有正常上市交易的股票列表
#您每小时最多访问该接口1次
data = pro.query('stock_basic', exchange='', list_status='L', fields='ts_code,symbol,name,area,industry,list_date')
 
# 创建随机整数序列,不要把范围弄太大，随机生成去取数据，好多都是新股没有历史数据
s = [random.randint(1, 2000) for _ in range(100)]
 
# s=list(range(101))
# 使用s作为df的行索引提取数据
result = data.loc[s]
 
result = result[['symbol']]
result = result.sort_values('symbol')
print(result)

stock_codes = list(result['symbol']) # 转换成列表

从数据库拉取数据： 

# 读取数据
# stock_codes = ['000001','000002','000004','000005','000006']
start_date = '20220304'
end_date = '20230904'
dt=pd.DataFrame()
conn=pymysql.connect(host = '127.0.0.1' # 连接名称，默认127.0.0.1
,user = 'root' # 用户名
,password='152617' # 密码
,port= 3306 # 端口，默认为3306
,db='stock_info' # 数据库名称
,charset='utf8' # 字符编码
)
cur = conn.cursor() # 生成游标对象
for stock_code1 in stock_codes:
        sql= "select * from `stocks` where stock_code = " + stock_code1 + " and date > " + start_date + " and date < " + end_date  # SQL语句
        cur.execute(sql) # 执行SQL语句
        data = cur.fetchall() # 通过fetchall方法获得数据
        df = pd.DataFrame(data)
        dt = pd.concat([dt,df],axis=0)
# print(df.head())
cur.close() # 关闭游标
conn.close() # 关闭连接
 
dt.columns= ['date','code','open','high','low', 'close','volumes'] # 修改列名

备份操作： 

risk_stock = dt
risk_stock

拉取无风险收益率：首先存放在数据库格式如下：

# 读取无风险收益
start_date = '20220304'
end_date = '20230904'
dt=pd.DataFrame()
conn=pymysql.connect(host = '127.0.0.1' # 连接名称，默认127.0.0.1
,user = 'root' # 用户名
,password='152617' # 密码
,port= 3306 # 端口，默认为3306
,db='stock_info' # 数据库名称
,charset='utf8' # 字符编码
)
cur = conn.cursor() # 生成游标对象
if True:
        sql= "select * from `shibor` where" + " date > " + start_date + " and date < " + end_date  # SQL语句
        cur.execute(sql) # 执行SQL语句
        data = cur.fetchall() # 通过fetchall方法获得数据
        df = pd.DataFrame(data)
        dt = pd.concat([dt,df],axis=0)
# print(df.head())
cur.close() # 关闭游标
conn.close() # 关闭连接
rf = dt
rf.columns=['date','type','ot','1w', '2w', '1m', '3m', '6m', '9m','1y']
rf.head(5)

统一时间：

 
# 统一index
rf['date']= [pd.Timestamp(x) for x in rf['date'].tolist()]
rf=rf.set_index('date')
rf

提取需要的时间段和类型：

rf= rf[rf['type'] == '5_day_mean']
rf= rf[rf.index >= '2022-08-15']
rf= rf[rf.index <= '2023-09-01']
rf

清洗股票数据：

# 清洗数据
# 去掉无用的数据，并且将日期作为 index
risky=risk_stock
risky=risky[['date','code','close']]
risky = risky.groupby(['date', 'code']).sum()
# 将每个日期的数据转化为列
risky = risky.reset_index().pivot(index='date', columns='code', values='close')
risky

 数据转换（因为在数据库里面是dicimal，在这里处理要转换成float）:

# 全部转化为浮点数运算
for c in risky.columns.tolist():
    risky[c]=risky[c].map(float)
for c in rf.columns.tolist()[2:]:
    rf[c]=rf[c].map(float)/100

risky

rf

 可运行部分：（# 筛掉数据量太小的股票（数据量太小对协方差矩阵的估计会造成很大的影响））

也可以不运行

# 筛掉数据量太小的股票（数据量太小对协方差矩阵的估计会造成很大的影响）
def filter_stocks(df, top):
    out = pd.DataFrame()
    data_amount_order = {}
    for stock in df.columns.tolist():
        lenc = len(df[stock].dropna())
        data_amount_order[stock] = lenc
    data_amount_order = sorted(data_amount_order.items(), key=lambda x: x[1], reverse=True)
    data_to_use = [stock[0] for stock in data_amount_order[:top]]
    for stock in data_to_use:
        out[stock] = df[stock]
    out = out[(len(df) - data_amount_order[top-1][1]):]
    return out
 
top = 99
risky = filter_stocks(risky, top) # 99列

注意日期索引格式转换 

risky.index = pd.to_datetime(risky.index)
rf.index = pd.to_datetime(rf.index)

 以下是计算代码：得到分配权重、协方差等结果

# 可以指定不同的计算频率
freq='1m'
class CapitalAllocator():
    def __init__(self,rf,risky,freq):
        self.rf = rf
        self.freq = freq
        self.risky = risky
    
    def freq_coef(self):
        if 'm' in self.freq:
            time_coef=30
        elif 'y' in self.freq:
            time_coef=365
        elif'w' in self.freq:
            time_coef=7
        else:
            time_coef=1
        if 'o' in self.freq:
            return 1
        else:
            return int(freq[0]) * time_coef
        
    def get_expected_excessive_return(self):
        risky=self.risky.copy()
        print(risky)
        risky = risky.resample(self.freq,convention = 'end').fillna("ffill")
        risky_return = risky.pct_change()
        portfolio = risky_return.copy()
        # portfolio=portfolio.dropna()
        print(portfolio)
        # print(portfolio.index.duplicated()) # 检查数据中是否存在重复的索引标签
        
        portfolio = portfolio[~portfolio.index.duplicated()] #删除重复的行
        # excessive_return = excessive_return.groupby(level=0).mean() # 将重复的行合并成一个
 
        portfolio['risk_free'] = self.rf[self.freq] *(self.freq_coef()/365)
 
        portfolio.dropna(inplace =True)
 
        excessive_return = pd.DataFrame()
        for c in risky.columns.tolist():
            excessive_return[c] = portfolio[c] - portfolio['risk_free']
        return excessive_return * (365.0/self.freq_coef()) # 取年化收益率
    
    def get_varcov(self):
        excessive_return = self.get_expected_excessive_return()
        varcov= excessive_return.cov()
        return varcov
    
    def general_markowitz(self):
        excessive_return = self.get_expected_excessive_return()
        varcov = self.get_varcov()
        expected_excessive_return = excessive_return.mean()*(self.freq_coef()/365)
 
        # 利用矩阵公式直接计算权重
        weight = np.matmul(inv(varcov.values), np.array (expected_excessive_return.tolist()))/np.matmul(np.matmul(np.ones((1, top)), inv(varcov.values)), np.array(expected_excessive_return.tolist()))
        return dict (zip(excessive_return.columns.tolist(),weight) ), weight, np.matmul(weight,expected_excessive_return),varcov
 
allocator = CapitalAllocator (rf, risky, freq)
 
# 获得资金分配权重
allocation,weight,er,varcov = allocator.general_markowitz()

最终得到的部分结果如图所示：

weight

肯定已经发现，这个投资组和的权重十分疯狂，在A股市场下是完全不可能实现的，卖空限制以及杠杆限制使得整体的资金分配变得不可能。虽然我们可以加一些限制来使得整体的投资组合权重满足监管要求，但这样一来就有可能导致 closed form solution 不能计算出来。而且，更为重要的是，MPT 框架下的资产权重分配一个很不稳定的系统——只要构成资产组合的某些资产有些许变动，都会对整体的资金分配造成很大的影响，这一点从closed form solution里的协方差矩阵便可看出端倪。
另外一个问题是股票数据本身噪音比较大，市场敏感度较高，其收益相关性会非常高，这就会造成协方差估计矩阵的逆会变得非常不稳定。这个问题实际上很难得到解决，一个妥协的方案是仅选取其中交易历史较长的股票，期望在大规模数据的情况下能够将这种"多重线性相关性"的影响降低。但其始终只是一个妥协产物。

B-L模型：

前面关于MPT的实践中，我们提到MPT 模型的假设非常理想化，现实世界的复杂性难以被完全表现出来。所有投资者拥有相同的信息这个假设只是在数学上能够提供便利，但实际上并没有任何作用。特别是对于主动投资型选手而言，这一资金分配理论完全与其哲学背道而驰。另外，MPT计算出来的权重非常的疯狂，并且容易受个别资产的收益浮动而使得整个系统不稳定。为了解决这些问题，Black-Litterman基于贝叶斯框架得出了另外一套解决方案。
BL 模型的基本思想是：假定我们从交易所指数公布公告里获取的市场指数权重已经是最优的了，在这一假设情况下，我们会得出一个先验权重，即市场投资组合权重。在先验权重的前提下，如果有异质化信息，即通过公开信息分析所得出的有别于其他投资者的信息，并且符合投资者个人的风险偏好，那么将这一信息整合进资产风险溢价内，可以得到一个后验权重。
数学上的表述如下。
假定先验市场权重由如下规划问题得出：

argmaxww′∏−λ2w′∑wargmaxww′∏−λ2w′∑w

投资者基于先验权重，以及本身的异质化信息：

P′μ=Q+ξ

获得资产风险溢价收益的后验分布：

E(Rposterior)∼N(ˆμ,ˆ∑)

投资者求解后验权重规划：

argmaxww′ˆμ−λ2w′ˆ∑w

得到的最终结果为：

ˆμ=[(ι∑)−1+P′Ω−1P]−1[(ι∑)−1ρ∏+P′Ω−1Q]

ˆM−1=[(ι∑)−1+P′Ω−1P]−1

ˆ∑=∑+ˆM−1

wposterior=ˆ∑−1λˆμ

用代码实现上述推导：

提取上面的代码和权重：（用该权重计算得到权重是BL权重的逆）

# Black-Litterman Model
# 交易所公布的指数权重
ist = pd.DataFrame(weight)
st = pd.DataFrame(risky.columns)
market_equilibrium = pd.concat([st,ist],axis=1)
market_equilibrium.columns = ['stock_id','weight']
market_equilibrium

 # 筛选历史区间相对较长的股票池，定义一些变量：

# 筛选历史区间相对较长的股票池
# market_equilibrium = market_equilibrium[market_equilibrium('stock_id').isin(risky.columns.tolist())]
market_equilibrium['weight'] = [x/sum(market_equilibrium['weight']) for x in market_equilibrium['weight']]
market_equilibrium_weight = (market_equilibrium.set_index(['stock_id'])).T
# 风险厌恶程度
risk_aversion = 1
varcov = allocator.get_varcov() # 计算的是值
# print(varcov)
equilibrium_excess_return = risk_aversion * np.dot(varcov, market_equilibrium_weight.T)
 
# 个人观点的不确定性，我们假定其与风险收益协方差成正比
tao = 0.05

 全部观点数据和计算代码：

# 定义观点数据结构
class View():
    def __init__(self, outperform):
        self.outperform = outperform
 
# 绝对观点：某个子投资组合的收益预期为 x %
class AbsoluteView(View):
    def __init__(self,portfolio, outperform):
        super(AbsoluteView,self).__init__(outperform)
        self.portfolio = portfolio
 
# 相对观点：A子投资组合的收益比B投资组合收益高（低）x %
class RelativeView(View):
    def __init__(self,better_portfolio,worse_portfolio, outperform):
        super(RelativeView,self).__init__(outperform) # 构造有用的函数，里面的初始化变量
        self.better_portfolio = better_portfolio
        self.worse_portfolio = worse_portfolio
 
def generate_view_vector(view, assets_horizon):
    # view是上述流程定义的类
    # assets_horizon是当前投资者的资产空间
    if isinstance(view, AbsoluteView):
        view_vector = view.portfolio.copy()
        for asset_code in assets_horizon:
            if asset_code not in view.portfolio.keys():
                view_vector[asset_code] = 0
        return view_vector
    
    elif isinstance(view,RelativeView):
        view_vector = {}
        for asset_code in assets_horizon:
            if asset_code in view.better_portfolio.keys():
                view_vector[asset_code] = view.better_portfolio[asset_code]
            elif asset_code in view.worse_portfolio.keys():
                view_vector[asset_code] = -view.worse_portfolio[asset_code]
            else:
                view_vector[asset_code] = 0
        return view_vector
        
def generate_view_matrix(views,assets_horizon):
    view_records = []
    outperformance = []
    for view in views:
        view_records.append(generate_view_vector(view, assets_horizon))
        outperformance.append(view.outperform)
    view_matrix = pd.DataFrame.from_records(view_records)
    outperformance = np.array(outperformance)
    outperformance.shape = (len(views),1)
    return view_matrix,outperformance
 
# 假设000006比000019股票收益率高2%
b_view = RelativeView({'000006':1},{'000019':1},0.02)
 
view_matrix, outperformance = generate_view_matrix([b_view], market_equilibrium_weight.columns.tolist())
 
def diagonalize(matrix):
    eigen= np.linalg.eig(matrix)
    accompany= eigen[1]
    diag=np.dot(np.dot(inv(accompany), matrix), accompany)
    return diag
 
omega = diagonalize(np.dot(np.dot(view_matrix, tao * varcov), view_matrix.T))
interimM = inv(inv(tao * varcov) + np.dot(np.dot(view_matrix.T, inv(omega)), view_matrix))
right_part = np.dot(inv(tao * varcov), equilibrium_excess_return) + np.dot(np.dot(view_matrix.T, inv(omega)), outperformance)
 
# 通过公式计算
posterior_expected_excess_return = np.dot(interimM, right_part)
posterior_varcov = varcov + interimM
posterior_weight = 1 / risk_aversion * np.dot(inv(posterior_varcov), posterior_expected_excess_return)
posterior_portfolio_excess_return = np.dot (posterior_expected_excess_return.T, posterior_weight)
posterior_portfolio_excess_return # 预期收益为负
posterior_varcov # 协方差矩阵
posterior_expected_excess_return # 每只股票的超额收益
1/posterior_weight

最后的权重如图所示：

实现的收益率为：

由上图可以看到，且权重在A股市场上有问题。但可以整个流程看到，Black-Litterman弥补了MPT框架下的许多不足之处，加入了认为的情绪化新的观点。

------------------------------------------------------B-L Model另一种形式------------------------------------------

Markowitz模型输入参数包括历史数据法和情景分析法两种方法,情景分析法的缺点是主观因素,随意性太强,因此使用历史数据法, 将资产的均值和协方差输入模型是比较常见的作法. 不过, 不足之处很明显: 未来的资产收益率分布不一定与过去相同. 此外, Markowitz 模型结果对输入参数过于敏感.

Black-Litterman模型就是基于此的改进. 其核心思想是将投资者对大类资产的观点 (主观观点) 与市场均衡收益率 (先验预期收益率)相结合,从而形成新的预期收益率(后验预期收益率). 这里的先验预期收益率的分布可以是贝叶斯推断中的先验概率密度函数的多元正态分布形式,投资者的主观观点就是贝叶斯推断中的似然函数(可以看作新的信息, 因为做出主观判断必然是从外界获取得到了这些资产的收益率变化信息), 而相应的, 后验预期收益率也可以从后验概率密度函数中得到。

BL模型的求解步骤包括下面几步:

(1) 使用历史数据估计预期收益率的协方差矩阵作为先验概率密度函数的协方差.

(2) 确定市场预期之收益率向量, 也就是先验预期收益之期望值. 作为先验概率密度函数的均值. 或者使用现有的期望值和方差来反推市场隐含的均衡收益率(Implied Equilibrium Return Vector), 不过在使用这种方法时, 需要知道无风险收益率Rf的大小.

(3) 融合投资人的个人观点,即根据历史数据(看法变量的方差)和个人看法(看法向量的均值)

(4) 修正后验收益:

ˆμ=[(ι∑)−1+P′Ω−1P]−1[(ι∑)−1ρ∏+P′Ω−1Q]

ˆM−1=[(ι∑)−1+P′Ω−1P]−1

(5) 投资组合优化: 将修正后的期望值与协方差矩阵即$\mu^{BL}, \Sigma^{BL} $重新代入Markowitz投资组合模型求解.

代码实现：

(1)定义求解函数,输入为投资者观点P,Q以及目前资产的市场收益率矩阵,输出为后验的市场收益率和协方差矩阵.

import numpy as np
import baostock as bs
import pandas as pd
from numpy import  linalg
def blacklitterman(returns,tau,P,Q):
    mu = returns.mean()
    sigma = returns.cov()
    pil = np.expand_dims(mu,axis = 0).T
    ts = tau * sigma
    ts_1 = linalg.inv(ts)
    Omega = np.dot(np.dot(P,ts), P.T)* np.eye(Q.shape[0])
    Omega_1 = linalg.inv(Omega)
    er = np.dot(linalg.inv(ts_1 + np.dot(np.dot(P.T,Omega_1),P)),(np.dot(ts_1 ,pil)+np.dot(np.dot(P.T,Omega_1),Q)))
    posterirorSigma = linalg.inv(ts_1 + np.dot(np.dot(P.T,Omega_1),P))
    return [er, posterirorSigma]

(2) 实列分析
我们选取五支股票: 白云机场, 福建高速, 华夏银行, 生益科技和浙能电力. 假设现在分析师的观点为:

白云机场, 华夏银行, 浙能电力, 生益科技四只股票的日均收益率均值为0.3%
白云机场和福建高速的日均收益率均值高于浙能电力0.1%
则投资者观点矩阵P为:

Q为：

则获取后验收益率和协方差的代码为:
 

pick1 = np.array([1,0,1,1,1])
q1 = np.array([0.003*4])
pick2 = np.array([0.5,0.5,0,0,-1])
q2 = np.array([0.001])
P = np.array([pick1,pick2])
Q = np.array([q1,q2])

获取股票数据, 并且获得后验的均值和方差:

def get_stock_data(t1,t2,stock_name):
    lg = bs.login()
    print('login respond error_code:' + lg.error_code)
    print('login respond  error_msg:' + lg.error_msg)
 
    #### 获取沪深A股历史K线数据 ####
    # 详细指标参数，参见“历史行情指标参数”章节
    rs = bs.query_history_k_data(stock_name,
                                 "date,code,open,high,low,close,preclose,volume,amount,adjustflag,turn,tradestatus,pctChg,isST",
                                 start_date=t1, end_date=t2,
                                 frequency="d", adjustflag="3")
    print('query_history_k_data respond error_code:' + rs.error_code)
    print('query_history_k_data respond  error_msg:' + rs.error_msg)
 
    #### 打印结果集 ####
    data_list = []
    while (rs.error_code == '0') & rs.next():
        # 获取一条记录，将记录合并在一起
        data_list.append(rs.get_row_data())
    result = pd.DataFrame(data_list, columns=rs.fields)
    print(result)
 
    #### 结果集输出到csv文件 ####
    result.to_csv(r"C:\Users\59980\Desktop\peixun\zong\history_A_stock_k_data.csv", index=False)
    print(result)
 
    #### 登出系统 ####
    bs.logout()
    result['date'] = pd.to_datetime(result['date'])
    result.set_index("date", inplace=True)
    return result
 
byjc = get_stock_data('2014-1-1','2015-1-1','sh.600004')
hxyh = get_stock_data('2014-1-1','2015-1-1','sh.600015')
zndl = get_stock_data('2014-1-1','2015-1-1','sh.600023')
fjgs = get_stock_data('2014-1-1','2015-1-1','sh.600033')
sykj = get_stock_data('2014-1-1','2015-1-1','sh.600183')
 
 
by = byjc['pctChg']
by.name = 'byjc'
by = pd.DataFrame(by,dtype=np.float32)/100
 
 
hx = hxyh['pctChg']
hx.name = 'hxyh'
hx = pd.DataFrame(hx,dtype=np.float32)/100
 
zn = zndl['pctChg']
zn.name = 'zndl'
zn = pd.DataFrame(zn,dtype=np.float32)/100
 
fj = fjgs['pctChg']
fj.name = 'fjgs'
fj = pd.DataFrame(fj,dtype=np.float32)/100
 
sy = sykj['pctChg']
sy.name = 'sykj'
sy = pd.DataFrame(sy,dtype=np.float32)/100
 
sh_return = pd.concat([by,fj,hx,sy,zn],axis=1)
res = blacklitterman(sh_return,0.1,P,Q)
p_mean = pd.DataFrame(res[0],index = sh_return.columns, columns = ['posterior_mean'])
p_cov = res[1]
print(p_mean)
print(p_cov)

结果如图：

 这时候,已经可以使用Markowitz模型进行资产的配置. 定义新的函数blminVar以求解资产配置权重. 该函数的输入变量为blacklitterman函数的输出结果, 以及投资人的目标收益率goalRet.假设目标收益率为年化70%,则goalRet = 0.7:

def blminVar(blres, goalRet):
    covs = np.array(blres[1])
    means = np.array(blres[0])
    L1 = np.append(np.append(covs.swapaxes(0,1),[means.flatten()],axis=0),[np.ones(len(means))],axis=0).swapaxes(0,1)
 
    L2 = list(np.ones(len(means)))
    L2.extend([0,0])
    L3 = list(means)
    L3 = [float(a) for sub_arr in L3 for a in sub_arr]
    L3.extend([0,0])
    L4 = np.array([L2,L3])
    L = np.append(L1,L4,axis=0)
    results = linalg.solve(L,np.append(np.zeros(len(means)),[1,goalRet]))
 
    return pd.DataFrame(results[:-2],columns = ['p_weight'])
 
blresult = blminVar(res,0.70/252)
print(blresult)

得到最终权重为：

实盘交易

当我们完成了策略的研发工作之后，就需要进行实盘交易了。对于日线级别的策略来说，手动下单其实也是可行的。手动下单对于品种不是很多，频率不是很高的策略来说，当然是一种简便易行的方式。但是在量化策略中，品种往往很多，交易频率有时也很高，手动下单几乎不可能（除非招募很多交易员）。这时我们就需要利用计算机自动下单。
要实现自动交易有两种方式，一种是使用现成的第三方交易平台。一般来说，第三方平台语法简单、文档丰富、客服支持好，比较适合新手或者对定制化要求不高的投资者使用。另一种方式是使用API自行开发交易平台和策略。这种方法技术门槛相对较高，需要由有一定编程能力的人来完成。
交易平台简介
在前面的回测章节中已经简单介绍过一些第三方平台。比如Multicharts、TradeBlazer、文华财经、金字塔等。还有一些刚兴起的，基于Web和Python的类QuantOpian平台，比如优矿、聚宽等。当然有的券商或者期货公司也会有自己开发的平台。这些平台不仅支持回测功能，同时还支持实盘交易功能。
不同平台对交易接口的支持是不一样的，而且还会不断发生变化。因为接口和平台众多，它们特点也各不相同，所以找到一个合适的自动交易平台是很不容易的，是需要花费大量时间去研究和测试的。
交易框架 vn.py
除了使用第三方平台之外，我们还可以使用API自行开发。现有的API中，底层大多是基于C++、C＃等语言开发的，开发起来比较烦琐。
这个框架将市面上大量的接口包装成了统一的Python语言接口。所以基于vn.py开发的效率要高很多。截至目前，vn.py已经包含了如下接口：
□CTP (ctp)
□飞马（femas)
□LTS (Its)
□中信证券期权（cshshlp)
□金仕达黄金（ksgold)
□金仕达期权（ksotp)
□飞鼠（sgit)
□飞创（xspeed)
□QDP (qdp)
□上海直达期货（shzd)
□Interactive Brokers(ib)
□OANDA (oanda)
□OKCOIN (okcoin)
□火币（huobi)
□链行（Ihang)
可以看到，支持期货的接口占了大多数，支持证券（股票）的接口很少。这与国内的市场环境是有关系的。期货的交易接口开放程度更高，也更成熟，股票的交易接口相对来说并没有那么成熟。
需要注意的是，并不是所有的交易接口都对大众开放。很多接口会有一些政策方面的规定。具体情况需要咨询相应的经纪商。由于vn.py一直在不断更新，因此这里作为参考。
 vn.py的安装和配置
vn.py的安装方法可能会随着版本的更新而有所不同。具体请参考官方网站。这里用于安装说明的是vn.py 2.0.6版本，为参考。

安装 VN Studio
运行vn.py，第一步需要准备Python 环境。再也不用像1.0时代那样需要折腾半天安装Anaconda、三方模块、MongoDB数据库等等，vn.py 2.0只有一个步骤，安装由vn.py 核心团队针对量化交易开发的 Python 发行版——VN Studio 即可。

打开官网VeighNa量化社区 - 你的开源社区量化交易平台 (vnpy.com)，正中央左边的金色按钮就是最新版本VN Studio的下载链接（3.8版本），认准金色按钮就行。

下载完成后双击运行，会看到一个很常见的软件安装界面，安装目录推荐选择默认的C:\vnstudio，后续我们都会以该目录作为VN Studio的安装路径，当然也可以根据自己的需求将其安装到其他目录，然后一路点击"下一步"按钮完成傻瓜式安装即可。

运行VN Station
安装完成后，回到桌面上就能看到VN Station的快捷方式了。双击启动后，将会看到VN Station的登录框，。对于首次使用的用户，请点击微信登录后，扫描二维码注册账号，请牢记用户名和密码（同样该用名和密码也可用于登录社区论坛VeighNa量化社区 - 你的开源社区量化交易平台 (vnpy.com))，后续使用可以直接输入用户名和密码登录，勾上"保存"勾选框自动登录更加方便。
登录后看到的就是VN Station主界面了，上方区域显示的是目前社区，论坛最新的置顶精华主题（目前注册人数刚破44353人，我注册在44353位，每日精华做不到，每周两三篇还是有的），下方的五个按钮则是VN Station提供的量化相关功能按钮，具体说明如下。

□社区：一键启动vn.py社区。
□交易：支持灵活配置加载交易接口和策略模块的专业版VN Trader（主要在这里）。

□投研：启动Jupyter Notebook交互式研究环境。
□加密：打开浏览器访问社区论坛的"提问求助"板块，如果遇到问题就在此处快速提问。
□更新：傻瓜式更新vn.py和VN Station，没有更新时按钮是点不了的，只在有更新时按钮才会亮起。

启动交易
由于VN Trader Lite是一键式启动，无须配置，因此这里就只讲解交易模块。
点击按钮后弹出的第一个对话框，是选择VN Trader运行时目录，这里默认是当前操作系统的用户目录（User Path)，比如我的的路径就是C:\Users\59980。

vn:py 2.0对Python 源代码和运行时文件进行了分离，VN Trader运行过程中产生的所有配置文件、临时文件、数据文件（使用SQLite数据库），都会放置在运行时目录下的vntrader文件夹中。
VN Trader启动时，会检查当前目录是否存在．vntrader文件夹，若有就直接使用当前目录作为运行时目录，若找不到则会使用默认的用户目录（并在其中创建．vntrader 文件夹）。
大多数情况下，使用操作系统默认的用户目录就是最便捷的方案，在上述窗口中直接点击右下角的"选择文件夹"按钮，开始配置VN Trader，如图所示：

在左侧选择所需要的底层交易接口，"介绍"一栏中我们可以看到每个接口所支持的交易品种。注意，部分接口存在冲突不能同时使用，下方的说明信息中会有详细介绍。
在右侧选择需要的上层应用模块，同样，在"介绍"一栏中可以看到该模块所提供的具体功能。各个上层应用之间并不存在冲突的情况，所以新手不妨全部加载了一个个地查看，后续在确定自己的交易策略后再按需加载。
点击"启动"按钮后，稍等几秒就会看到如下图所示的VN Trader主界面，下面就可以连接登录交易接口，开始执行交易了！

 CTA策略模块分析
下面就来看一下CTA策略模块里面的具体代码。
CtaTemplate是最基础的模板，CTA 策略全部继承了CtaTemplate，其中公开提供给用户使用的函数包含以下几种。
(1）构造函数
□_init＿函数：参数包括引擎对象（回测or实盘）和参数配置字典。
(2）回调函数
□on_init：策略初始化时被调用，通常是在这里加载历史数据回放（调用 on_tick或者onBar）来初始化策略状态。
□ on_start：策略启动时被调用。
□ on_stop：策略停止时被调用，通常会撤销掉全部活动委托。

□ on_tick：收到Tick推送时调用，对于非Tick级策略，会在这里合成K线后调用onBar。
□ on_bar：回测收到新的K线时调用，实盘由on_tick调用，通常是在这里编写策略主逻辑。□on_order：收到委托回报时调用，用户可以缓存委托状态数据以便于后续使用。
□on_stop_order：收到本地停止单状态变化时调用。
□ on_trade：收到成交时调用。
(3）交易函数
□buy：买入开仓，返回委托号vtOrderID。
□ sell：卖出平仓。
□ short：卖出开仓。
□ cover：买入平仓。
□ cancel_order：撤销委托，传入的参数是需要撤销的委托号vtOrderID。
现在我们基于示例策略strategyDualThrust.py来分析对应函数的使用方法。

注意datefeed是所连接的获取数据接口，如tushare:相关参考文档：GitHub - vnpy/vnpy_tushare: VeighNa框架的Tushare数据服务接口

这里需要先弄清楚阅读使用文档。

第一个入门策略
创建策略文件
首先要接触的一个概念是用户目录，即任何操作系统默认用来存放当前登录的用户运行程序时缓存文件的目录，假设登录的用户名为client，那么目录的路径分别如下。
口Windows下：C:\Users\client\。
□ Linux或Mac下：/home/client/。
上述即为最常用的用户目录路径，注意这只是常用情况，如果你的系统进行了特殊的配置修改，则路径可能会有所不同。
VN Trader默认的运行时目录即为操作系统用户目录，启动后会在用户目录下创建．vntrader 文件夹，用于保存配置和临时文件（有时可能会遇到奇怪的Bug，删除该文件夹后重启就能解决）。
同时CTA策略模块（CtaStrategyApp）在启动后，也会扫描位于VN Trader 运行时目录下的strategies文件夹来加载用户自定义的策略文件，以Windows为例，Strategies的路径为：C:\Users\client\strategies。注意，strategies文件夹默认是不存在的，需要用户自行创建。
进入strategies目录后，新建我们的第一个策略文件demo_strategy.py，然后用VS Code打开

定义策略类
新建的策略文件打开之后，内部空空如也，此时我们开始向其中添加代码，遵循一般传统，用MA策略作为演示，代码如下：

from vnpy.app.cta_strategy import(CtaTemplate,StopOrder,TickData,BarData,TradeData,OrderData,BarGenerator,ArrayManager)
class DemoStrategy(CtaTemplate):
    # 定义参数
    fast_window = 10
    slow_window = 20
    # 定义变量
    fast_ma0 = 0.0
    fast_ma1 = 0.0
    slow_ma0 = 0.0
    slow_ma1 = 0.0
    # 添加参数和变量名到对应的列表
    parameters=['fast_window','slow_window']
    variables=['fast_ma0', 'fast_ma1', 'slow_ma0', 'slow_ma1']
 
    def __init__(self, cta_engine, strategy_name, vt_symbol, setting):
 
        super().__init__(cta_engine, strategy_name, vt_symbol, setting)
        # K线合成器：用于从Tick合成分钟K线
        self.bg = BarGenerator(self.on_bar)
        # 时间序列容器：用于计算技术指标
        self.am= ArrayManager ()
    
    def on_init(self):
        """当策略被初始化时调用该函数"""
        # 输出日志，下同
        self.write_log("策略初始化")
        # 加载10天的历史数据用于初始化回放
        self.load_bar(10)
 
    def on_start(self):
 
        """当策略被启动时调用该函数"""
        self.write_log("策略启动")
        # 通知图形界面更新（策略的最新状态）
        # 若不调用该函数则界面不会发生变化
        self.put_event ()
 
    def on_stop(self):
        """当策略被停止时调用该函数"""
        self.write_log("策略停止")
        self.put_event ()
 
    def on_tick(self, tick: TickData):
        """通过该函数收到Tick推送"""
        self.bg.update_tick(tick)
 
    def on_bar(self, bar:BarData):
        """通过该函数收到新的1分钟K线推送"""
        am=self.am
        # 更新K线到时间序列容器中
        am.update_bar(bar)
        # 若缓存的K线数量尚不够计算技术指标，则直接返回
        if not am.inited:
            return
        
        # 计算快速均线
        fast_ma = am.sma(self.fast_window, array = True)
        self.fast_ma0 = fast_ma[-1] # T时刻数值
        self.fast_ma1 = fast_ma[-2] # T-1时刻数值
 
        # 计算慢速均线
        slow_ma = am.sma(self.slow_window, array = True)
        self.slow_ma0 = slow_ma[-1]
        self.slow_ma1 = slow_ma[-2]
        
        # 判断是否金叉
        cross_over= (self.fast_ma0 > self.slow_ma0 and self.fast_ma1 < self.slow_ma1)
        # 判断是否死叉
        cross_below=(self.fast_ma0 < self.slow_ma0 and self.fast_ma1 > self.slow_ma1)
        
        # 如果发生了金叉
        if cross_over:
            # 那么为了保证成交，在K线收盘价上加5发出限价单
            price = bar.close_price + 5
            # 若当前无仓位，则直接开多
            if self.pos == 0:
                self.buy(price, 1)
            # 若当前持有空头仓位，则先平空，再开多
            elif self.pos < 0:
                self.cover(price,1)
                self.buy(price, 1)
 
        # 如果发生了死又
        elif cross_below:
            price= bar.close_price - 5
            # 若当前无仓位，则直接开空
            if self.pos == 0:
                self.short(price, 1)
                # 若当前持有空头仓位，则先平多，再开空
            elif self.pos> 0:
                self.sell(price, 1)
                self.short(price, 1)
        self.put_event ()
 
    """通过该函数收到委托状态更新推送"""
    def on_order(self,order: OrderData):
        pass
 
    """通过该函数收到成交推送"""
    def on_trade(self, trade: TradeData): # 成交后若策略逻辑仓位发生变化，则需要通知界面更新
        self.put_event ()
 
    """通过该函数收到本地停止单推送"""
    def on_stop_order(self, stop_order: StopOrder):
        pass

 在文件头部的一系列import中，最重要的就是CtaTemplate，这是我们开发CTA策略所用的策略模板基类，策略模板提供了一系列以on＿开头的回调函数，用于接收事件推送，以及其他主动函数用于执行操作（委托、撤单、记录日志等）。
所有开发的策略类，都必须继承CtaTemplate基类，然后在需要的回调函数中实现策略逻辑，即当某件事情发生时，我们需要执行的对应操作：比如，当收到1分钟K线推送时，我们需要计算均线指标，然后判断是否要执行交易。

设置参数变量

所有的量化交易策略必然都会涉及参数和变量这两个与数值有关的概念。
参数是策略内部的逻辑算法中用来控制结果输出的一些数值，在策略类中需要定义出这些参数的默认数值，代码如下：

# 定义参数
fast_window=10
slow_window=20

定义完后，还需要将参数的名称（字符串）添加到parameters列表中，代码如下：

parameters=['fast_window','slow_window']

这一步操作是为了让系统内的策略引擎，得以知道该策略包含哪些参数，并在初始化策略时弹出相应的对话框让用户填写，或者在命令行模式下直接将配置字典中对应的key 的value 赋值到策略变量上。
变量则是策略内部的逻辑算法在执行过程中用来缓存中间状态的一些数值，在策略类中同样需要定义出这些变量的默认数值，代码如下：

# 定义变量
fast_ma0 = 0.0
fast_ma1 = 0.0
slow_ma0 = 0.0
slow_ma1 = 0.0

定义完之后，还需要将变量的名称（字符串）添加到variables列表中，代码如下：

variables=['fast_ma0', 'fast_ma1', 'slow_ma0', 'slow_ma1']

与参数类似，这一步操作是为了让系统内的策略引擎，得以知道该策略包含哪些变量，并在GUI（图形界面）上更新策略状态时将这些变量的最新数值显示出来，同时在将策略运行状态保存到缓存文件中时将这些变量写进去（实盘中每天关闭策略时会自动缓存）。
需要注意的事项具体如下。
□ 无论是变量还是参数，都必须定义在策略类中，而非策略类的__init__函数中。

□ 参数和变量，均只支持Python中的四种基础数据类型，即str、int、float、bool,若使用其他类型则会导致各种出错（尤其需要注意的是不要用list、dict等容器）;

□如果在策略逻辑中，确实需要使用list、dict之类的容器来进行数据缓存，那么请在__init__函数中创建这些容器。

交易逻辑实现

前文已经提到过，在vn.py的CTA 策略模块中，所有的策略逻辑都是由事件来驱动的。下面列举一些事件进行说明。
□ 策略在执行初始化操作时，会收到on_init函数的调用，此时可以加载历史数据，来进行技术指标的初始化运算。
□ 一根新的1分钟K线走完时，会收到on_bar函数的调用，参数为这根K线对象的BarData.
□ 策略发出的委托，状态发生变化时，会收到on_order函数的调用，参数为该委托的最新状态OrderData。
对于最简单的双均线策略的DemoStrategy来说，我们不用关注委托状态变化和成交推送之类的细节，只需要在收到K线推送时（on_bar函数中）执行交易相关的逻辑判断即可。
每次一根新的K线走完时，策略会通过on_bar函数收到这根K线的数据推送。注意，此时收到的数据只有该K线，但大部分技术指标在计算时都会需要过去N个周期的历史数据。
所以为了计算均线技术指标，我们需要使用一个称为时间序列容器 ArrayManager的对象，用于实现K线历史的缓存和技术指标的计算，在策略的__init__函数中创建该对象，代码如下：

# 时间序列容器：用于计算技术指标
self.am= ArrayManager ()

在on_bar函数的逻辑中，第一步需要将K线对象推送到该时间序列容器中，代码如下：

am=self.am
# 更新K线到时间序列容器中
am.update_bar(bar)
# 若缓存的K线数量尚不够计算技术指标，则直接返回
if not am.inited:
    return

为了满足技术指标计算的需求，我们通常最少需要N根K线的缓存（N默认为100),在推送进ArrayManager对象的数据不足N之前，是无法计算出所需要的技术指标的，对于缓存的数据是否已经足够的判断，通过am.inited变量可以很方便地进行判断，在inited 变为True之前，都应该只是缓存数据而不进行任何其他操作。
当缓存的数据量满足需求之后，我们可以很方便地通过am.sma函数来计算均线指标的数值，代码如下：

        # 计算快速均线
        fast_ma = am.sma(self.fast_window, array = True)
        self.fast_ma0 = fast_ma[-1] # T时刻数值
        self.fast_ma1 = fast_ma[-2] # T-1时刻数值
 
        # 计算慢速均线
        slow_ma = am.sma(self.slow_window, array = True)
        self.slow_ma0 = slow_ma[-1]
        self.slow_ma1 = slow_ma[-2]

 注意，这里我们传入了可选参数array=True，因此返回的fast_ma为最新移动平均线的数组，其中最新一个周期（T时刻）的移动均线ma数值可以通过-1下标来获取，上一个周期（T-1时刻）的ma数值可以通过-2下标来获取。
快慢两根均线在T时刻和T-1时刻的数值之后，我们就可以进行双均线策略的核心逻辑判断了，即判断是否发生了均线金叉或者死叉，代码如下：

        # 判断是否金叉
        cross_over= (self.fast_ma0 > self.slow_ma0 and self.fast_ma1 < self.slow_ma1)
        # 判断是否死叉
        cross_below=(self.fast_ma0 < self.slow_ma0 and self.fast_ma1 > self.slow_ma1)

所谓的均线金叉，是指T-1时刻的快速均线fast_ma1低于慢速均线slow_ma1，而T时刻时快速均线fast_ma0大于或等于慢速均线slow_ma0，实现了上穿的行为（即金叉）。均线死叉则是相反的情形。
若发生了金叉或者死叉，则需要执行相应的交易操作，代码如下：

        # 如果发生了金叉
        if cross_over:
            # 那么为了保证成交，在K线收盘价上加5发出限价单
            price = bar.close_price + 5
            # 若当前无仓位，则直接开多
            if self.pos == 0:
                self.buy(price, 1)
            # 若当前持有空头仓位，则先平空，再开多
            elif self.pos < 0:
                self.cover(price,1)
                self.buy(price, 1)
 
        # 如果发生了死又
        elif cross_below:
            price= bar.close_price - 5
            # 若当前无仓位，则直接开空
            if self.pos == 0:
                self.short(price, 1)
                # 若当前持有空头仓位，则先平多，再开空
            elif self.pos> 0:
                self.sell(price, 1)
                self.short(price, 1)
        self.put_event ()

对于简单双均线策略来说，若处于持仓的状态中，则金叉后拿多仓，死叉后拿空仓。
所以当金叉发生时，我们需要检查当前持仓的情况。如果没有持仓（self.pos==0)，说明此时策略刚开始进行交易，则应该直接执行多头开仓操作（buy)。如果此时已经持有空头仓位（self.pos <0)，则应该先执行空头平仓操作（cover)，然后同时立即执行多头开仓操作（buy)。为了保证成交（简化策略），我们在下单时选择加价的方式来实现（多头＋5，空头﹣5)。
注意，尽管这里我们选择使用双均线策略来做演示，但在实践经验中，简单均线类的策略效果往往非常差，千万不要拿来进行实盘操作，也不建议在此基础上进行扩展开发。

实盘K线合成

DemoStrategy的双均线交易逻辑，可以通过超价买卖的方式来保证成交，从而忽略撤单、委托更新、成交推送之类更加细节的事件驱动逻辑。
但在进行实盘交易时，任何交易系统（不管是期货CTP、还是数字货币BITMEX等）都只会推送最新的Tick更新数据，而不会有完整的K线推送，因此用户需要自行在本地完成Tick到K线的合成逻辑。
vn.py也提供了完善的K线合成工具BarGenerator，用户只需在策略的__init__函数中创建实例即可，代码如下：

        # K线合成器：用于从Tick合成分钟K线
        self.bg = BarGenerator(self.on_bar)

其中，BarGenerator对象创建时，传入的参数（self.on_bar）是指当1分钟K线走完时所触发的回调函数。
在实盘策略收到最新的Tick 推送时，我们只需要将TickData更新到BarGenerator中即可，代码如下：

    def on_tick(self, tick: TickData):
        """通过该函数收到Tick推送"""
        self.bg.update_tick(tick)

 当BarGenerator发现某根K线走完时，会将过去1分钟内的Tick数据合成的1分钟K 线推送给策略，自动调用策略的on_bar函数，执行上面讲解的交易逻辑。

on_tick逻辑

on_tick属于回调函数。所谓回调函数，大致可以理解为不是用户主动调用的函数，而是由对应的服务端调用的函数。在这里，on_tick函数就是每当产生一个新的行情数据的时候，就会调用该函数，函数的参数就是对应的tick信息。
strategyDualThrust.py主要是完成了计算K线的工作。然后，在产生一个新的K线的时候，调用on_bar，具体的策略逻辑是写在 on_bar 里面的。也就是说，策略的计算信号的频率是以K线为单位的。
主要代码如下：

if tickMinute != self.barMinute:
    if self.bar:
        self.on_bar(self.bar)
 
    bar = VtBarData()
    bar.vtSymbol = tick.vtSymbol
    bar.symbol = tick.symbol
    bar.exchange = tick.exchange
 
    bar.open = tick.lastPrice
    bar.high = tick.lastPrice
    bar.low = tick.lastPrice
    bar.close = tick.lastPrice
 
    bar.date = tick.date
    bar.time = tick.time
    bar.datetime = tick.datetime # K线的时间设为第一个Tick 的时间
    
    self.bar=bar                 # 这种写法可以减少一层访问，从而加快速度
    self.barMinute=tickMinute    # 更新当前的分钟
else:                            # 否则继续累加新的K线
    bar= self.bar                # 这种写法同样是为了加快速度
    bar.high= max(bar.high, tick.lastPrice)
    bar.low= min(bar.low, tick.lastPrice)
    bar.close = tick.lastPrice

可以看到，判断是否产生新的K线的依据是判断当前tick的分钟是不是与对应bar的分钟相等。如果不相等，则说明产生了新的K线，于是就要调用On_bar 函数计算策略逻辑。同时，也新增一个Bar对象，然后初始化相应信息，作为下一根Bar。如果没有产生新的Bar，那么只需要更新当前Bar的high、low、close数据即可，也不需要调用On_bar 函数。

on_bar逻辑

首先，我们需要维护一个报单列表orderList，调用on_bar的时候，最开始应撤销之前未成交的所有委托。这一步很重要，否则报单的管理就可能会变得非常混乱，甚至导致出错。

# 撤销之前发出的尚未成交的委托（包括限价单和停止单）
for orderID in self.orderList:
    self.cancelOrder (orderID)
self.orderList = []

之后就是计算相应的指标值，根据指标值判断是否产生交易信号，代码如下：

# 撤销之前发出的尚未成交的委托（包括限价单和停止单）
for orderID in self.orderList:
    self.cancelOrder (orderID)
self.orderList = []
 
if lastBar.datetime.date() != bar.datetime.date():
    # 如果已经初始化
    if self.dayHigh:
        self.range = self.dayHigh - self.dayLow
        self.longEntry = bar.open + self.k1 * self.range
        self.shortEntry = bar.open - self.k2 * self.range
 
    self.dayOpen = bar.open
    self.dayHigh = bar.high
    self.dayLow = bar.low
 
    self.longEntered = False
    self.shortEntered = False
else:
    self.dayHigh=max(self.dayHigh, bar.high)
    self.dayLow= min(self.dayLow, bar.low)

再之后就是根据信号进行的交易逻辑了。这里需要注意的是，pos变量是由引擎维护的。但是经过测试，必须要在 on_trade(）函数里加上 self.put_event(）才能保证 pos更新的及时和准确性。具体代码如下：

if bar.datetime.time() < self.exitTime:
    # 没有仓位
    if self.pos == 0:
        if bar.close> self.dayOpen:
            if not self.longEntered:
                vtOrderID = self.buy(self.longEntry, self.fixedSize, stop = True)
                self.orderList.append(vtOrderID)
        else:
            if not self.shortEntered:
                vtOrderID = self.short (self.shortEntry, self.fixedSize, stop = True)
                self.orderList.append(vtOrderID)
 
    # 持有多头仓位
    elif self.pos > 0:
        self.longEntere = True
        # 多头止损单
        VtOrderID = self.sell(self.shortEntry, self.fixedSize, stop = True)
        self.orderList.append(vtOrderID)
        # 空头开仓单
        if not self.shortEntered:
            vtOrderID = self.short(self.shortEntry, self.fixedSize, stop=True)
            self.orderList.append(vtOrderID)
 
    # 持有空头仓位
    elif self.pos < 0:
        self.shortEntered=True
        # 空头止损单
        vtOrderID = self.cover(self.longEntry, self.fixedSize, stop=True)
        self.orderList.append(vtOrderID)
    # 多头开仓单
        if not self.longEntered:
            vtOrderID = self.buy (self.longEntry, self.fixedSize, stop=True)
            self.orderList.append (vtOrderID)
 
    # 收盘平仓
    else:
        if self.pos > 0:
            vtOrderID = self.sell(bar.close * 0.99, abs(self.pos))
            self.orderList.append (vtOrderID)
        elif self.pos < 0:
            vtOrderID = self.cover (bar.close * 1.01, abs(self.pos))
            self.orderList.append(vtOrderID)

从上述这段代码中，可以看到，逻辑主要分为了三大块，分别对应着无仓位、有多头仓位、有空头仓位的情况。这种按三种不同仓位分块的写法是CTA策略中最常见的写法。另外，可以看到，每次下单的时候，都会将返回的订单编号添加到维护的订单列表中。
讲到这里，主要的策略逻辑已经介绍完毕。需要注意的是，这只是一个样例策略，并不是能够实盘的策略。因为有很多其他的细节和问题还没有考虑到，比如，如果下单没有成交应该怎么处理？断网后应该怎么处理？等等。如果需要进行实盘交易，那么很多细节问题都是要自行处理的。

策略的两种模式

一般来说，编写策略可分为两种模式。

一种是策略逻辑，只负责计算信号，并在信号出现的时候通知系统开平仓。具体的下单算法、回报处理等，策略逻辑里面不处理，而是交由底层系统模块来处理，策略编写人员不用考虑。这种方式相对来说比较简单，比较适合频率较低的策略，比如30分钟、小时、日线数据。
另一种模式是策略里面本身需要实现下单算法、回报处理等更细粒度的逻辑。这种模式来说相对比较复杂，因为报单的处理是难度较高的一块。这种模式比较适合于1分钟以下的高频交易。
对于第一种模式，vn.py提供了一个对应的模板，即ctaTemplate.py 里面的 TargetPosTemplate 类。基于TargetPosTemplate开发策略，无需再调用buy/sell/cover/short这些具体的委托指令，只需要在策略逻辑运行完成之后调用setTargetPos设置目标持仓，底层算法就会自动完成相关的交易，该模式比较适合不擅长管理交易挂撤单细节的用户。在TargetPosTemplate 里面，核心的代码就是仓位同步算法。此算法的实现在trade函数里面，具体代码如下：

def trade(self):
    """执行交易"""
    # 先撒销之前的委托
    for vtOrderID in self.orderList:
        self.cancelOrder(vtOrderID)
        self.orderList=[]
 
    # 如果目标仓位与实际仓位一致，则不进行任何操作
    posChange=self.targetPos - self.pos
    if not posChange:
        return
    
    # 确定委托基准价格，有tick数据时优先使用，否则使用bar
    longPrice = 0
    shortPrice = 0
    if self.lastTick:
        if posChange > 0:
            longPrice = self.lastTick.askPrice1 + self.tickAdd
        else:
            shortPrice = self.lastTick.bidPricel - self.tickAdd
    
    else:
        if posChange > 0:
            longPrice = self.lastBar.close + self.tickAdd
        else:
            shortPrice = self.lastBar.close - self.tickAdd
    
    # 回测模式下，采用合并平仓和反向开仓的委托方式
    if self.getEngineType() == ENGINETYPE_BACKTESTING:
        if posChange > 0:
            vtOrderID = self.buy(longPrice,abs(posChange))
        else:
            vtOrderID = self.short(shortPrice,abs(posChange)) 
        self.orderList.append (vtOrderID)
 
    # 实盘模式下，首先确保之前的委托都已经结束（全成、撤销)
    # 然后先发送早仓委托，等待成交之后，再发送新的开仓委托
    else:
        # 检查之前的委托是否都已结束
        if self.orderList:
            return
        # 买入
        if posChange > 0:
            if self.pos < 0:
                vtOrderID = self.cover(longPrice,abs(self.pos))
            else:
                vtOrderID = self.buy(longPrice,abs (posChange))
 
        # 卖出
        else:
            if self.pos > 0:
                vtOrderID = self.sell(shortPrice, abs(self.pos))
            else:
                vtOrderID = self.short(shortPrice, abs(posChange))
        self.orderList.append(vtOrderID)

第二种模式，基于CtaTemplate开发即可实现。因为 CtaTemplate 暴露了相应的函数给用户实现。其中，主要的函数是On_tick()、OnOrder()、OnTrade()、buy()、sell()、short()、cover().
On_tick(）是行情的回调函数，每出现一个行情数据，就会调用一次这个函数，所以里面的逻辑每个tick都会执行一次。
OnOrder(）是报单状态变化的函数，比如下单成功或者失败，撤单成功或者失败，都会收到相应的回报。
OnTrade(）是报单出现成交之后回调的函数。需要注意的是，报单不一定全部成交，所以有时候也会返回部分成交的信息。
下面就来列举一个例子，说明如何利用这些函数来完成相应的功能。在高频交易中，有时候为了抢时间，我们需要在报单成交之后，立刻发出止盈单。这个功能就可以在OnTrade(）里面实现了。以下是一个成交之后立刻发出止盈单的示例：

def onTrade(self, trade):
    self.putEvent ()
if trade.offset == u'开仓':
# 下止盈单
    if trade.direction == u'多':
        vtOrderID = self.sell(trade.price + self.profit_tick * self.tick_value, trade.volume)
        self.orderList.append (vtOrder ID)
else:
    vtOrderID = self.cover(trade.price - self.profit_tick * self.tick_value, trade.volume)
    self.orderList.append(vtOrderID)

在这段代码里面，我们首先判断收到的成交回报是不是开仓单，如果是开仓多单，那么就下相应成交数量的止盈平仓空单；如果是开仓空单，那么就下相应成交数量的止盈平仓多单。
这是一个比较简单的例子，下单算法可能会很复杂，需要根据实际情况具体确定。