236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

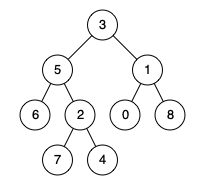
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中

class Solution {
public:
    TreeNode* dfs(TreeNode* root,TreeNode* p,TreeNode* q){
        if(root == p || root == q || !root) return root;
        //why后序。
        //因为要通过孩子情况一直向上反映
        TreeNode* left = dfs(root->left,p,q);//要么返回q，要么p，要么空
        TreeNode* right = dfs(root->right,p,q);
        if(right && left) return root;//左右孩子都不为空，那必然就是pq。
        else if(right && !left) return right; //右不为空。那就将右一直向上返回第二层，然后遍历右子树，必然就有
        else return left;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //只有两个情况。pq都在同一个树下。
        //或者就是p在q之下，q在p之下。
        return dfs(root,p,q);
    }
};