[python 刷题] 33 Search in Rotated Sorted Array

[python 刷题] 33 Search in Rotated Sorted Array

题目：

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

这道题也是一道 sorted array，和 [python 刷题] 153 Find Minimum in Rotated Sorted Array 的处理逻辑有点像，不过 [python 刷题] 153 Find Minimum in Rotated Sorted Array 只要找最小数，因此只要判断 nums[m] 和 nums[r] 的关系即可，这里的情况稍微复杂一些。

图像上显示，一共会有两种情况：

每个情况又会延伸出两个需要解决的对应情况，因此总共需要手动处理 4 种对应的情况

1. 找出比图 1 中高亮的元素小的元素

   这个处理起来比想象中的稍微麻烦一些，因为比 9 小的值可能同时存在于两个 cluster 间：

   

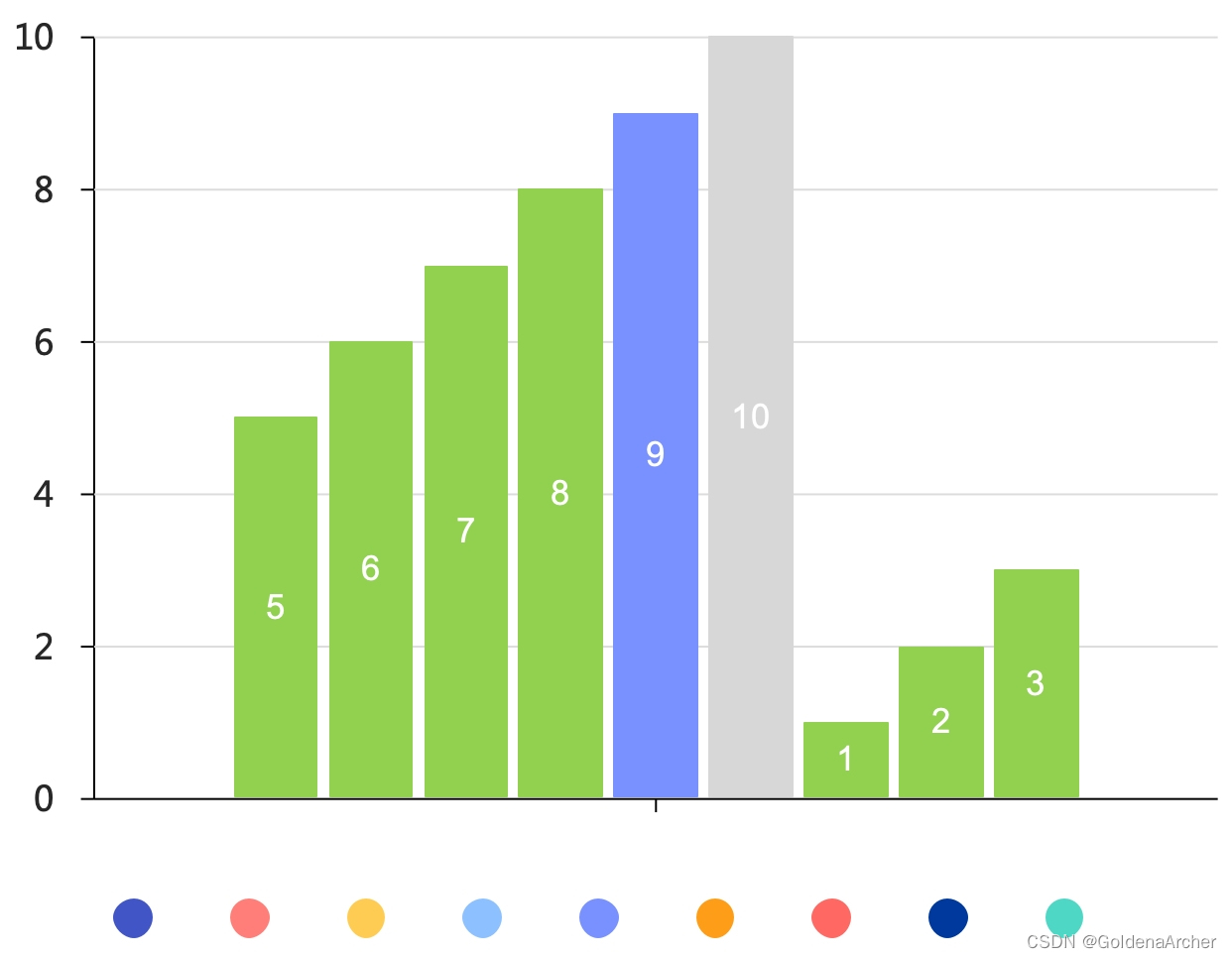
   因此这个时候还需要判断 target 是否比 nums[l] 小，如果比 nums[l] 小，那么就一定在右边的 cluster 中

2. 找出比图 1 中高亮的元素大的元素

   这个情况比较简单，只要从右边的 cluster 中搜索即可

3. 找出比图 2 中高亮的元素大的元素

   这个情况与情况 1 一样，也会同时坐落于两个区间：

   

   也因此需要判断 target 和 nums[l] 之间的关系，如果 target 比 nums[l] 小，那么 target 一定坐落于右侧的 cluster

   反之 target 一定坐落于左侧的 cluster 中

4. 找出比图 2 中高亮的元素小的元素

   这一定在 cluster 的左边

一旦思路理清了，那么代码写起来也很容易了：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = (l + r) // 2
            if nums[m] == target:
                return m

            if nums[m] < nums[l]:
                # the it means there are 2 assending order in the curr subarray
                if target < nums[m] or target > nums[r]:
                    r = m - 1
                else:
                    l = m + 1
            else:
                if target > nums[m] or target < nums[l]:
                    l = m + 1
                else:
                    r = m - 1

        return -1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

另，如果刚开始的判断不是做 nums[m] < nums[l] 的话，记得要用 $\ge$: if nums[m] >= nums[l]: