质数距离 - 如何在较合理的时间复杂度内求2e9范围内的质数

求l、r之间的质数，范围在2e9，但l、r的差值不大，在1e6范围内

先求出 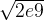内的质数，然后拿这个指数去筛[l, r]范围内的即可

#include
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;
 
const int N = 50010, M = 1000010;
 
int primes[N], cnt;
bool st[M];
int p[M];
 
void init()
{
	for(int i = 2; i < N; i ++)
	{
		if(!st[i])primes[cnt ++] = i;
		for(int j = 0; primes[j] * i < N; j ++)
		{
			st[primes[j] * i] = true;
			if(i % primes[j] == 0)break;
		}
	}
}
 
int main()
{
	IOS
	init();
	int cnt_tmp = cnt;
	
	ll l, r;
	while(cin >> l >> r)
	{
		if(l == 1)l = 2;
		
		memset(st, false, sizeof st);
		cnt = cnt_tmp;
		for(int i = 0; i < cnt; i ++)
		{
			ll start = max((ll)primes[i] * 2, (l + primes[i] - 1) / primes[i] * primes[i]);
			for(ll j = start; j <= r; j += primes[i])
			{
				st[j - l] = true;
			}
		}
		
		cnt = 0;
		for(int i = 0; i <= r - l; i ++)
		{
			if(!st[i])p[cnt ++] = i;
		}
		
		if(cnt < 2)
		{
			cout << "There are no adjacent primes." << endl;
			continue;
		}
		
		int min1 = 0, min2 = 2e9, max1 = 0, max2 = 0;
		for(int i = 0; i < cnt - 1; i ++)
		{
			if(p[i + 1] - p[i] < min2 - min1)
			{
				min1 = p[i];
				min2 = p[i + 1];
			}
			if(p[i + 1] - p[i] > max2 - max1)
			{
				max1 = p[i];
				max2 = p[i + 1];
			}
		}
		cout << min1+l << "," << min2+l << " are closest, " << max1+l << "," << max2+l << " are most distant." << endl;
	}
	
	return 0;
}

要注意的几个点：

1.对于每次筛最少要从primes[i] * 2开始，不能筛到质数 

2.在start计算过程中和j+的过程中很容易爆int，注意这部分开ll

3.求大于等于l的第一个p的倍数：(l + p - 1) / p * p