深度学习笔记之线性代数

深度学习笔记之线性代数

一、向量

在数学表示法中，向量通常记为粗体小写的符号（例如，x，y，z）当向量表示数据集中的样本时，它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风险，用一个向量表示一个患者，其分量为最近的生命特征、胆固醇水平、每天运动时间等。

可以使用下标来引用向量的任意元素

使用切片访问

向量只是一个数字数组，就像每个数组都有一个长度，向量的长度通常称为向量的维度（dimension）
可以通过调用Python的内置len()函数来访问张量的长度

当张量表示一个向量时，可以通过.shape属性访问向量的长度。对于只有一个轴的张量，形状只有一个元素。

二、矩阵

矩阵将向量从一阶推广到二阶。通常用粗体大写字母表示矩阵（例如X，Y，Z），在代码中表示具有两个轴的张量。

索引访问

求矩阵的转置

判断一个矩阵是否为对称矩阵。即这个矩阵是否等于它的转置矩阵。

三、张量算法的基本性质

两个形状相同的矩阵相加，会在这两个矩阵上执行元素加法

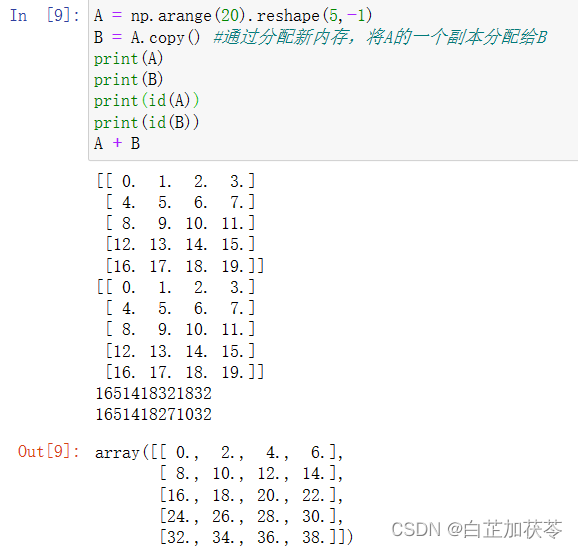
两个矩阵按元素乘法成为Hadamard积

将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都与标量相加或相乘

四、降维

计算向量中元素的和

为了通过求和所有行元素来降维，可以在调用函数时制定axis=0
也可以指定axis=1将通过汇总所有列的元素降维

沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和

计算任意形状张量的平均值

五、非降维求和

如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

六、点积

七、矩阵-向量积

八、矩阵-矩阵乘法

九、范数