基本的五大排序算法

江河入海，知识涌动，这是我参与江海计划的第6篇。

目录：

一，直接插入算法

二，希尔排序算法

三，选择排序

四，堆排序

五，冒泡排序算法

---

简介：

        排序算法目前是我们最常用的算法之一，据研究表明，目前排序占用计算机CPU的时间已高达百分之30到百分之50。可见，高效率的排序算法是我们必须掌握的基本算法之一，本篇博客就先跟大家介绍五种常用的排序算法：直接插入算法，希尔算法，选择算法，堆排序算法，冒泡算法。

一，直接插入算法

        直接插入算法的原理与我们打扑克牌时，进行不摸牌排序的效应一样。平常我们在打扑克牌时会不断的摸牌，每当我们摸到一个牌时就会往里面插入，使得我们手中的排有序。直接插入算法与之同理，其基本思想是把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列种，直到所有的记录插入完为止，得到一个新的有序序列，即摸牌效应，如下图，是插入排序的示意图：

---

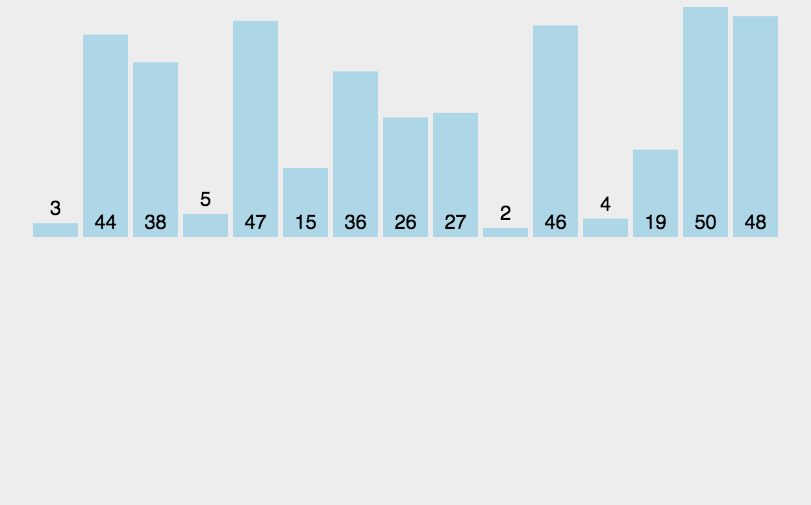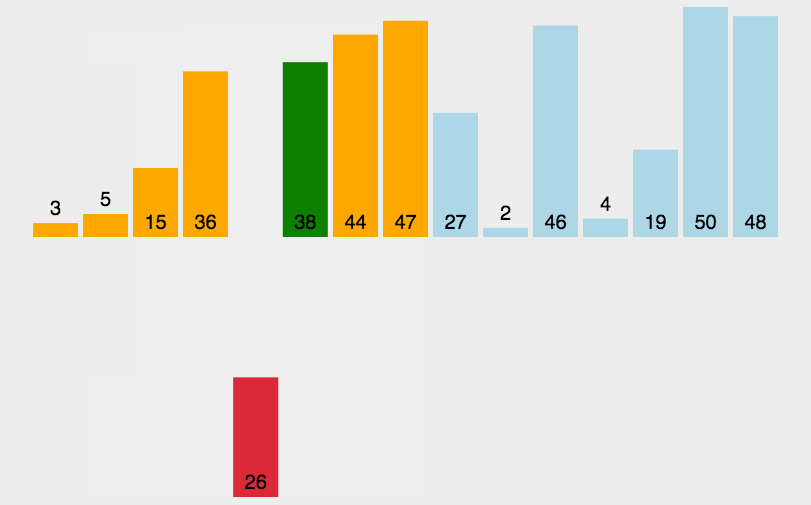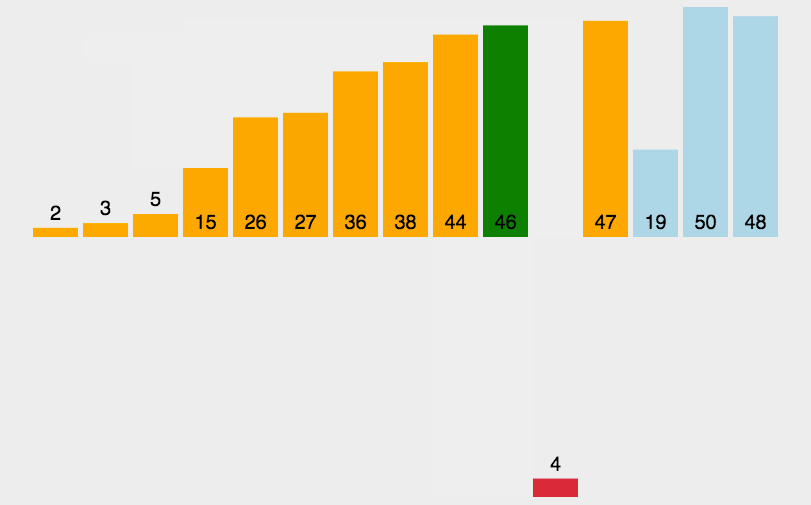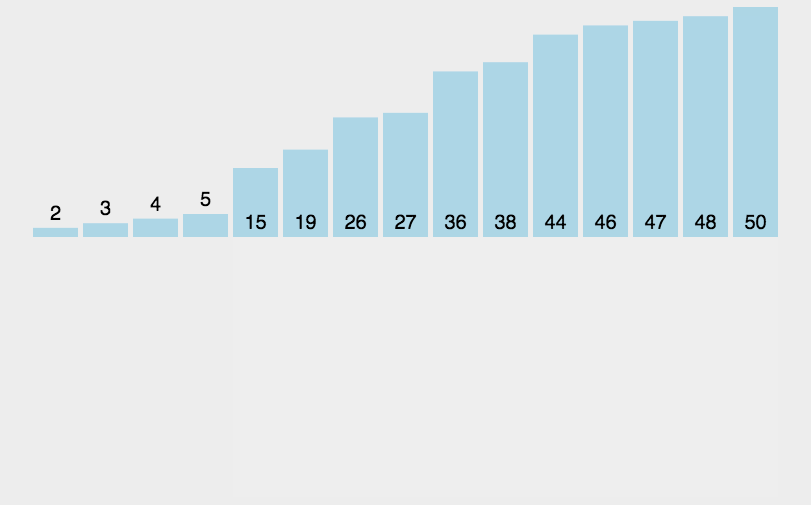
具体代码如下：

#include 
//直接插入算法
void InsertSort(int* a, int n) {
    for (int i = 0; i < n - 1; i++) {
 // [0,end]有序，把end+1位置的插入到前序序列,控制[0,end+1]有序
        int end = i;
        int next = a[i + 1];
 // 升序排列
        while (end >= 0) {
            if (a[end] > next) {
                a[end + 1] = a[end];
            }
            else {
                break;
            }
            end--;
        }
        a[end + 1] = next;
    }
}
int main() {
	int a[] = { 5,9,7,3,0,1,4,2,6,8 };
	InsertSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
		fprintf(stdout, "%d ", a[i]);
	}
	puts("");
	return 0;
}

运行图：

效率分析：

        不难发现，当为最好情况时（即有序排列），算法其实就是一次性遍历整个数组，时间复杂度为O(N)；当为最坏情况是(即要跟排列的顺序相反)，需要一直往首元素插入，此时的时间复杂度为O(N^2)，而空间复杂度始终为O(1)。                                                               

        我们之前接触过冒泡排序，其效率与之一样，但要注意的是，论时间复杂度它们虽是同一个档次，但细节上，如局部有序时，插入排序会更优，因为冒泡排序内部还需不断比较，这又要消耗时间。

---

二，希尔排序算法

        希尔排序是以插入排序为基础的排序。首先，该算法要设置一个分组，然后再用直接插入算法的思想进行预排序，预排序是将数据分组排序，每组数据之间有着一定的间距。如下图：

        上图中，第一组数据：9，5，8，5。第二组数据：1，7，6。第三组数据：2，4，3。三组数据先分别用直接插入算法进行预排序，排序后第一组数据为5，5，8，9。第二组数据为1，6，7。第三组数据为2，3，4。经过这些预排序后，整体的数据为5  1  2  5  6  3  8  7  4  9(不同颜色代表不同组中的数据，可直观的看出)。

        其中，将数据进行预排序的目的是大的数据更快的到后面去，小的数据更快的到前面去，其中，间距越大跳得越快，越不接近有序；间距越小跳得越慢，越接近有序，当间距为1时，直接为有序，因为，当间距为1时就是直接插入排序。

        希尔算法运用得原理就是给定一个间距值进行预排序，当间距值大于1时进行的排序为预排序，当间距值等于1时的排序就是直接插入排序，即排序已完成。本算法的效率很高，时间复杂度很难计算出，暂时先不研究这个，代码实现具体如下：

#include 
//希尔排序算法
void ShellSort(int* a, int n) {
	int grab = n;//开始时，设置间距grab = n;
	//当grab == 1时为直接插入算法，当grab > 1时为预排序
	while (grab != 1) {
		//grab /= 2;//不断的缩减grab的大小，直到grab == 1排序完成
		//由于grab一次性的缩减比较小，导致算法效率较低，以下的grab为改进算法，提高算法效率
		grab = grab / 3 + 1;//不断缩减间距grab的大小，直到grab == 1排序完成
		//以下是根据间距grab的大小来进行的插入排序,即预排序
		for (int j = 0; j < grab; j++) {
			for (int i = j; i < n - grab; i += grab) {
				int end = i;
				int x = a[i + grab];
				while (end >= 0) {
					if (a[end] > x) {
						a[end + grab] = a[end];
					}
					else {
						break;
					}
					end -= grab;
				}
				a[end + grab] = x;
			}
		}
	}
}
int main() {
	int a[] = { 5,9,7,3,0,1,4,2,6,8 };
	ShellSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
		fprintf(stdout, "%d ", a[i]);
	}
	puts("");
	return 0;
}

运行图：

---

三，选择排序

1，选择排序的基本思想：

        每一次从待排序的数据元素中选出最小或最大的一个元素，存放在系列的起始位置，即进行一趟选择，直到全部待排序的数据元素排完，如下图：

---

        以上就是选择排序的基本套路，但我们仔细思考下来，其实这种方法还有优化空间，当数据进行一趟选择时，我们可直接选出最大数和最小数，将其放在开头或末尾。然后再次进行遍历，直到头尾遍历相遇为止。代码如下：

#include 
//选择算法
void Swap(int* x1, int* x2) {
	int t = *x1;
	*x1 = *x2;
	*x2 = t;
}
void SelectSort(int* a, int n) {
	int begin = 0, end = n - 1;
	while (begin < end) {
		int max = begin, min = begin;
		//进行一趟遍历，确定最小值和最大值的下标,当前面遍历等于end时排序就已排好
		for (size_t i = begin + 1; i < end; i++) {
			if (a[max] < a[i]) {
				max = i;
			}
			if (a[min] > a[i]) {
				min = i;
			}
		}
		Swap(a + max, a + end);
		//当min在最后时，max与原先的end交换了位置，所以这时的end的下标已经变了
		if (min == end) {
			min = max;
		}
		Swap(a + min, a + begin);
		//前面排好，往后前进
		begin++;
		//后面排好，往前前进
		end--;
	}
}
int main() {
	int a[] = { 5,9,7,3,0,1,4,2,6,8 };
	SelectSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
		fprintf(stdout, "%d ", a[i]);
	}
	puts("");
	return 0;
}

运行图：

效率分析：

        不难发现，选择排序的时间复杂度和空间复杂度的最好情况和最坏情况都一样。时间复杂度：O(N^2)。空间复杂度：O(1)。

---

四，堆排序

        堆排序跟二叉堆排序一模一样，即先建立堆结构，然后进行堆的调整排序，使整体有序。要注意的是，升序排列首选大堆，降序排列首选小堆建立。由于这方面在之前讲解《树结构的讲解与二叉树的基本运用》时就已非常详细的说明，如有不懂的，可在本人那篇文章中学习一下，在这里我们就做简单介绍即可。其中要说明的是，堆排序在结构上是选择排序。以升序为例，结构图如下：

        由于原理与之前的二插堆一样，在这里就不做过多结构上的说明，下面是代码的实现和注释解说：

#include 
void Swap(int* x1, int* x2) {
	int t = *x1;
	*x1 = *x2;
	*x2 = t;
}
//向下调整算法
void Adjustdown(int* a, int n, int parent) {
	int child = 2 * parent + 1;
	while (child < n) {
		if (child + 1 < n && a[child] < a[child + 1]) {
			child++;
		}
		if (a[child] > a[parent]) {
			Swap(a + child, a + parent);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}
//以升序为例，升序用建大堆思想
void HeapSort(int* a, int n) {
	//从最后一层走起，因为要保证导入的parent往下都是有序的，即大堆建立
	for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
		Adjustdown(a, n, i);
	}
	//大堆建立后根为最大数，然后进行排序
	int end = n - 1;
	while (end > 0) {
		Swap(a, a + end);//因为根为最大数，要升序就要把最大数放入最后
		Adjustdown(a, end, 0);
		end--;
	}
}
int main() {
	int a[] = { 5,9,7,3,0,1,4,2,6,8 };
	HeapSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
		fprintf(stdout, "%d ", a[i]);
	}
	puts("");
	return 0;
}

运行图：

效率分析：

        堆排序可说分两大步骤：

        1，建堆，升序建大堆，降序建小堆，时间复杂度为：O(N*log*N)。空间复杂度：O(1)。

        2，排序，每排一个数据运用一次向下调整算法进行调整。时间复杂度为：O(N*log*N)。空间复杂度为：O(1)。

        因此，堆排序的时间复杂度为：O(N*log*N)。空间复杂度为：O(1)。

---

五，冒泡排序算法

        冒泡排序是一种交换排序，所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，此种交换的特点是将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

冒泡排序的原理图：

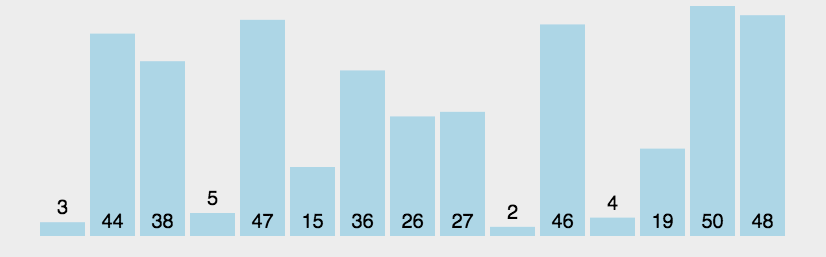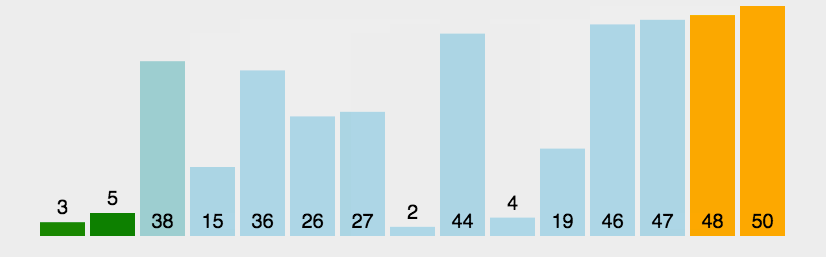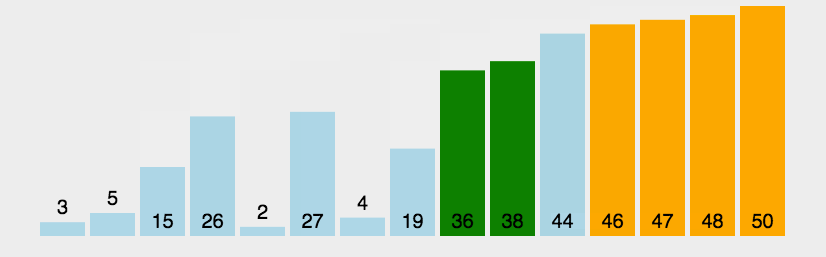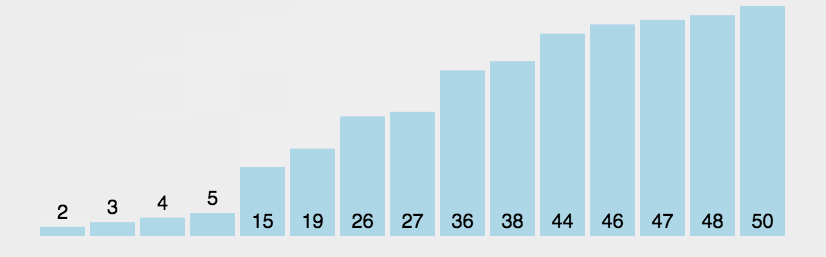
此种排序非常简单，具体代码如下：

#include 
void Swap(int* x1, int* x2) {
	int t = *x1;
	*x1 = *x2;
	*x2 = t;
}
//冒泡排序算法
void BubbleSort(int* a, int n)
{
	for (size_t j = 0; j < n; j++)
	{
		//用x进行控制，可提升算法的效率
		int x = 0;
		for (size_t i = 1; i < n - j; i++)
		{
			//进行排序，当没有进入此步时，说明是有序的
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				x = 1;
			}
		}
		//当x == 0时，说明序列是有序的，可直接跳出，提升算法的效率
		if (x == 0)
		{
			break;
		}
	}
}
int main() {
	//冒泡算法
	int a[] = { 5,9,7,3,0,1,4,2,6,8 };
	BubbleSort(a, sizeof(a) / sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); i++) {
		fprintf(stdout, "%d ", a[i]);
	}
	puts("");
	return 0;
}

运行图：

效率分析：

        首先我们来分析一下时间复杂度和空间复杂度，空间复杂度不难发现始终为：O(1)，时间复杂度要根据情况而定，当为最好情况时即有序，此时跟直接插入算法一样，相当于直接遍历了一遍，时间复杂度为：O(N)；当为最坏情况下时间复杂度为：O(N^2)。

        时间复杂度只是大约计算了一下，但要细刨里面的机构可知，冒泡排序每一趟都需要比较几次，这在系统中需要花费时间了完成，所以，冒泡排序其实效率很低，笔者不建议使用。

---

效率总分析：

        在五种排序算法中，效率最高的是希尔排序，效率最低的是冒泡排序，堆排序与希尔不相上下，但堆排序实现起来比较麻烦，因此个人建议首选希尔，直接插入算法比选择排序算法和冒泡略高一筹，但在进行大量数据排序时，效率都不高，因此，在五大基本排序中，希尔排序为最佳选择。