• 【C/C++笔试练习】二维数组、二维数组的访问，解引用，地址计算、计算糖果、进制转换

    文章目录

    C/C++笔试练习

    1.二维数组

    （1）二维数组的访问

      在int p[][4] = {{1}, {3, 2}, {4, 5, 6}, {0}};中，p[1][2]的值是（）

      A 1    B 0
      C 6    D 2
      

      在C++中，可以通过使用索引来访问二维数组中的元素。二维数组的索引是一个包含两个值的整数对，第一个值表示行，第二个值表示列。

      以下是访问二维数组元素的一般语法：

    arrayName[rowIndex][columnIndex]

    • 1

      其中，arrayName是二维数组的名称，rowIndex是行，columnIndex是列。索引值从0开始，因此第一行的索引是0，第一列的索引也是0。而且一般行的初始化都在 { } 中执行。

      例如，考虑以下二维数组的声明和初始化：

    int arr[3][4] = {{0, 1, 2, 3},
                 {4, 5, 6, 7},
                 {8, 9, 10, 11}};

    • 1
    • 2
    • 3

      要访问位于第二行第三列的元素，可以使用索引[1][2]，如下所示：

    int element = arr[1][2]; // element 的值为 6

    • 1

      注意，行索引和列索引都是从0开始的，所以arr[1][2]访问的是第二行第三列的元素，而不是第三行第四列的元素。

      

      所以对于上面的问题，二维数组是以行优先的方式在内存中连续存储的。对于一个声明为int p[][4]的二维数组，它表示的是一个具有未指定行数和4列的二维整型数组。

      在给定的初始化列表{{1}, {3, 2}, {4, 5, 6}, {0}}中，数组的第一行只有一个元素1，第二行有两个元素3和2，第三行有三个元素4、5和6，第四行有一个元素0。而且数组是按行优先的方式存储的。

      注意，对于一个部分初始化的二维数组，未被初始化的元素会被自动设置为0。 在给定的初始化列表{{1}, {3, 2}, {4, 5, 6}, {0}}中，第二行只初始化了两个元素3和2，所以第三个元素会被设置为0，所以元素在内存中的排列顺序是：

              1 0 0 0
              3 2 0 0
              4 5 6 0
              0 0 0 0

      对于索引p[1][2]，它表示的是第二行第三列的元素。在上面的内存布局中，第二行的元素是3 2 0 0，所以p[1][2]的值是0。

    在这里插入图片描述
       答案选：B

                 

    （2）二维数组的初始化

       以下能对二维数组a进行正确初始化的语句是（）

       A int ta[2][]={{0,1,2},{3,4,5}};         B int ta[][3]={{0,1,2},{3,4,5}};
       C int ta[2][4]={{0,1,2},{3,4},{5}};       D int ta[][3]={{0,2},{},{3,4,5}};

      
      在C++中，二维数组的初始化可以通过以下方式进行：

    // 声明一个3行4列的二维整型数组并初始化  
int arr[][4] = {{0, 1, 2, 3},
                 {4, 5, 6, 7},
                 {8, 9, 10, 11}};

    • 1
    • 2
    • 3
    • 4

      对二维数组进行初始化时，必须指定数组的行数和列数，或者省略行数但要指定列数。 每一对花括号内的数字都代表一行的所有元素。 请注意，第一对的花括号代表第一行，第二对的花括号代表第二行，以此类推。

      你也可以只对部分元素进行初始化，剩余的元素会被自动设置为0。例如：

    // 声明一个3行4列的二维整型数组并部分初始化  
int arr[3][4] = {{0, 1}, 
                 {4}, 
                 {8, 9, 10}}; 

    • 1
    • 2
    • 3
    • 4

      在这个例子中，第一行只有前两个元素被初始化，所以后两个元素会被设置为0。第二行只有一个元素被初始化，所以其它三个元素会被设置为0。第三行有三个元素被初始化，所以第四个元素会被设置为0。

      
      对于A:
    在这里插入图片描述
      
      对于B:
    在这里插入图片描述
      
      对于C:
    在这里插入图片描述
      
      对于D，因为VS来说，编译器为数组未初始化的行自动添加了0作为默认值， 但是这并不是C++标准的一部分，而是Visual Studio的特定行为。在其他编译器或平台上，这种省略子列表的初始化方式可能会导致编译错误或未定义的行为。因此，为了确保代码的可移植性和正确性，最好避免使用这种省略子列表的初始化方式，而是显式地指定每一行的元素。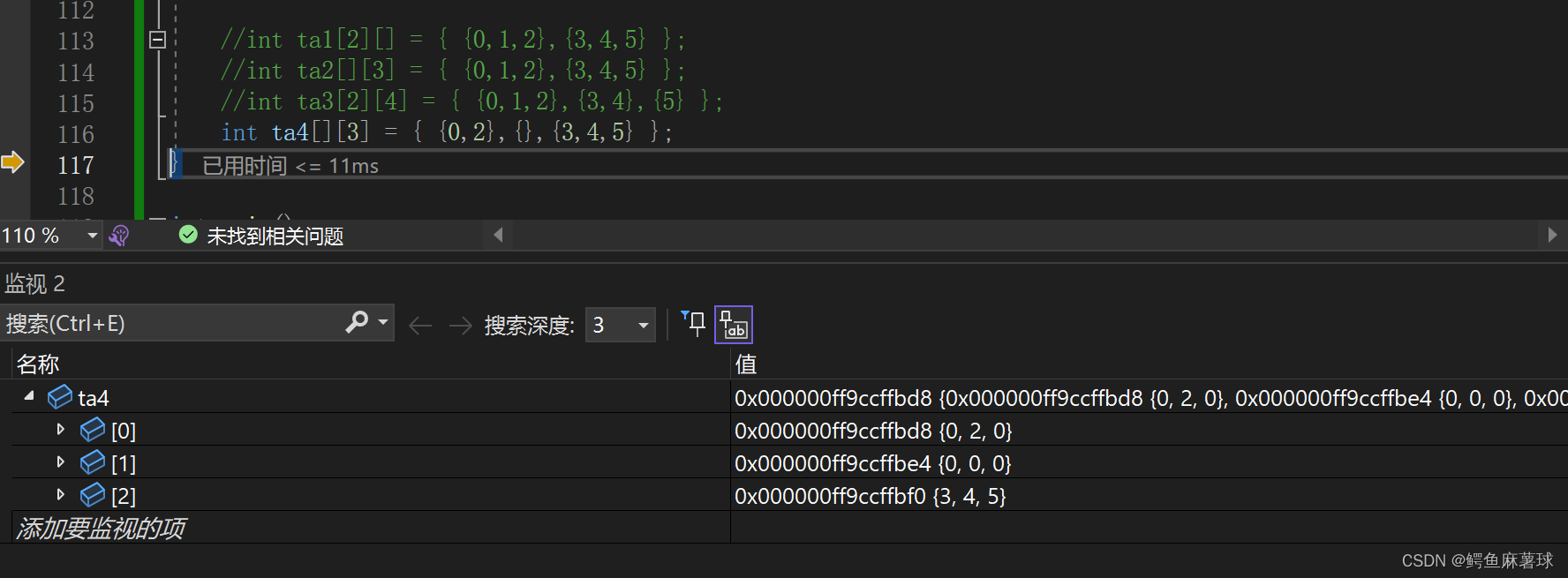

    在这里插入图片描述
       答案选：B

                 

    （3）二维数组的解引用

      数组a的定义语句为“float a[3][4];”，下列（）是对数组元素不正确的引用方法

      A a[i][j]       B *(a[i]+j)
      C * ( * (a+i)+j)    D * ( a+i * 4+j)
      

      在C++中，二维数组可以通过指针和解引用操作符来访问和修改其元素。下面是一些解引用二维数组的方法：

      使用数组索引操作符[]：

    int arr[3][4] = { {0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11} };  
int element = arr[i][j]; // 访问二维数组的元素

    • 1
    • 2

      使用指针和解引用操作符 * ：

    int arr[3][4] = { {0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11} };  
int (*p)[4] = arr; // p 是一个指向一行元素的指针  
int element = (*p)[j]; // 解引用指针 p，再访问元素

    • 1
    • 2
    • 3

      使用指针算术运算：

    int arr[3][4] = { {0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11} };  
int (*p)[4] = arr; // p 是一个指向一行元素的指针  
int element = p[i][j]; // 通过指针算术运算访问元素

    • 1
    • 2
    • 3

      需要注意的是，二维数组的名称本身就是一个指向首元素的指针，其类型为T (*)[N]，其中T是数组元素的类型，N是第二维的大小。因此，可以直接使用数组名称来访问和修改二维数组的元素。
      

      a是一个指向二维数组首元素的指针，其类型为float (* )[4]。在C++中，二维数组是按行优先的方式存储的，所以a+i会指向第i行的首元素，而 * (a+i)则会得到一个指向第i行首元素的指针，其类型为float*。因此，应该使用 * ( * ( a+i)+j)或者( * (a+i))[j]来访问数组元素，而不是 * ( a+i*4+j)。
    在这里插入图片描述

       答案选：D

                 

    （4）二维数组的解引用

       数组定义为”int a[4][5];”, 引用”*(a+1)+2″表示（）(从第0行开始)

      A a[1][0]+2      B a数组第1行第2列元素的地址
      C a[0][1]+2      D a数组第1行第2列元素的值

      对于一个定义为int a[4][5];的二维数组，a是一个指向二维数组首元素的指针，其类型为int (*)[5]。a+1会指向第二行的首元素，即a[1][0]的地址。

      因此，*(a+1)+2表示的是a[1][0]的地址加上2，也就是a[1][2]的地址。

      所以 *(a+1)+2 表示a数组第1行第2列元素的地址。

      选项A和C都是元素值的表达式+2，而不是地址表达式。

    在这里插入图片描述

       答案选：B

                 

    （5）多维数组的解引用

      下面哪个指针表达式可以用来引用数组元素a[i][j][k][l]（）

      A (((a+i)+j)+k)+l)      B * ( * ( * ( * (a+i)+j)+k)+l)
      C (((a+i)+j)+k+l)      D ((a+i)+j+k+l)

      根据上面的内容，对于一个二维数组，可以通过指针和解引用操作符来访问和修改其元素。对于数组元素a[i][j][k][l]，同样也可以使用如上操作来解引用数组：

      易得答案为B，在这个表达式中，a是一个指向多维数组首元素的指针，其类型为T (*)[N1][N2][N3][N4]，其中T是数组元素的类型，N1、N2、N3和N4是各维的大小。

      首先，a+i会指向第i个一维数组的首元素，即a[i][0][0][0]的地址。然后，(a+i)会得到一个指向第i个一维数组首元素的指针，其类型为T ( * )[N2][N3][N4]。接着，(a+i)+j会指向第i个一维数组的第j个二维数组的首元素，即a[i][j][0][0]的地址。依此类推，最终可以得到a[i][j][k][l]的地址，然后使用解引用操作符*来访问该元素的值。

      因此，选项B是正确的。选项A、C和D都表达了数组元素的地址，它们无法正确地引用多维数组的元素。

    在这里插入图片描述
       答案选：B

                 

    （6）二维数组的地址计算

      二维数组X按行顺序存储，其中每个元素占1个存储单元。若X[4][4]的存储地址为Oxf8b82140,X[9][9]的存储地址为Oxf8b8221c,则X[7][7]的存储地址为()。

      A Oxf8b821c4      B Oxf8b821a6
      C Oxf8b82198      D Oxf8b821c0
      

      二维数组X按行顺序存储，每个元素占1个存储单元。假设数组的第一个元素X[0][0]的存储地址为ADDR，每个元素占用的存储单元为SIZE，则X[i][j]的存储地址可以通过以下公式计算：

      ADDR(X[i][j]) = ADDR + (i * N + j) * SIZE

      其中，N是数组的第二维大小，即每行的元素个数。

      根据题目给出的信息，X[4][4]的存储地址为Oxf8b82140，X[9][9]的存储地址为Oxf8b8221c。由于每个元素占用1个存储单元，SIZE=1，因此可以计算出数组的第一个元素X[0][0]的存储地址。

      接下来，我们需要计算X[7][7]的存储地址。列出二元一次方程组。

      因此，X[7][7]的存储地址为Oxf8b821c4。

      注意：由于存储地址通常是以字节为单位的，而题目中给出的地址是以十六进制表示的，因此在计算时需要注意单位转换。在本题中，每个存储单元占用1个字节，因此可以直接用给定的十六进制地址进行计算。
    在这里插入图片描述
    在这里插入图片描述

       答案选：A

                 

    （7）二维数组和数组指针

      下面程序的输出结果是（）

    #include
void main()
{
	int n[][3] = {10,20,30,40,50,60};
	int (*p)[3];
	p=n;
	cout<<p[0][0]<<","<<*(p[0]+1)<<","<<(*p)[2]<<endl;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8

      A 10,30,50      B 10,20,30
      C 20,40,60      D 10,30,60

      首先，我们定义了一个二维数组n，其大小为未指定行数和3列。然后，我们定义了一个指向大小为3的整数数组的指针p，并将其指向n。

      接下来，我们输出p[0][0]，这等价于n[0][0]，即二维数组的第一行第一列的元素，其值为10。

      然后，我们输出*(p[0]+1)。p[0]是指向n[0]的指针，即指向第一行的指针。p[0]+1将指针向后移动一个元素，使其指向n[0][1]。解引用该指针得到n[0][1]的值，即20。

      最后，我们输出(*p)[2]。*p等价于n[0]，即第一行。(*p)[2]即第一行的第三个元素，其值为30。

    在这里插入图片描述

       答案选：B

                 

    2.编程题

    （8）计算糖果

    计算糖果

       解题思路：

       通过1、A - B = a   2、B - C = b  3、A + B = c  4、B + C = d 联立并且判断三元一次方程组是否有解及求解， 1+3可以得到A=(a+c)/2；4-2可以得到C=(d-b)/2；2+4可以得到B2=(b+d)/2，3-1可以得到B1=(c-a)/2；注意，如果B1不等B2则表达式无解。

    #include 
using namespace std;

int main() {
    int a,b,c,d;
    cin>>a>>b>>c>>d;
    int A=(a+c)/2;
    int C=(d-b)/2;
    int B1=(c-a)/2;
    int B2=(b+d)/2;
    if(B1!=B2)
    {
        cout<<"No"<<endl;
    }
    else
    {
        cout<<A<<" "<<B1<<" "<<C;
    }
    return 0;
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21

                 

    （9）进制转换

    进制转换

       解题思路：

     因为N进制数，每个进制位的值分别是X0N^ 0，X1N^ 1, X2*N^2…，X0，X1，X2就是这些进制位的值，就是就是进行取模余数就是当前低进制的位的值是多少，通过除掉进制数，进入下一个进制位的计算。

    #include 
#include
#include
using namespace std;

int main() {
    string s, table = "0123456789ABCDEF";
    int m, n;
    cin >> m >> n;
    bool flag = false;
    if(m==0) cout<<"0";
    
    //如果是负数，则转成正数，并标记一下
    if (m < 0) 
    {
        m = 0 - m;
        flag = true;
    }
    
    //按进制换算成对应的字符添加到s
    while (m) 
    {
        s += table[m % n];
        m /= n;
    }
    if (flag)
        s +='-';
    reverse(s.begin(), s.end());
    cout << s << endl;
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
  • 相关阅读:
    链式前向星核心代码解析 ← 数组模拟邻接表
    「PAT甲级真题解析」Advanced Level 1008 Elevator
    ELK之Logstash解析时间相差8h的问题
    Linux（八）——解压缩
    去重的方法
    蜜罐技术是什么？为什么黑客最怕踩到蜜罐?
    .NET周刊【11月第2期 2023-11-12】
    从0基础开发搜索引擎(一)-----实战项目
    程序员不撰写代码注释和文档的十大理由
    Node.js安装使用问题
  • 原文地址：https://blog.csdn.net/Crocodile1006/article/details/133464895