-
八大排序源码(含优化)
大家好,我是纪宁,这篇文章是关于八大排序的源代码,具体实现过程会在后续文章中介绍。1、直接插入排序
时间复杂度O(N^2),原数据越有序,效率越高。
当原数据有序时,则时间复杂度为O(N)。原数据倒序时,时间复杂度为O(N^2)
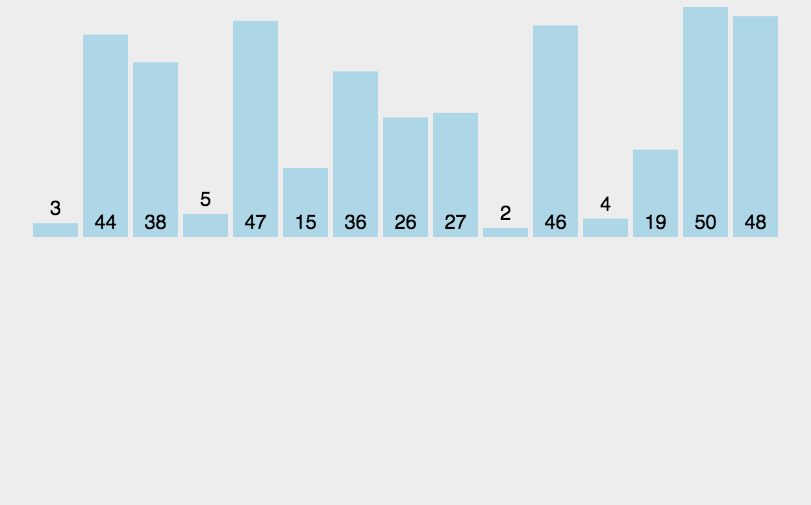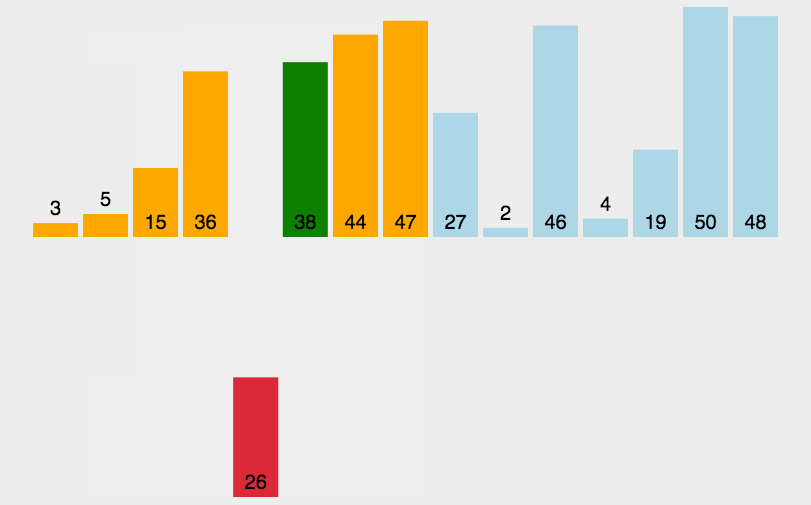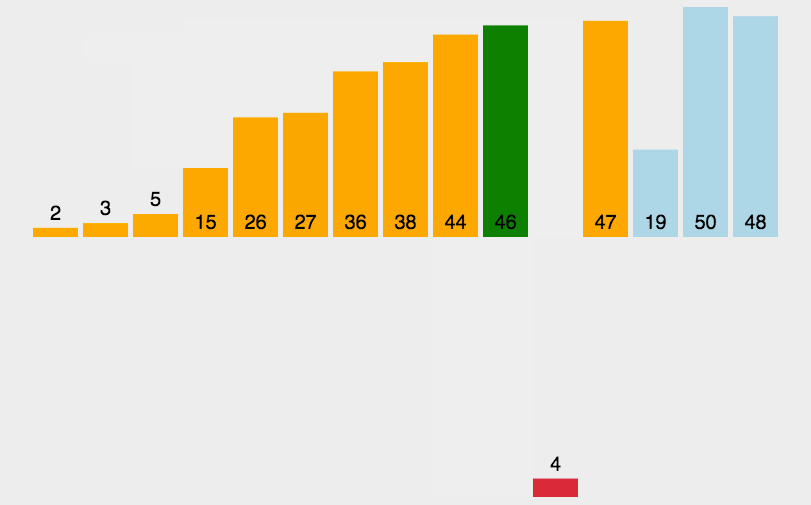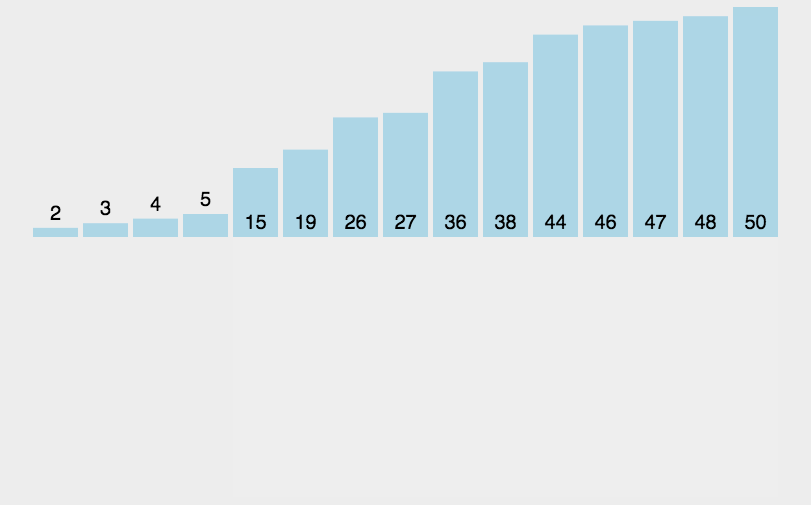
void InsertSort(int* a, int n)//直接插入排序 { for (int i = 0; i < n - 1; i++) { int end = i; int tmp = a[end+1]; while (end >= 0) { if (a[end] >tmp) { a[end + 1] = a[end]; } else { break; } end--; } a[end + 1] = tmp; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
2、希尔排序
时间复杂度:O(N^1.3) 空间复杂度:O(1)
希尔排序是插入排序的优化,整体思路是先预排序,使原数据更接近有序,等到gap==1时,就变成了直接插入排序。void ShellSort(int* arr, int n) { int gap = n; while (gap > 1) { gap = gap / 3 + 1;//gap也可以 /=2;奇特数字必须保证gap最后的值为1 for (int i = 0; i < n - gap; i++) { int end = i; int tmp = arr[end + gap]; while (end >= 0) { if (tmp < arr[end]) { arr[end + gap] = arr[end]; } else { break; } end -= gap; } arr[end + gap] = tmp; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
3、选择排序
时间复杂度:O(N^2) 空间复杂度:O(1)
每次选择一个最大或者最小的数,使其出现在正确的位置。

void SelectSort(int* a, int n) { for (int j = 0; j < n; j++) { int mini = j; int maxi= n - j-1; for (int i = j; i < n-j; i++) { if (a[i] < a[mini]) { mini = i; } if (a[i] > a[maxi]) { maxi = i; } } Swap(&a[mini], &a[j]); if (maxi == j) { maxi = mini;//最大值如果在 j 这个位置的话,结果这个位置被换成了min 的值 } Swap(&a[maxi], &a[n-1-j]); } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
4、冒泡排序
时间复杂度:O(N^2) 空间复杂度:O(1)
思路最简单的排序,所有程序员的白月光!
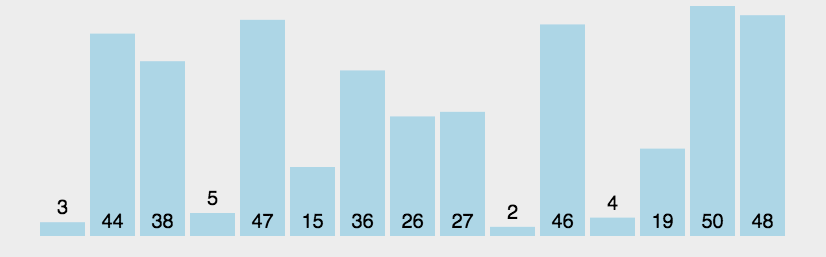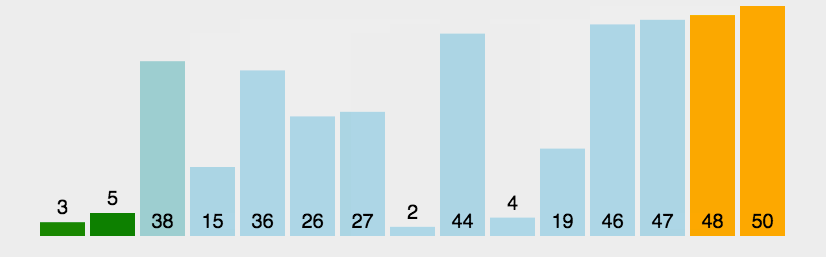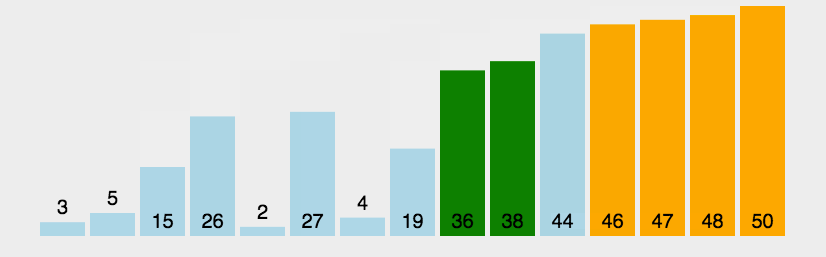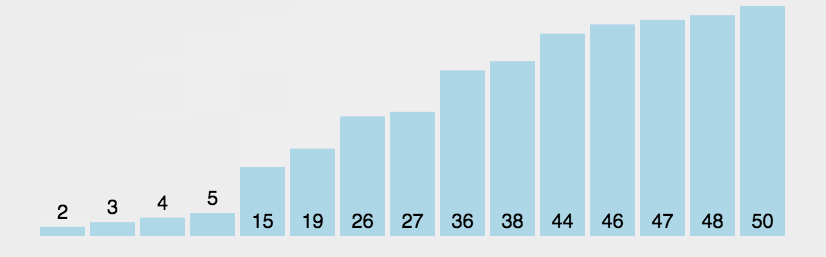
void BubbleSort(int* a, int n)//冒泡排序 { for (int i = 0; i < n; i++) { int ret = 0;//如果一趟后ret还等于0,说明数据已经有序 for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { Swap(&a[j], &a[j + 1]); ret = 1; } } if (ret == 0) break; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
5、堆排序
时间复杂度:O(N*logN) 空间复杂度:O(1)
建堆的时候可以采用向上调整和向下调整建堆,而排序的时候只能使用向下调整算法。
排升序建大堆,降序建小堆。void Adjustup(int* a, int child)//向上调整 { int parent = (child - 1) / 2; while (parent >= 0) { if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } else { break; } } } void Adjustdown(int* a, int parent, int n)//向下调整 { int child = 2 * parent + 1; while (child < n) { if (child + 1 < n && a[child + 1] > a[child]) { child++; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = 2 * parent + 1; } else { break; } } } void HeapSort(int* arr, int sz) { //第一步,建堆 向上调整建堆 //for (int i = 1; i < sz; i++) //{ // Adjustup(arr, i); //} //向下调整建堆 for (int i = (sz - 1) / 2; i >= 0; i--) { Adjustdown(arr, i, sz - 1); } int end = sz - 1; while (end > 0) { Swap(&arr[0], &arr[end]); Adjustdown(arr, 0, end); end--; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
6、快速排序
时间复杂度:O(N*logN) 空间复杂度:O(1)
快速排序递归实现
霍尔法

int QuickSortPart1(int*a,int left,int right)//霍尔版本 { int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2]));//三数取中 Swap(&a[left], Maxi);//换到最左边 int key = a[left]; int keyi = left; while (left<right) { while (left<right && a[right]>=key) { right--; } while (left < right && a[left] <= key) { left++; } Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[left]); return left; } void QuickSort(int*arr, int begin, int end) { if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排 { return; } int keyi = QuickSortPart1(arr, begin, end); /*int keyi = QuickSortPart2(arr, begin, end); int keyi = QuickSortPart3(arr, begin, end);*/ QuickSort(arr, begin, keyi - 1); QuickSort(arr, keyi + 1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
挖坑法
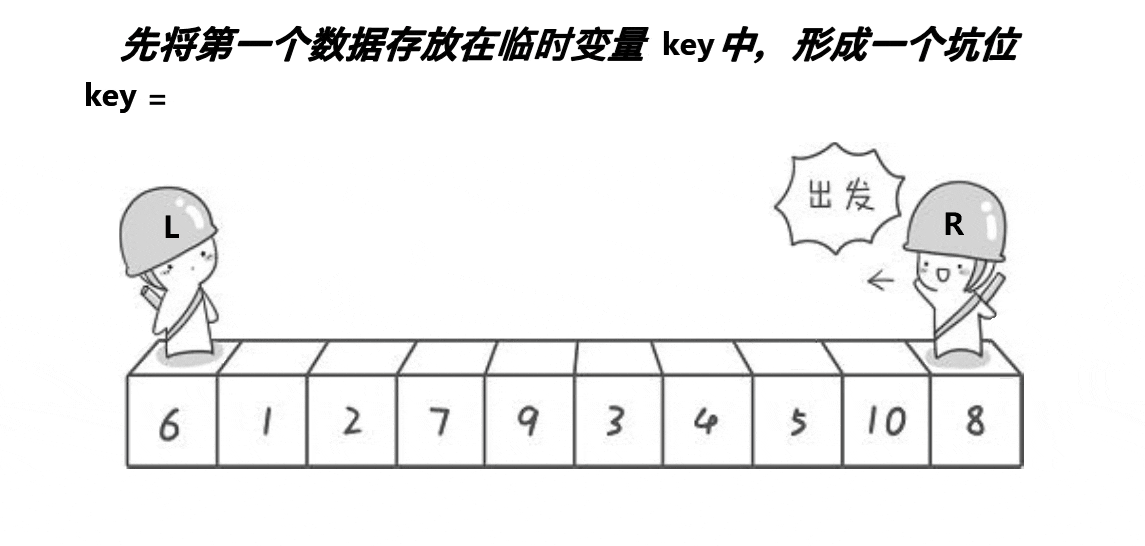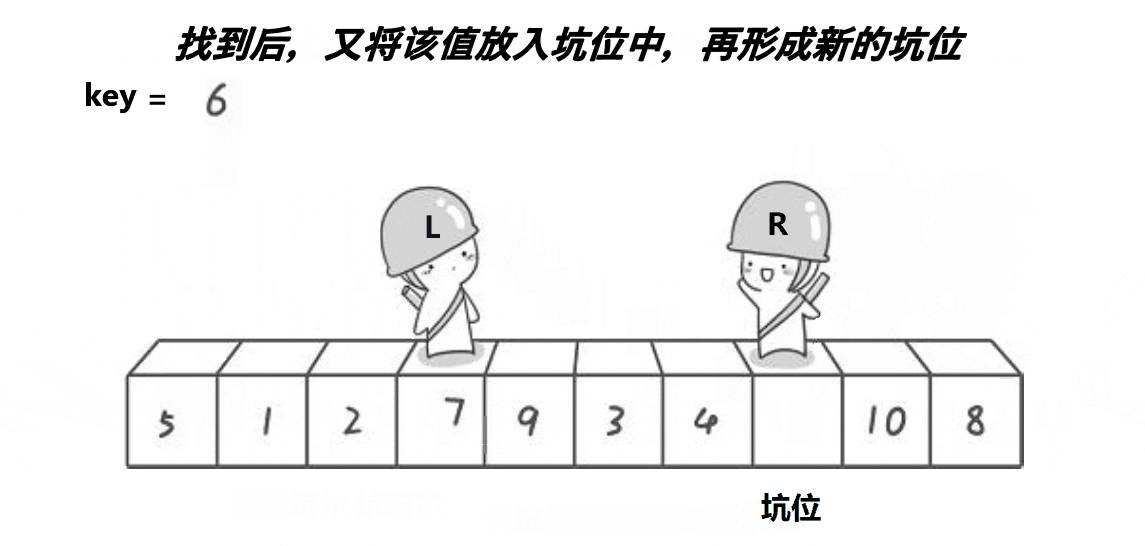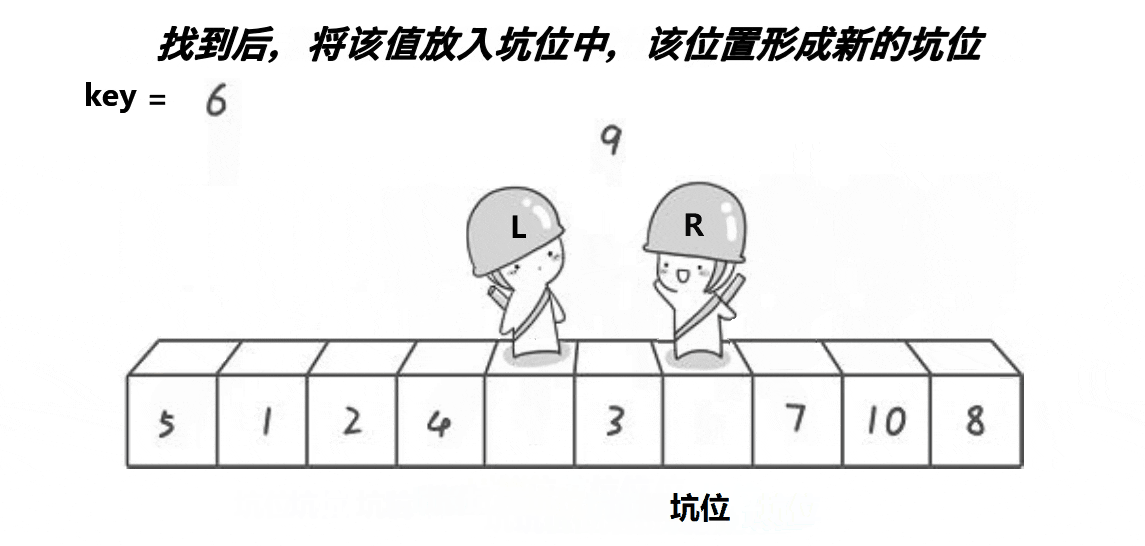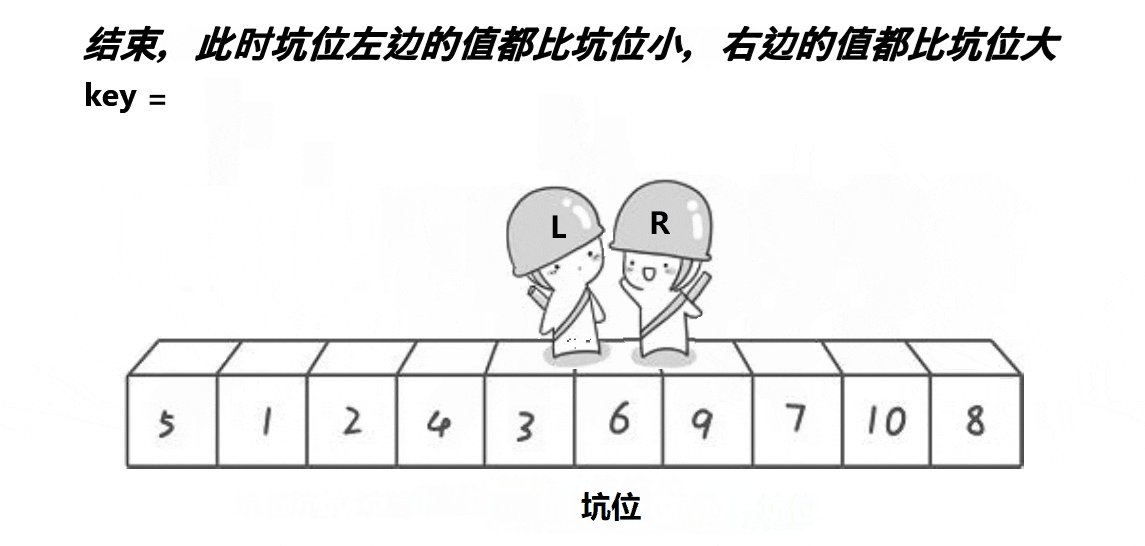
int QuickSortPart2(int* arr, int left, int right)//挖坑法 { int* Maxi = (&arr[left], &arr[right], &(arr[(left + right) / 2])); Swap(&arr[left], Maxi); int holei = left; int hole = arr[left]; while (left < right) { while (left < right && arr[right] >= hole) { right--; } arr[holei] = arr[right]; holei = right; while (left < right && arr[left] <= hole) { left++; } arr[holei] = arr[left]; holei = left; } arr[holei] = hole; return left; } void QuickSort(int*arr, int begin, int end) { if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排 { return; } /*int keyi = QuickSortPart1(arr, begin, end);*/ int keyi = QuickSortPart2(arr, begin, end); /*int keyi = QuickSortPart3(arr, begin, end);*/ QuickSort(arr, begin, keyi - 1); QuickSort(arr, keyi + 1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
前后指针法

int QuickSortPart3(int* a, int left, int right)//快排快慢指针 { int* Maxi = (&a[left], &a[right], &(a[(left + right) / 2])); Swap(&a[left], Maxi); int keyi = left; int prev = left; int cur = left+1; while (cur <= right) { if (a[cur] < a[keyi]&& ++prev!= cur) { Swap(&a[prev], &a[cur]); } cur++; } Swap(&a[prev],&a[keyi]); return prev; } void QuickSort(int*arr, int begin, int end) { if (begin >= end)//等于是只有一个数需要排,大于是没有数需要排 { return; } //*int keyi = QuickSortPart1(arr, begin, end);*/ //int keyi = QuickSortPart2(arr, begin, end); int keyi = QuickSortPart3(arr, begin, end); QuickSort(arr, begin, keyi - 1); QuickSort(arr, keyi + 1, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
快速排序小区间优化
void QuickSort1(int* a, int begin, int end) { if (begin >= end) return; // 小区间优化,小区间不再递归分割排序,降低递归次数 if ((end - begin + 1) > 10) { int keyi = PartSort3(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort1(a, begin, keyi - 1); QuickSort1(a, keyi + 1, end); } else { InsertSort(a + begin, end - begin + 1);//直接插入排序 } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
快速排序非递归实现
快排非递归要用栈来实现void QuickSortNorn(int* a, int begin, int end) { ST st;//创建数组栈 STInit(&st);//初始化栈 STPush(&st, end);//入栈 STPush(&st, begin);//入栈 while (!STEmpty(&st))//判空 { int left = STTop(&st);//取栈顶数据 STPop(&st);//出栈 int right = STTop(&st); STPop(&st); int keyi = QuickSortPart1(a, left,right); if (keyi + 1 < right) { STPush(&st, right); STPush(&st, keyi + 1); } if (keyi - 1 > left) { STPush(&st, keyi - 1); STPush(&st, left); } } STDestroy(&st);//销毁栈 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
7、归并排序
时间复杂度:O(N*logN) 空间复杂度:O(N)
归并排序递归实现
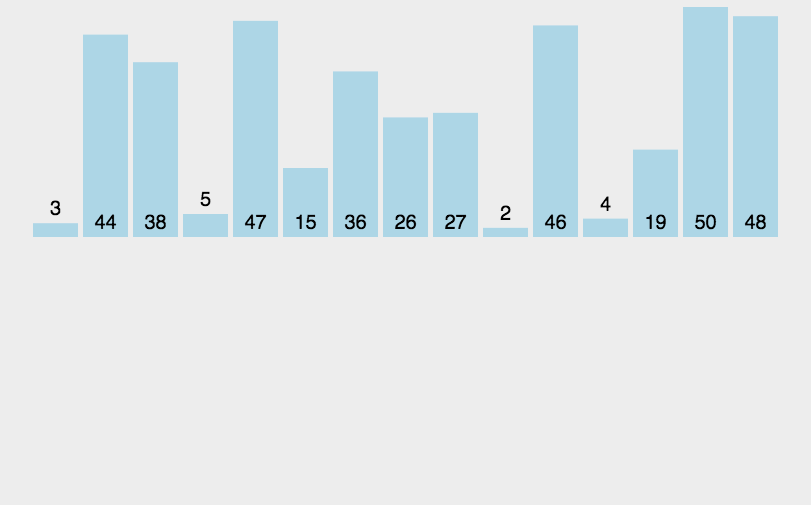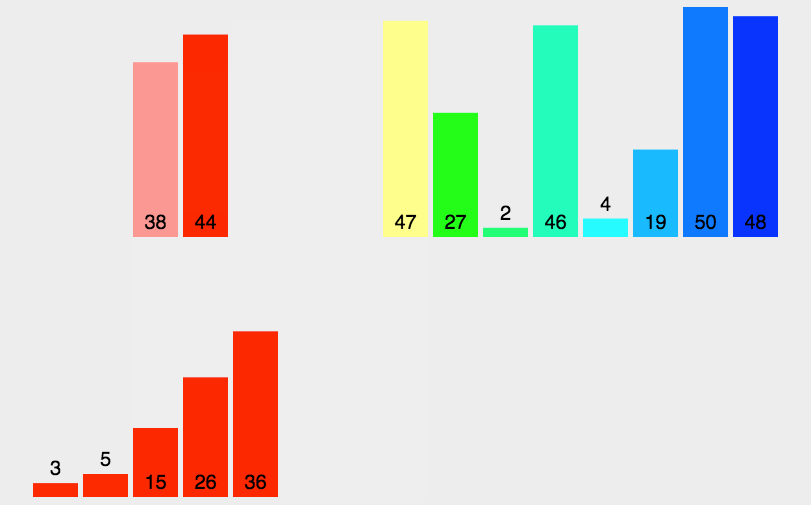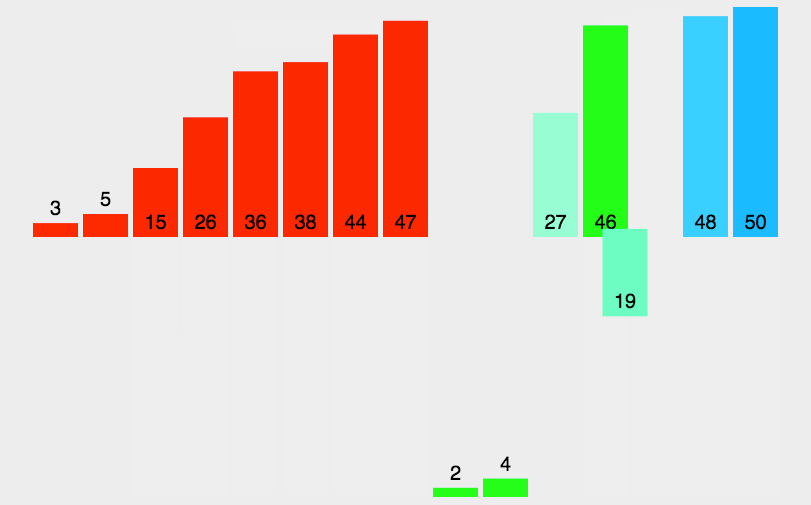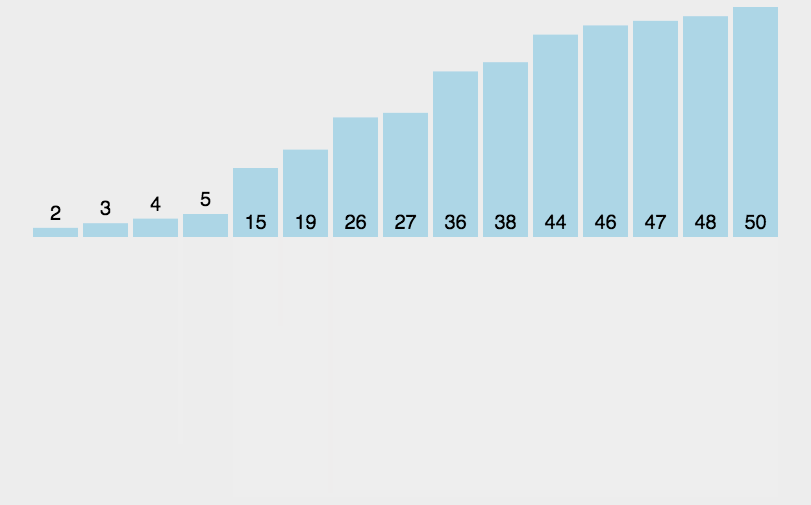
void _MergeSortPart(int* a, int* tmp, int begin, int end) { if (begin >= end) return; int midi = (begin + end) / 2; _MergeSortPart(a, tmp, begin, midi); _MergeSortPart(a, tmp, midi + 1, end); int begin1 = begin, end1 = midi; int begin2 = midi + 1, end2 = end; int index = begin; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[index++] = a[begin1++]; } else { tmp[index++] = a[begin2++]; } } while (begin1 <= end1) { tmp[index++] = a[begin1++]; } while (begin2 <= end2) { tmp[index++] = a[begin2++]; } memcpy(a+begin, tmp+begin, sizeof(int) * (end - begin + 1)); } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); _MergeSortPart(a, tmp, 0, n - 1); free(tmp); tmp = NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
归并排序非递归
void _MergeSortNonr(int* a, int* tmp, int begin, int end) { int gap = 1; while (gap <= end) { for (int i = 0; i <= end; i += 2 * gap) { int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; int index = i; if (begin2 > end) { break; } if (end2 > end) { end2 = end;//对范围进行修正 } while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[index++] = a[begin1++]; } else { tmp[index++] = a[begin2++]; } } while (begin1 <= end1) { tmp[index++] = a[begin1++]; } while (begin2 <= end2) { tmp[index++] = a[begin2++]; } memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));//拷贝回原数组 } gap *= 2; } } void MergeSortNonr(int* a, int n)//归并排序非递归 { int* tmp = (int*)malloc(sizeof(int) * n); _MergeSortNonr(a, tmp, 0, n - 1); free(tmp); tmp = NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
8、计数排序
时间复杂度:O(MAX(N,range)) 空间复杂度:O(range)
void CountSort(int* a, int n)//计数排序 { //先找最大值和最小值 int maxi = 0, mini = 0; for (int i = 1; i < n; i++) { if (a[i] > a[maxi]) { maxi = i; } if (a[i] < a[mini]) { mini = i; } } int max = a[maxi], min = a[mini]; int range = a[maxi] - a[mini]+1; int* count = (int*)malloc(sizeof(int) * range); memset(count, 0, sizeof(int) * range); for (int j = 0; j < n; j++) { count[a[j] - min]++; } int i = 0; for (int j = 0; j < n; j++) { while (count[j]--) { a[i++] = j + min; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
-
相关阅读:
服务器的维护是如何操作的
SpringCloud面试题及答案 300道,springcloud面试题总结 (持续更新)
贵金属金银铂铑钯回收-HP4080
微服务架构师封神之路13-RabbitMQ集群与高可用|RabbitMQ clustering and HA
说一说样式优先级的规则是什么?
linux系统打开终端自动执行:source .bashrc
MOSFET 和 IGBT 栅极驱动器电路的基本原理学习笔记(三)同步整流器驱动
手把手教你SSM整合(包教包会)
【机器学习网络】BP神经网络与深度学习-6 深度神经网络(deep neural Networks DNN)
目录授予777权限却还是无法进入的解决方案
- 原文地址:https://blog.csdn.net/zyb___/article/details/133456858
