【力扣周赛】第 364 场周赛⭐（前后缀分解+单调栈&DFS技巧）

竞赛链接

https://leetcode.cn/contest/weekly-contest-364/

Q1：2864. 最大二进制奇数（贪心）

https://leetcode.cn/problems/maximum-odd-binary-number/description/

提示：

1 <= s.length <= 100
s 仅由 '0' 和 '1' 组成
s 中至少包含一个 '1'

写法1——手动模拟（代码长，运行快）

贪心：最后一位保留一个 1，其余的 1 都放置在最开始的位置。

class Solution {
    public String maximumOddBinaryNumber(String s) {
        int n = s.length(), cnt = 0;
        char[] chs = s.toCharArray();
        for (int i = 0; i < n; ++i) {
            if (chs[i] == '1') ++cnt;
        }
        for (int i = 0; i < n; ++i) {
            if (i < cnt - 1) chs[i] = '1';
            else chs[i] = '0';
        }
        chs[n - 1] = '1';
        return new String(chs);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

写法2——API（代码短，运行慢）

public class Solution {
    public String maximumOddBinaryNumber(String s) {
        int cnt1 = (int) s.chars().filter(c -> c == '1').count();
        return "1".repeat(cnt1 - 1) + "0".repeat(s.length() - cnt1) + "1";
    }
}

1
2
3
4
5
6
7

Q2：2865. 美丽塔 I

https://leetcode.cn/problems/beautiful-towers-i/description/

提示：
1 <= n == maxHeights <= 10^3
1 <= maxHeights[i] <= 10^9

竞赛时代码——枚举山顶

计算每一个位置作为最高点时的最大结果，对所有结果取最大。

class Solution {
    public long maximumSumOfHeights(List<Integer> maxHeights) {
        long ans = 0;
        int n = maxHeights.size();
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, op(i, maxHeights));
        }
        return ans;
    }
    
    public long op(int k, List<Integer> maxHeights) {
        long ans = maxHeights.get(k);
        long l = maxHeights.get(k), r = maxHeights.get(k);
        for (int i = k - 1; i >= 0; --i) {
            l = Math.min(maxHeights.get(i), l);
            ans += l;
        }
        for (int i = k + 1; i < maxHeights.size(); ++i) {
            r = Math.min(maxHeights.get(i), r);
            ans += r;
        }       
        if (l <= 0 || r <= 0) return 0;
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Q3：2866. 美丽塔 II⭐⭐⭐（前后缀分解+单调栈）

https://leetcode.cn/problems/beautiful-towers-ii/description/

提示：

1 <= n == maxHeights <= 10^5
1 <= maxHeights[i] <= 10^9

数据范围大了一些。

解法

使用单调栈分别计算前缀和后缀递增段的元素最大和。

class Solution {
    public long maximumSumOfHeights(List<Integer> maxHeights) {
        int[] a = maxHeights.stream().mapToInt(i -> i).toArray();   // 列表转数组
        int n = a.length;
        long[] suf = new long[n + 1];
        Deque<Integer> stk = new ArrayDeque<>();    // 单调递增的单调栈
        stk.push(n);                                // 加入 n 作为哨兵
        long sum = 0;
        // 从后往前
        for (int i = n - 1; i >= 0; --i) {
            int x = a[i];
            while (stk.size() > 1 && x <= a[stk.peek()]) {
                int j = stk.pop();
                sum -= (long) a[j] * (stk.peek() - j);  // 删除之前加到sum中的
            }
            sum += (long) x * (stk.peek() - i);         // 从i到stk.peek()-1都是x
            suf[i] = sum;
            stk.push(i);
        }

        long ans = sum;
        stk.clear();
        stk.push(-1);
        // 从前往后
        long pre = 0;
        for (int i = 0; i < n; ++i) {
            int x = a[i];
            while (stk.size() > 1 && x <= a[stk.peek()]) {
                int j = stk.pop();
                pre -= (long) a[j] * (j - stk.peek());
            }
            pre += (long) x * (i - stk.peek());
            ans = Math.max(ans, pre + suf[i + 1]);
            stk.push(i);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

学习到的技巧

1. 撤销累加
2. 加入哨兵

相关题目列表📕

【算法】前后缀分解题单
【算法】单调栈题单（矩阵系列、字典序最小、贡献法）

Q4：2867. 统计树中的合法路径数目（⭐）🐂

https://leetcode.cn/problems/count-valid-paths-in-a-tree/description/

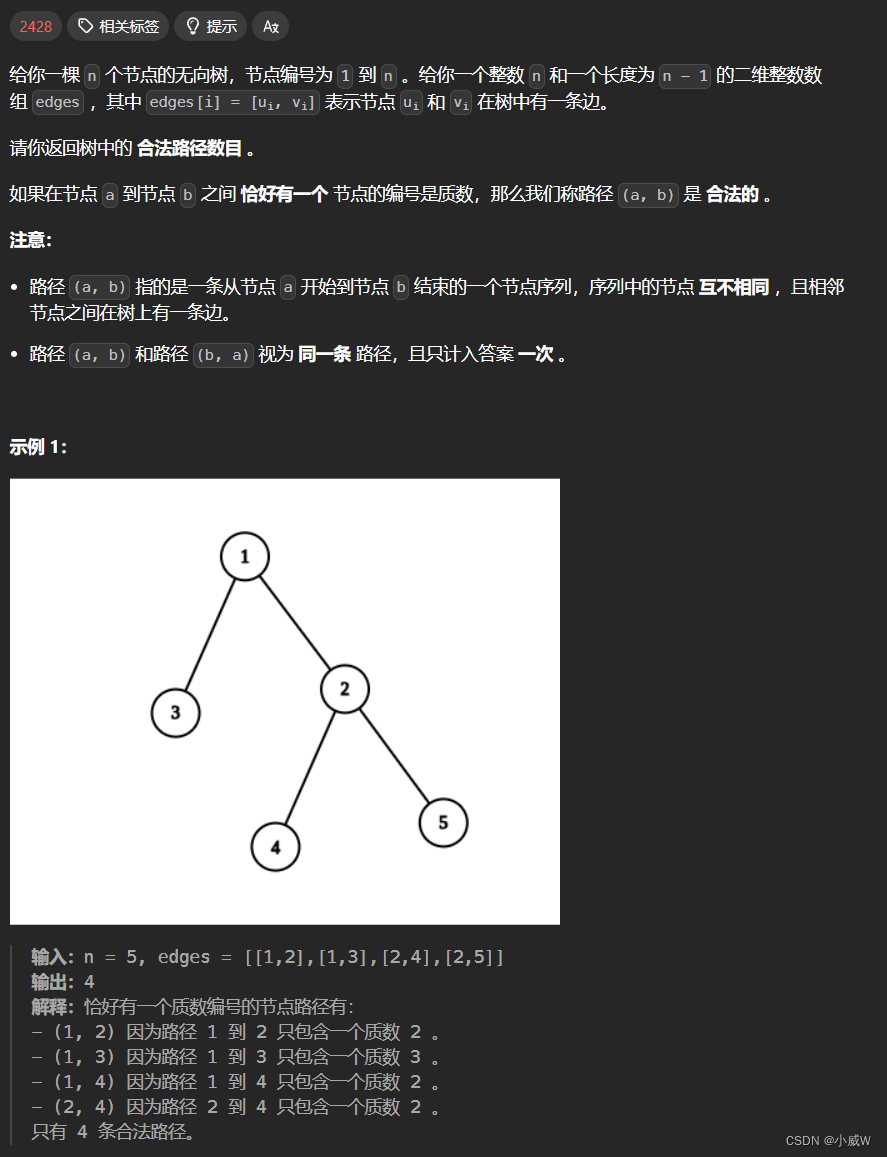
提示：
1 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
1 <= ui, vi <= n
输入保证 edges 形成一棵合法的树。

解法——枚举质数为根+DFS非质数连通块

枚举每个为质数的节点，将其当作根，向外延申，直至到达叶子节点或者其它质数节点。
这样可以获得多个连通块，各个连通块中只有非质数节点。
对各个连通块中的节点数量根据乘法原理，就可以得到以该质数为根节点的合法路径数目。

class Solution {
    final static int MX = (int)1e5;
    final static boolean[] np = new boolean[MX + 1];    // 质数false,非质数true

    static {
        np[1] = true;
        for (int i = 2; i <= MX / i; ++i) {
            if (!np[i]) {
                for (int j = i * i; j <= MX; j += i) {
                    np[j] = true;
                }
            }
        }
    }

    public long countPaths(int n, int[][] edges) {
        // 建树
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (int[] e: edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }

        long ans = 0;
        int[] size = new int[n + 1];
        List<Integer> nodes = new ArrayList<>();    // 记录一个连通块中的所有节点
        for (int x = 1; x <= n; ++x) {
            if (np[x]) continue;        // 如果不是质数，就跳过。
            int sum = 0;
            for (int y: g[x]) {         // 质数x将这棵树分成了若干个连通块
                if (!np[y]) continue;
                if (size[y] == 0) {     // y还没有被计算过
                    nodes.clear();
                    dfs(y, -1, g, nodes);
                    for (int z: nodes) size[z] = nodes.size();
                }
                ans += (long)size[y] * sum; // 与之前的连通块做乘法原理
                sum += size[y];
            }
            ans += sum;                 // 从x出发的路径
        }
        return ans;
    }

    // dfs过程是将这个连通块中的节点都放入nodes列表中
    void dfs(int x, int fa, List<Integer>[] g, List<Integer> nodes) {
        nodes.add(x);
        for (int y: g[x]) {
            if (y != fa && np[y]) {
                dfs(y, x, g, nodes);
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

学习到的技巧

1. dfs的过程将所有经过的节点放入一个列表中，这样就可以记录连通块的大小。
2. 为了防止重复计算某个节点，创建一个数组存储其是否被经历过即可，这里可以直接存储它所在连通块的大小。

相似题目——2242. 节点序列的最大得分

https://leetcode.cn/problems/maximum-score-of-a-node-sequence/description/

周赛题目本质上是求一种类似于「非质数-质数-非质数」的路径个数。
这两题的共同点在于「枚举中间」，请读者细细品味。

解法——枚举中间的边

建树的过程中，对于每个节点只保留与它相连的最大的那三条边即可。
建树之后，枚举每条边作为中间边的情况，更新最大值。

class Solution {
    public int maximumScore(int[] scores, int[][] edges) {
        int n = scores.length;
        List<int[]>[] g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList());
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            g[x].add(new int[]{scores[y], y});
            g[y].add(new int[]{scores[x], x});
        }
        for (int i = 0; i < n; ++i) {
            // 如果和i相连的点的数量>3，就可以删掉只剩3个最大的
            // 这样删可以确保和它组成一个序列的另外3个值都不会被删掉
            // 即对于序列a-x-y-b,枚举到x的时候要保证a,y,b都不会被删掉
            // 删去其它的边是为了后面遍历的时候快一些
            if (g[i].size() > 3) {
                g[i].sort((a, b) -> (b[0] - a[0]));     // 按照score从大到小排序
                g[i] = new ArrayList<>(g[i].subList(0, 3));
            }
        }

        int ans = -1;
        // 枚举每个边作为中间的边
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            for (int[] p: g[x]) {
                int a = p[1];       // x旁边的节点号a
                for (int[] q: g[y]) {
                    int b = q[1];   // y旁边的节点号b
                    if (a != y && b != x && a != b) {
                        ans = Math.max(ans, p[0] + q[0] + scores[x] + scores[y]);
                    }
                }
            }
        }
        return ans;
    }   
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

成绩记录

很差劲，脑子是糊掉的。