Matlab随机数的产生

目录

1、常见分布随机数的产生

1.1 二项分布

 1.2 泊松分布

1.3 几何分布

1.4 均匀分布（离散，等可能分布）

1.5 均匀分布（连续型等可能）

1.6 指数分布（描述“寿命”问题）

1.7 正态分布

1.8 三大抽样分布

1.8.1 χ2分布

1.8.2 t分布（Gosset 1908)

1.8.3 F 分布（Fisher,1924）

---

1、常见分布随机数的产生

1.1 二项分布

在贝努力试验中，某事件A发生的概率为p，重复该实验n次，X表示这n次实验中A发生的次数，则随机变量X服从的概率分布律（概率密度）为

记为    

binopdf(x,n,p)        pdf('bino',x,n,p)

返回参数为n和p的二项分布在x处的密度函数值（概率分布律值）。

>> clear
>> x=1:30;y=binopdf(x,300,0.05);
plot(x,y,'b*')

 binocdf(x,n,p)        cdf('bino',x,n,p)

 返回参数为n和p的二项分布在x处的分布函数值

>> clear
>> x=1:30;y=binocdf(x,300,0.05);
>> plot(x,y,'b+')

icdf('bino',q,n,p) 

  逆分布计算，返回参数为n和p的二项分布的分布函数当概率为q时的x值。

>> p=0.1:0.01:0.99;
>> x=icdf('bino',p,300,0.05);
>> plot(p,x,'r-')

R=binornd(n,p,m1,m2) 

产生m1行m2列的服从参数为n和p的二项分布的随机数据。 

>> R=binornd(10,0.5,3,4)
R =
     0     6     5     5
     6     6     5     5
     4     5     5     4
 
>> A=binornd(10,0.2,3)
A =
     1     2     2
     1     3     1
     2     2     2

 1.2 泊松分布

泊松分布描述密度问题：比如显微镜下细菌的数量X，单位人口里感染某疾病的人口数X，单位时间内来到交叉路口的人数X（或车辆数X），单位时间内某手机收到的信息的条数X，等等。

 X的分布律为（密度函数）

记为其中参数λ表示平均值。

poisspdf(x,lambda)           pdf('poiss',x,lambda)

 返回参数为lambda的泊松分布在x处的概率值。

>> clear
>> x=0:30;p=pdf('poiss',x,4);
>> plot(x,p,'b+')

 poisscdf(x,lambda)    cdf('poiss',x,lambda)

 返回参数为lambda的泊松分布在x处的分布函数值：

>> x=1:30;
>> p=cdf('poiss',x,5);
>> plot(x,p,'b*')

 poissrnd(lambda,m1,m2)

  返回m1行m2列的服从参数为lambda的泊松分布的随机数。

>> poissrnd(10,3,4)
 
ans =
 
    15    10     9     7
    14    10     7     9
    10     9    14    10
>> poissrnd(10,3)
 
ans =
 
    14    11     8
     8    11    13
     5    10    11

1.3 几何分布

在伯努利试验中，每次试验成功的概率为p，失败的概率为q=1-p,0

geopdf(x,p)

返回服从参数为p的几何分布在x处的概率值。 

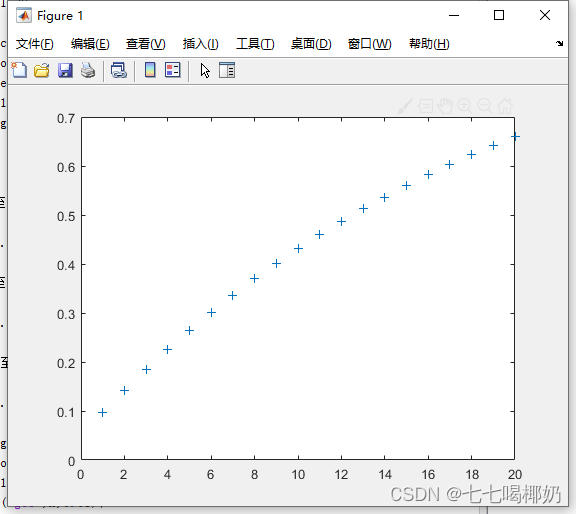
>> x=1:20;
>> p=geopdf(x,0.05);
>> plot(x,p,'*')

>> x=1:20;
>> p=cdf('geo',x,0.05);
>> plot(x,p,'+')

返回分布函数值

>> R=geornd(0.2,3,4)
R =
     0     0     5     0
     0     2     2     8
     9    10     0     0
>> R1=geornd(0.2,3)
R1 =
     0     8     1
     3     3     0
     0     0     1

1.4 均匀分布（离散，等可能分布）

 

>> x=1:20;
>> p=unidpdf(x,20);f=unidcdf(x,20);
>> plot(x,p,'*',x,f,'+')

 

>> R=unidrnd(20,3,4)
R =
     1    14     8    15
    17    16    14     1
    19    15     4     6
>> R=unidrnd(20,3)
R =
     1    14     1
     2     7     9
    17    20     8

1.5 均匀分布（连续型等可能）

 

>> clear
>> x=1:20;p=unifpdf(x,5,10);
>> p1=unifcdf(x,5,10);
>> plot(x,p,'r*',x,p1,'b-')

>> R=unifrnd(5,10,3,4)
R =
    8.8276    7.4488    8.5468    8.3985
    8.9760    7.2279    8.7734    8.2755
    5.9344    8.2316    6.3801    5.8131
 
>> R1=unifrnd(5,10,3)
R1 =
    5.5950    6.7019    8.7563
    7.4918    7.9263    6.2755
    9.7987    6.1191    7.5298

1.6 指数分布（描述“寿命”问题）

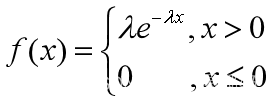
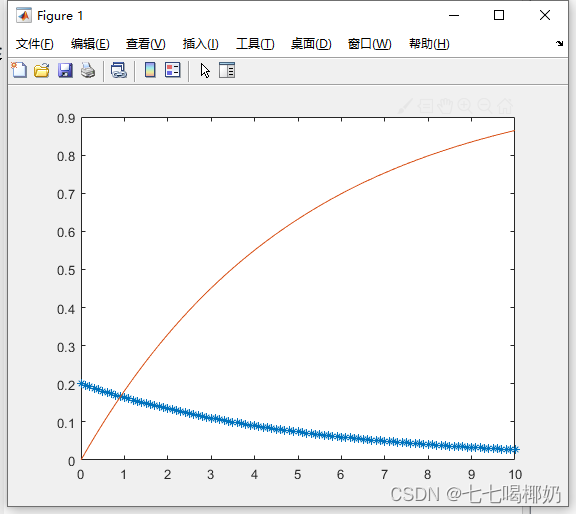
>> x=0:0.1:10;
p=exppdf(x,5);
p1=expcdf(x,5);
plot(x,p,'*',x,p1,'-')

>> R=exprnd(5,3,4)
R =
    1.7900    3.0146    6.7835    1.0272
    0.5776    9.8799    0.8675    7.0627
    0.2078    9.5092    6.8466    0.3668
 
>> R1=exprnd(5,3)
R1 =
    5.2493    2.4222    0.9267
    8.1330    3.7402    2.6785
    6.9098    5.2255    2.9917

1.7 正态分布

clear
x=-10:0.1:15;
p1=normpdf(x,2,4);p2=normpdf(x,4,4);p3=normpdf(x,6,4);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('mu=2'),gtext('mu=4'),gtext('mu=6')

clear
x=-10:0.1:15;
p1=normpdf(x,4,4);p2=normpdf(x,4,9);p3=normpdf(x,4,16);
plot(x,p1,'r-',x,p2,'b-',x,p3,'g-'),
gtext('sig=2'),gtext('sig=3'),gtext('sig=4')

>> clear
>> x=-10:0.1:10;
>> p=normcdf(x,2,9);
>> plot(x,p,'-'),gtext('分布函数')

>> p=[0.01,0.05,0.1,0.9,0.05,0.975,0.9972];
>> x=icdf('norm',p,0,1)
x =
-2.3263 -1.6449 -1.2816 
1.2816 -1.6449 1.96 2.7703

x=icdf('norm',p,0,1)

 计算标准正态分布的分布函数的反函数值，即知道概率情况下，返回相应的分位数。

产生正态分布的随机数

>> R=normrnd(0,1,3,4)
R =
    1.5877    0.8351   -1.1658    0.7223
   -0.8045   -0.2437   -1.1480    2.5855
    0.6966    0.2157    0.1049   -0.6669
>> R1=normrnd(0,1,3)
R1 =
    0.1873   -0.4390   -0.8880
   -0.0825   -1.7947    0.1001
   -1.9330    0.8404   -0.5445

1.8 三大抽样分布

卡方分布、t 分布和 F 分布也是统计学中常用的重要概率分布，它们分别用于解决以下问题：

1. 卡方分布在统计推断中经常用于分析类别型数据的关联性和拟合度。它可以帮助我们比较观察到的频数与期望频数之间的差异，并进行卡方检验来判断观察到的数据是否符合某种理论分布或假设。

2. t 分布在小样本情况下用于估计总体均值或进行假设检验。它通常用于推断均值、对比两个样本均值是否显著不同，或者构建置信区间等。t 分布具有允许样本量较小的特点，适用于样本标准差未知或总体不服从正态分布的情况。

3. F 分布常用于比较两个或多个总体方差的差异。它常用于方差分析（ANOVA）中，用于检验不同组或处理之间的方差是否显著不同。F 分布还被广泛应用于回归分析中的模型比较和变量选择。

1.8.1 χ2分布

X1,X2,…,Xn是一个来自服从标准正态分布总体的样本，则统计量(Helmert(1875),KarlPeason(1900))

服从自由度为n的卡方分布，记作

>> clear
>> x=0:0.1:10;
p1=chi2pdf(x,2);p2=chi2pdf(x,4);p3=chi2pdf(x,6);
>>plot(x,p1,'r*',x,p2,'b-',x,p3,'g--'),gtext('n=2'),gtext('n=4'),gtext('n=6')

1.8.2 t分布（Gosset 1908)

X,Y相互独立，则

>> x=-15:0.1:15;
p1=tpdf(x,2);p2=tpdf(x,8);p3=tpdf(x,16);
plot(x,p1,'*',x,p2,'-',x,p3,'--'),legend('n=2','n=8','n=16')

1.8.3 F 分布（Fisher,1924）

X,Y相互独立，则统计量

>> clear
>> x=0:0.1:20;
>> p1=fpdf(x,2,10);p2=fpdf(x,5,5);p3=fpdf(x,10,2);
>> plot(x,p1,'*',x,p2,'-',x,p3,'--'),legend('n1=2,n2=10','n1=5,n2=5','n1=10,n2=2')