基变换与矩阵对角化 - 码农知识堂

基变换与矩阵对角化

矩阵乘法的本质是映射坐标

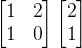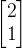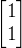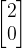$\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 的意思是把 $\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 映射到以 $\begin{bmatrix} 1\\ 1 \end{bmatrix}$ 和 $\begin{bmatrix} 2\\ 0 \end{bmatrix}$ 为基的向量空间中

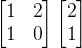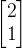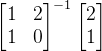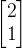$\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 表示将 $\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 展示成我们正常基向量空间中显示，而 $\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}^{-1}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 是将 $\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 用其本身的坐标系展示。

这也是基变换的本质，如果想对一组在 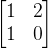$\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}$ 向量空间中的向量 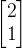$\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 进行旋转操作，旋转逆时针90度 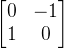$\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}$ ，则需要先将其转换为我们向量空间中显示，即 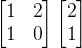$\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ ，然后再执行旋转操作 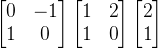$\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ ，最后再将它转变为自己的坐标系展示， $\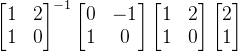begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}^{-1}\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}\begin{bmatrix} 2\\ 1 \end{bmatrix}$ 。

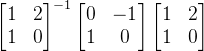$\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}^{-1}\begin{bmatrix} 0 & -1\\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 2\\ 1& 0 \end{bmatrix}$ 就是基变换。

特征向量是当基向量进行旋转，剪切，拉伸等操作后保持不变的向量

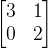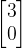$\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}$ 表示的是原来的基从 $\begin{bmatrix} 1\\ 0 \end{bmatrix}$ 拉伸成了 $\begin{bmatrix} 3\\ 0 \end{bmatrix}$ ， $\begin{bmatrix} 0\\ 1 \end{bmatrix}$ 变换成 $\begin{bmatrix} 1\\ 2 \end{bmatrix}$ ，变换过程中只发生拉伸，翻转操作的向量为特征向量。

因为特征向量在 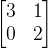$\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}$ 中映射只会发生拉伸，翻转，所以将特征向量作为基，进行基变换，特征向量为 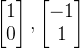$\begin{bmatrix} 1\\ 0 \end{bmatrix}, \begin{bmatrix} -1\\ 1 \end{bmatrix}$ ，基变换为 $\begin{bmatrix} 1 & -1\\ 0& 1 \end{bmatrix}^{-1}\begin{bmatrix} 3 & 1\\ 0& 2 \end{bmatrix}\begin{bmatrix} 1 & -1\\ 0& 1 \end{bmatrix}$ ，结果一定是对角矩阵，因为此变换本质只涉及拉伸，所以一定是对角矩阵。基变换矩阵是特征向量构成的，而特征向量是当前空间进行中间矩阵变换时不空间不变化的向量。所以把当前空间的变换转换到特征基的空间后，变换就变成了对基的放缩操作，也就是特征值构成的矩阵
相关阅读:
数组13— forEach() ：遍历数组元素
 yolov7简化网络yaml配置文件
 无人机+三维实景建模助力古建筑保护，传承历史记忆
 RabbitMq安装和Springboot整合
 如何打造独立站？这4个要点必须做到！
面对有挑战的事情
 Linux中的DNS服务搭建与管理
 使用grid来根据屏幕宽度计算每行可以放下多少个div盒子
 红队系列-溯源反制专题
 2022年信息安全工程师上午真题及答案解析
原文地址：https://blog.csdn.net/qq_36973725/article/details/133129646