【算法】滑动窗口破解长度最小子数组

Problem: 209. 长度最小的子数组

题意分析

首先来分析一下本题的题目意思

• 题目中会给到一个数组，我们的目的是找出在这个数组中 长度最小的【连续】子数组，而且要返回这个子数组的长度

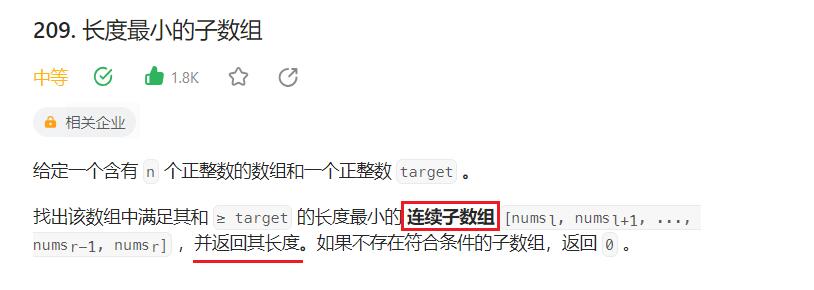
• 那我们首先来看示例1，在所找出的所有连续的子数组后，我们需要去比较谁的长度比较短一些，然后去选择短一些的这个子数组

• 下面们我们看这个示例3，其最后的返回长度为0，原因就在于给出的整型数组中所有数之和还是没有超过target，所以呢就返回了0

💬 但是要如何去寻找这个最小的子数组呢，我们马上来揭晓🖐

算法原理讲解

我们通过分析此题的算法原理来看看该如何去进行求解

暴力枚举O(N^2)

首先第一种，还是我们最熟悉的暴力解法

• 不过也是要使用到双指针的，我们从0的位置开始向后遍历

• 好，通过上面的这个图示，我们可以清晰地看出经过right的不断后移中，我们发现了一组长度> target的数据。但是呢我们这里使用的是【暴力枚举】，所以此时还会继续向后进行遍历操作→

---

可以观察到，当这个right继续后移将所遍历到的数加到sum上去的时候，虽然sum的大小是比target来得大了，但是呢这个len 的长度也相对应地发生可增长，这个其实的话就不对了，因为题目中所要求我们的是求解 最小子数组的长度

利用单调性，滑动窗口求解

看了上面的部分思路后，确实觉得暴力解法不可行，所以我接下去会使用【滑动窗口】的思想去做一个优化的操作

• 我们可以将left向后移动一位，此时子数组的和即为当前的sum减去left刚刚所指位置的那个数，即为【6】，那么我们在计算整个子数组的和时就可以不用让right重新开始遍历计算

💬 对于上面的这种 “同向移动的指针” 我们就称之为【滑动窗口】，读者可以看看下面的这个动图

那接下去呢我就来叙述一下如何使用【滑动窗口】的思想

1. 令left = 0, right = 0
2. 数据进窗口
3. 判断当前数据是否超过了目标值target
   1. 更新结果，数据出窗口
4. 继续循环往复

• 读者可以通过看下面的算法流程图，让后配合后面的代码，来思考这个滑动窗口的奇妙之处

💬 那有读者一定会问了，怎么能保证这个滑动窗口一定是正确的呢？

• 虽然在这里我们并没有像暴力枚举那样列出的可能性然后再去比较，但是呢我们可以知道接下来的情况枚举了也是白枚举，所以呢我们利用【单调性】，规避了很多没有必要的枚举行为

复杂度

• 时间复杂度:

对于时间复杂度, 等会读者在看代码的时候可以看到是存在两个嵌套的循环，所以就自认为是 $O(n^2)$，但是呢这里的时间复杂度应该是$O(n)$才对

• 我们通过看下面的这张图来理解一下，left和right指针在移动的时候都是一步步走的，当最后right指针移动到末尾结束的时候，我们考虑最坏的情况，就是两个指针分别都遍历了一遍这个数组，$2O(n)$时间复杂度即为 $O(n)$

• 空间复杂度:

没有开出任何多余的空间，那么空间复杂度即为$O(n)$

Code

以下即为滑动窗口的代码

• 注意最后在返回的时候要判断这个len是否有做更新，如果还是为最初的INT_MAX的话就不对了

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int sum = 0;
        int len = INT_MAX;
        for(int left = 0, right = 0; right < n; ++right)    
        {
            sum += nums[right];     // 进窗口
            while(sum >= target)
            {
                len = min(len, right - left + 1);   // 更新最短长度
                sum -= nums[left++];        // 出窗口
            }
        }
        return len == INT_MAX ? 0 : len;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18