[python 刷题] 42 Trapping Rain Water

[python 刷题] 42 Trapping Rain Water

题目：

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

这题的前置我觉得至少还是得做过 11 Container With Most Water 才好理解一些，毕竟两题的核心思路很像，都是获取容器中所能盛放的最大面积。

依旧以官方的例子来解释：height = [0,1,0,2,1,0,1,3,2,1,2,1]：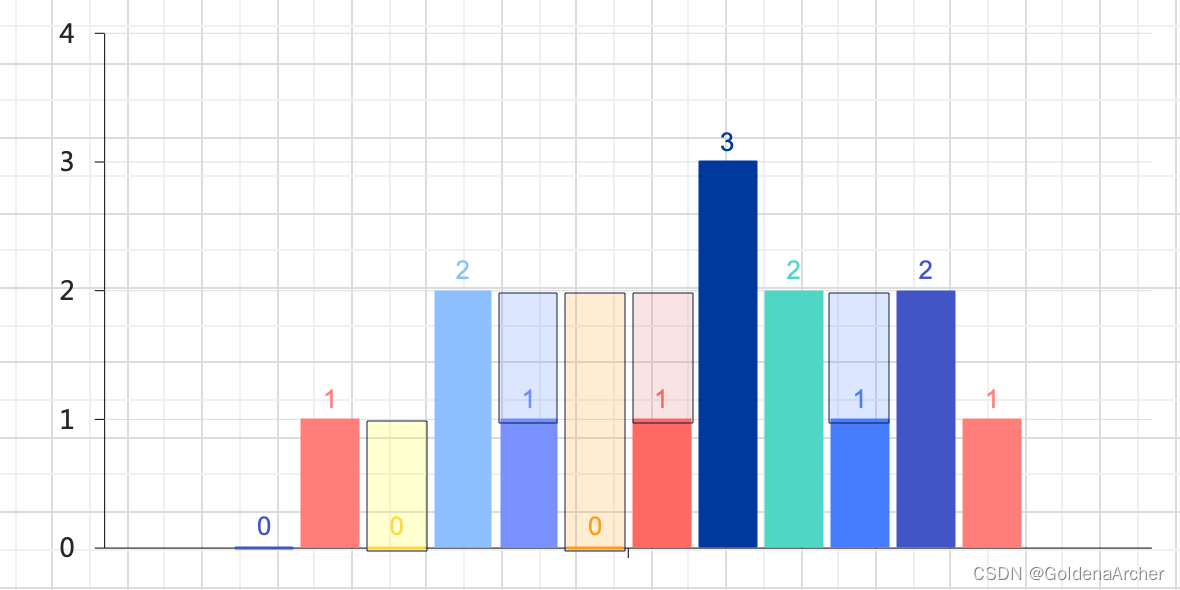

这里需要找到的就是两条立柱之间的凹陷的面积，即 $min(l,r)-h[i]$，$l$ 和 $r$ 可以视作 $h[i]$ 可能存在的最大立柱。对于 $h[i]$ 而言，它的面积为：对它而言最高的立柱，再减去其本身的面积。

其答案就为半透明方块的和：

最简单的一个思路是通过额外存储两个数组进行计算：

解法如下：

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0

        n = len(height)
        l_max = [0] * n
        r_max = [0] * n

        l_max[0] = height[0]
        for i in range(1, n):
            l_max[i] = max(l_max[i - 1], height[i])

        r_max[n - 1] = height[n - 1]
        for i in range(n - 2, -1, -1):
            r_max[i] = max(r_max[i + 1], height[i])

        return sum(min(l_max[i], r_max[i]) - height[i] for i in range(n))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

这里 min() 这块求的就是 min(l_max[i], r_max[i])，然后再求 min(l, r) - height[i] 的和

min(l_max[i], r_max[i]) - height[i] for i in range(n) 是一个 generator expression，会生成一个 generator object，也就是一个 iterable

sum() 会执行这个 iterable，并且返回相应的总和

这个解法的时间复杂度和空间复杂度都为 $O(n)$

一个可以做的油画是使用双指针保存 $l$ 和 $r$ 的下标，并且移动小的那个，如上篇笔记的图示：

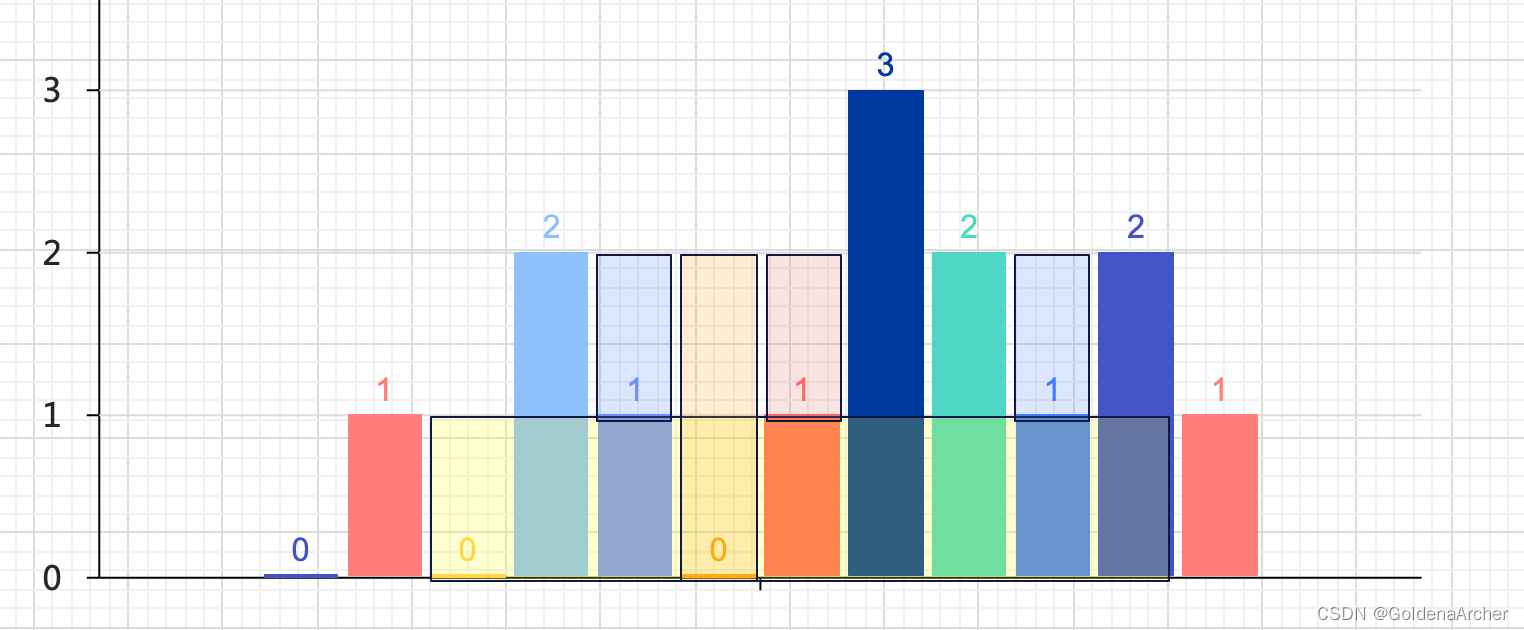
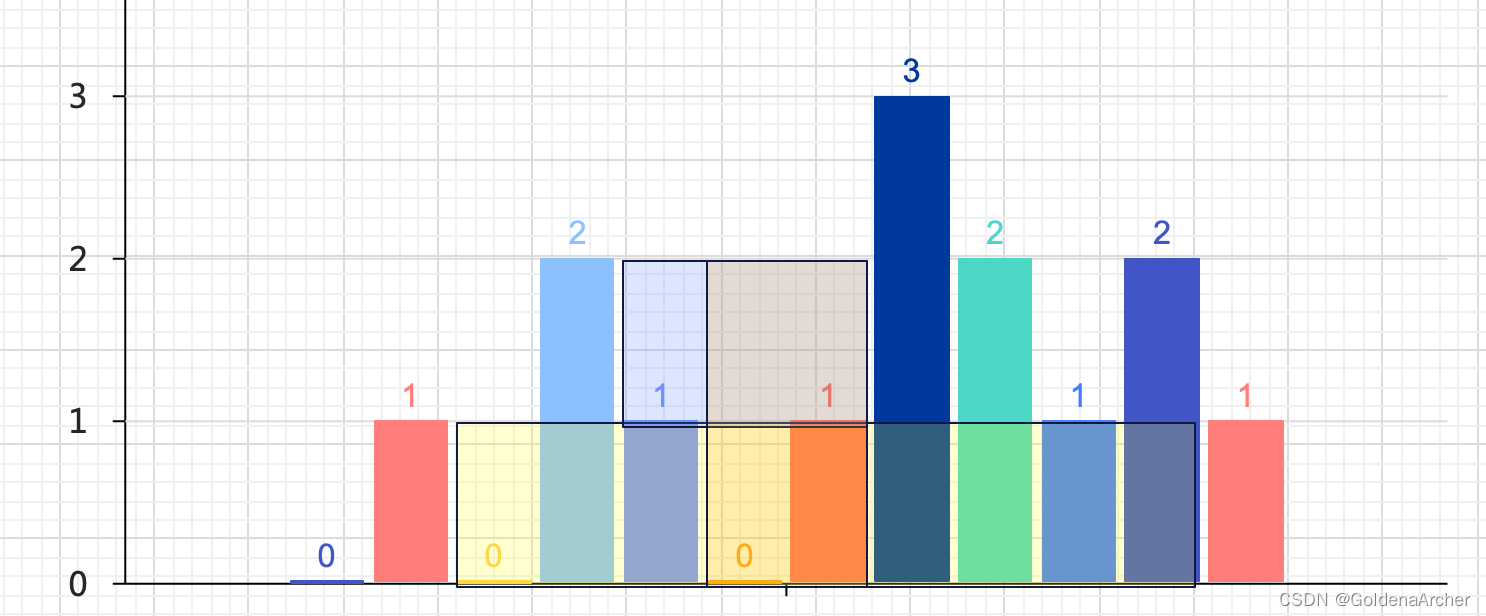
我稍微去掉了几个半透明的方块，这样看起来稍微清楚一点，本质上来说它的面积还是受限于较短的哪根立柱，因此可以沿用 11 Container With Most Water 的实现，代码如下：

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0

        l, r = 0, len(height) - 1
        l_max, r_max = height[l], height[r]
        res = 0

        while l < r:
            print(l_max, r_max)
            if l_max < r_max:
                l += 1
                l_max = max(l_max, height[l])
                res += l_max - height[l]
            else:
                r -= 1
                r_max = max(r_max, height[r])
                res += r_max - height[r]

        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

这个解法时间复杂度还是 $O(n)$，不过只遍历了一次，相对还是会比遍历三次快。空间复杂度则是从 $O(n)$ 优化到了 $O(1)$