【枚举+贪心】CF1409 E

Problem - E - Codeforces

题意：

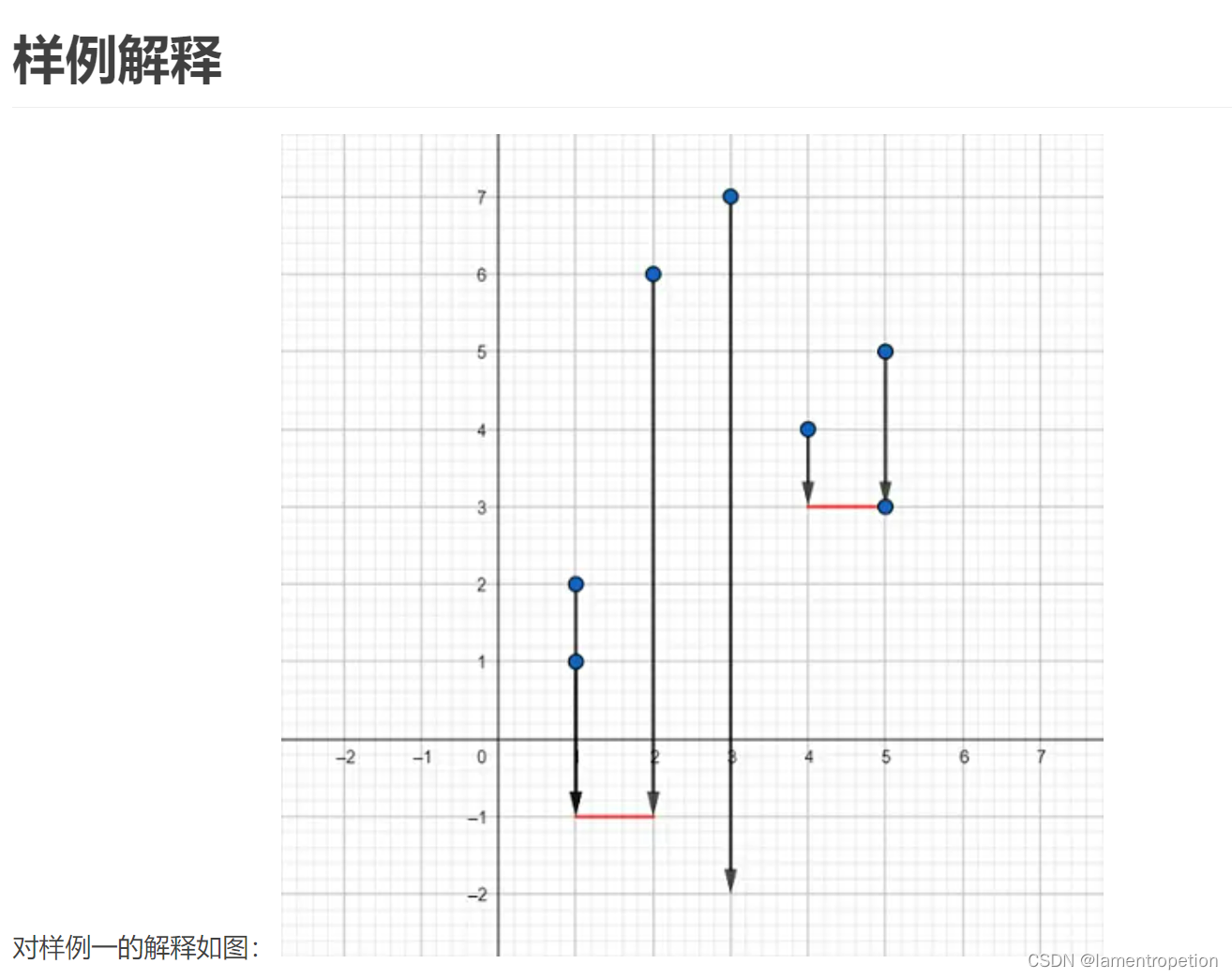
思路：

首先贪心的结论很明显，选两个贡献最大的区间

还有一个结论，这两个区间没有交点

然后就能直接做了，枚举一个区间，然后找这个区间后缀的最大贡献的区间即可，所以需要维护一个后缀贡献的最大值

Code：

#include 
 
#define int long long
 
using namespace std;
 
constexpr int N = 2e5 + 10;
constexpr int mod = 998244353;
 
int n, k;
int x[N], y[N];
int dp[N];
int mx[N];
 
void solve() {
    std::cin >> n >> k;
    for (int i = 0; i <= n + 1; i ++) {
        mx[i] = 0;
        dp[i] = 0;
    }
    for (int i = 1; i <= n; i ++) std::cin >> x[i];
    for (int i = 1; i <= n; i ++) std::cin >> y[i];
    
    std::sort(x + 1, x + 1 + n);
 
    for (int i = 1; i <= n; i ++) {
        int r = std::upper_bound(x + 1, x + 1 + n, x[i] + k) - x - 1;
        dp[i] = r - i + 1;
    }
 
    for (int i = n; i >= 1; i --) {
        mx[i] = std::max(mx[i + 1], dp[i]);
    }
 
    int ans = 0;
    for (int i = 1; i <= n; i ++) {
        ans = std::max(ans, dp[i] +  mx[i + dp[i]]);
    }
 
    std::cout << ans << "\n";
}
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
 
    int t = 1;
    std::cin >> t;
    while(t --) {
        solve();
    }
    return 0;
}