LeetCode 刷题记录——从零开始记录自己一些不会的（二）

20. 替换后的最长重复字符

• 题意

给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符，并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。

在执行上述操作后，返回包含相同字母的最长子字符串的长度。

• 思路

• 代码

class Solution {
public:
    int characterReplacement(string s, int k) {
        vector<int> num(26);
        int n = s.length();
        int maxn = 0;
        int left = 0,right = 0;
        while (right < n) {
            num[s[right]-'A'] ++;
            maxn = max(maxn,num[s[right]-'A']);
            if (right - left + 1 - maxn > k) {
                num[s[left]-'A'] --;
                left ++;
            }
            right ++;
        }
        return right - left;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

21. 最大宽度坡

• 题意

给定一个整数数组 A，坡是元组 (i, j)，其中 i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。

找出 A 中的坡的最大宽度，如果不存在，返回 0 。

• 思路

• 代码

class Solution {
public:
    int maxWidthRamp(vector<int>& nums) {
        stack<int> s;
        int res = 0;
        int n = nums.size();
        s.push(0);
        for (int i = 0;i < n;i ++) {
            if (s.empty()||nums[s.top()] > nums[i]) 
                s.push(i);
        }
        for (int j = n-1;j >= res;--j) {
            while (s.size()&&nums[s.top()] <= nums[j]) {
                int pos = s.top();
                s.pop();
                res = max(res,j - pos);
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

22. 销售利润最大化

• 题意

• 思路

区间合并+动态规划

• 代码

class Solution {
public:
    int maximizeTheProfit(int n, vector<vector<int>> &offers) {
        vector<vector<pair<int, int>>> groups(n);
        for (auto &offer: offers)
            groups[offer[1]].emplace_back(offer[0], offer[2]);

        vector<int> f(n + 1);
        for (int end = 0; end < n; end++) {
            f[end + 1] = f[end];
            for (auto &[start, gold]: groups[end])
                f[end + 1] = max(f[end + 1], f[start] + gold);
        }
        return f[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

23. 判断是否能拆分数组

• 题意

• 思路

• 代码

class Solution {
    public boolean canSplitArray(List<Integer> nums, int m) {
        //区间DP
        int n=nums.size();
        //f[i][j]:nums[i...j]能否拆分成合法数组
        boolean[][] f=new boolean[n][n];
        int[] pre=new int[n];
        pre[0]=nums.get(0);
        //构建前缀和数组
        for(int i=1;i<n;i++){
            pre[i]=pre[i-1]+nums.get(i);
        }
        for(int i=n-1;i>=0;i--){
            f[i][i]=true;
            if(i+1<n)   f[i][i+1]=true;
            for(int j=i+2;j<n;j++){
                //pre[j]-pre[i]表示sum(nums[i+1...j])
                //若sum(nums[i+1...j])>=m,那么nums[i...j]能否合法拆分取决于nums[i+1...j]能否合法拆分
                if(pre[j]-pre[i]>=m&&f[i+1][j]){
                    f[i][j]=true;
                }
                //pre[j]-pre[i]+nums.get(i)-nums.get(j)表示sum(nums[i...j-1])
                //这种写法可以防止数组越界
                //若sum(nums[i...j-1])>=m,那么nums[i...j]能否合法拆分取决于nums[i...j-1]能否合法拆分
                else if(pre[j]-pre[i]+nums.get(i)-nums.get(j)>=m&&f[i][j-1]){
                    f[i][j]=true;
                }else{
                    f[i][j]=false;
                }               
            }
        }
        return f[0][n-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

• 思路2

• 代码

class Solution {
public:
    bool canSplitArray(vector<int> &nums, int m) {
        int n = nums.size();
        if (n <= 2) return true;
        for (int i = 1; i < n; i++)
            if (nums[i - 1] + nums[i] >= m)
                return true;
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11

24. 找出最安全路径

• 思路

• 思路

二分+BFS

• 代码

// 二分 + BFS
int maximumSafenessFactor(vector<vector<int>> &grid) {
    typedef pair<int, int> P;
    const int N = 401;
    int n = grid.size();
    int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
    
    // 1.求每个点的安全系数，同上
    
    // 2.求最大安全系数
    // 2.1 check函数，检查是否存在结点安全系数均大于等于k的路径
    function<bool(int)> check = [&](int k) {
        bool f[n][n];
        memset(f, 0, sizeof f);
        queue<P> q;
        q.emplace(0, 0), f[0][0] = true;
        while (!q.empty()) {
            int x = q.front().first, y = q.front().second;
            q.pop();
            for (int i = 0; i < 4; i++) {
                int u = x + dx[i], v = y + dy[i];
                if (u < 0 || u >= n || v < 0 || v >= n ||
                    f[u][v] || d[u][v] < k)
                    continue;
                q.emplace(u, v), f[u][v] = true;
            }
        }
        return f[n - 1][n - 1];
    };
    // 2.2 二分
    int l = 0, r = min(d[0][0], d[n - 1][n - 1]), mid;
    while (l < r) {
        mid = (l + r + 1) >> 1;
        if (check(mid))l = mid;
        else r = mid - 1;
    }
    return l;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

• 思路2

• 代码

class Solution {
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public:
    int maximumSafenessFactor(vector<vector<int>> &grid) {
        int n = grid.size();
        vector<pair<int, int>> q;
        vector<vector<int>> dis(n, vector<int>(n, -1));
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j]) {
                    q.emplace_back(i, j);
                    dis[i][j] = 0;
                }
            }
        }

        vector<vector<pair<int, int>>> groups = {q};
        while (!q.empty()) { // 多源 BFS
            vector<pair<int, int>> nq;
            for (auto &[i, j]: q) {
                for (auto &d: dirs) {
                    int x = i + d[0], y = j + d[1];
                    if (0 <= x && x < n && 0 <= y && y < n && dis[x][y] < 0) {
                        nq.emplace_back(x, y);
                        dis[x][y] = groups.size();
                    }
                }
            }
            groups.push_back(nq); // 相同 dis 分组记录
            q = move(nq);
        }

        // 并查集模板
        vector<int> fa(n * n);
        iota(fa.begin(), fa.end(), 0);
        function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };

        for (int ans = (int) groups.size() - 2; ans > 0; ans--) {
            for (auto &[i, j]: groups[ans]) {
                for (auto &d: dirs) {
                    int x = i + d[0], y = j + d[1];
                    if (0 <= x && x < n && 0 <= y && y < n && dis[x][y] >= dis[i][j])
                        fa[find(x * n + y)] = find(i * n + j);
                }
            }
            if (find(0) == find(n * n - 1)) // 写这里判断更快些
                return ans;
        }
        return 0;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

无意中发现的大佬博客

多源BFS

LeetCode 75 精选面试必备的75道核心题目

1. 递增的三元子序列

• 题意

• 思路

树状数组+哈希

• 代码

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {
        int n = nums.size();
        if (n < 3) {
            return false;
        }
        int first = nums[0], second = INT_MAX;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            if (num > second) {
                return true;
            } else if (num > first) {
                second = num;
            } else {
                first = num;
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2. 盛最多水的容器

• 题意

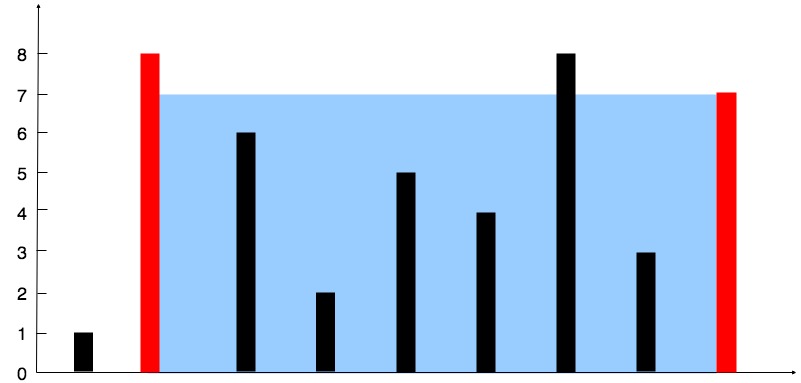
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

• 思路

• 代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1, res = 0;
        while(i < j) {
            res = height[i] < height[j] ? 
                max(res, (j - i) * height[i++]): 
                max(res, (j - i) * height[j--]); 
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

• 扩展 接雨水

  • 题意

  给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

  

  • 思路

  

  

  • 代码

  class Solution {
  public:
      int trap(vector<int>& height) {
          int n = height.size();
          if (n == 0) {
              return 0;
          }
          vector<int> leftMax(n);
          leftMax[0] = height[0];
          for (int i = 1; i < n; ++i) {
              leftMax[i] = max(leftMax[i - 1], height[i]);
          }
  
          vector<int> rightMax(n);
          rightMax[n - 1] = height[n - 1];
          for (int i = n - 2; i >= 0; --i) {
              rightMax[i] = max(rightMax[i + 1], height[i]);
          }
  
          int ans = 0;
          for (int i = 0; i < n; ++i) {
              ans += min(leftMax[i], rightMax[i]) - height[i];
          }
          return ans;
      }
  };
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26

  • 单调栈做法

  

  

  • 代码

  class Solution {
  public:
      int trap(vector<int>& height) {
          int ans = 0;
          stack<int> stk;
          int n = height.size();
          for (int i = 0; i < n; ++i) {
              while (!stk.empty() && height[i] > height[stk.top()]) {
                  int top = stk.top();
                  stk.pop();
                  if (stk.empty()) {
                      break;
                  }
                  int left = stk.top();
                  int currWidth = i - left - 1;
                  int currHeight = min(height[left], height[i]) - height[top];
                  ans += currWidth * currHeight;
              }
              stk.push(i);
          }
          return ans;
      }
  };
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23