数据结构与算法基础-(1)

 🌈write in front🌈
🧸大家好，我是Aileen🧸.希望你看完之后，能对你有所帮助，不足请指正！共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页：Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​
📣系列专栏：Aileen_0v0🧸的数据结构与算法学习系列专栏——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马~"

 

目录

1.1数据结构与算法的概念及介绍​编辑

 1.2时间复杂度(Time complexity)的引入

1.3时间复杂度和大O记法的练习

---

 

1.1数据结构与算法的概念及介绍🌱

 1.2时间复杂度(Time complexity)的引入🪴

算法1: 

#如果 a+b+c=1000, 且 a^2 + b^2 = c^2 (a,b,c 为自然数), 如何求出所有a,b,c 可能的组合
import time
start_time = time. time()
for a in range (0,1001):
    for b in range (0,1001):
        for c in range (0,1001):
            if a+b+c==1000 and a**2+b**2==c**2:
                print("a:",a,"b:",b,"c",c)
 
#获取时间
end_time = time. time()
print("所花费的时间:",(end_time - start_time))

 算法2: 

#如果 a+b+c=1000, 且 a^2 + b^2 = c^2 (a,b,c 为自然数), 如何求出所有a,b,c 可能的组合
import time
start_time = time. time()
for a in range (0,1001):
    for b in range (0,1001):
        c = 1000 - a - b
        if a**2+b**2==c**2:
            print("a:",a,"b:",b,"c",c)
 
#获取时间
end_time = time. time()
print("所花费的时间:",(end_time - start_time))

通过对比算法1和算法2 可知 单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的!程序的运行离不开计算机环境(包括硬件和操作系统) ~

这些客观原因会影响程序运行的速度并反应在程序的执行时间上。

那么如何才能客观的评判一个算法的优劣呢?

---

我们引入 时间复杂度

一个算法花费的时间与算法中语句的执行次数是成正比的。哪个算法语句执行的次数多，它花费的时间就多。

如何计算一个程序的执行次数:

 

注:下面代码示例都是将a+b+c的和记作n,进行执行次数的计算

      一段语句我们就粗略记作1次.

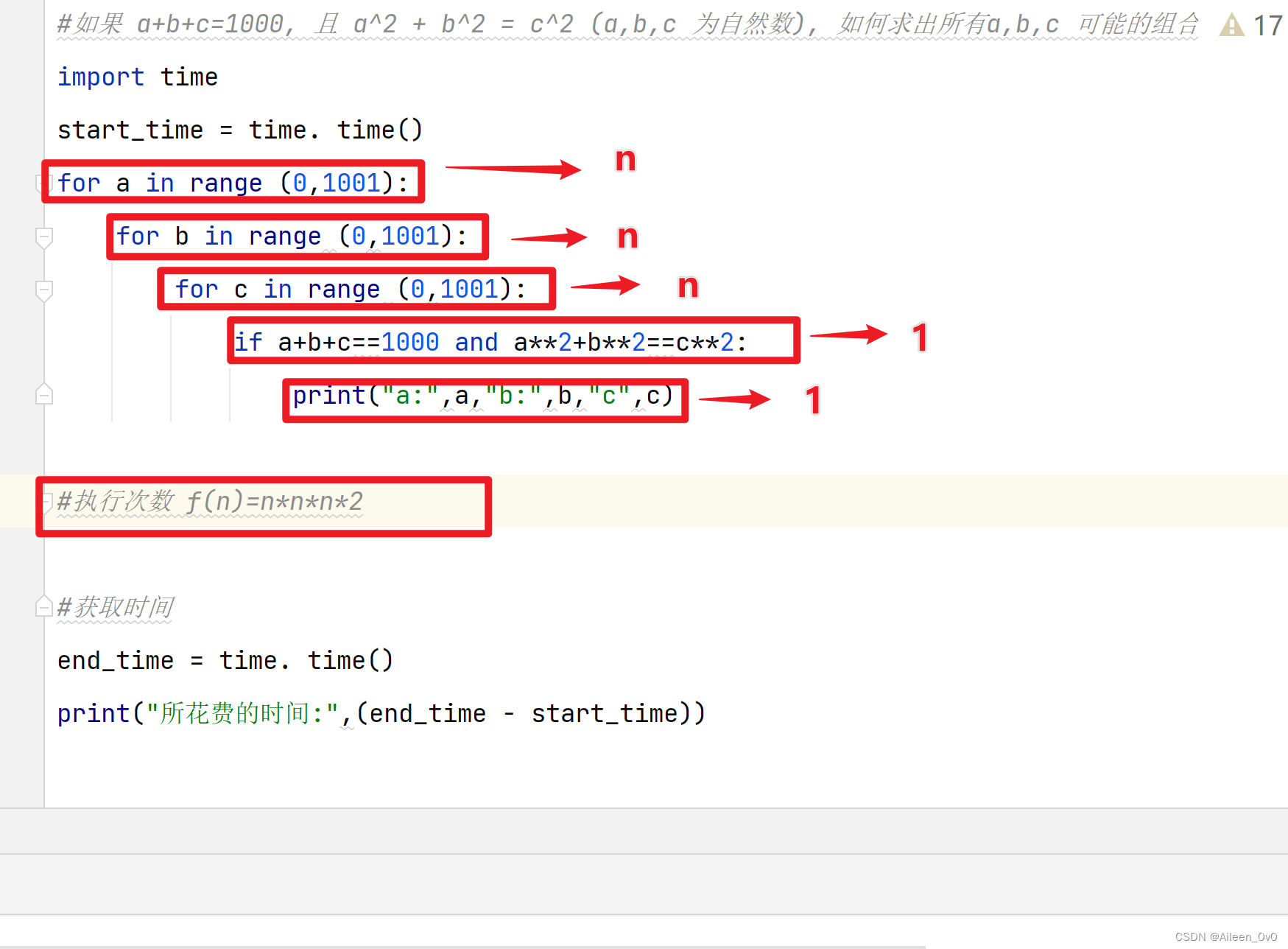
对于算法进行特别具体的细致分析虽然很好，但是实践中的实际价值有限。

对于算法最重要的是 数量级和趋势~~，这些是分析算法主要的部分。

对于算法最重要的是数量级和趋势，计量算法基本操作数量的规模函数中常量因子可以忽略不计。

通过比较 x^2 和 2x^2 的函数图像可知: 常量只影响陡峭程度，不影响趋势,而算法最重要的是数量级和趋势.

时间复杂度T(n)[Time complexity]:一个程序最终执行的次数来衡量算法的优劣-------eg: T(n)=2n^2
大o记法O(n)[Big O notation]:为时间复杂度的o渐进法（即忽略时间复杂度里面的常数）------eg: O(n)=n^2

T(n)=k*f(n)+c--->时间复杂度,  主要的影响因素就是n的大小
f(n)=n*n
f(n)叫做T(n)的渐进函数
T(n)=O(f(n))--->时间复杂度的O渐进法(大O技法)

如果时间复杂度T(n)=一个常数, 那么其大O记法 O(n)=O(1),因为 n 的最高次幂是 0

eg:T(n)=100100000,相当于T(n)= 100100000*n^0  那么 其O(n)=O(1)

 

1.3时间复杂度和大O记法的练习🌳

 Exercise:
1. Please write down the T(n) of the following code

2. What's the time complexity of it? (Big O notation)

🍁今天的学习笔记就分享到这里啦~🍁

🍁喜欢就一键三连支持一下吧♥~🍁

🍁谢谢家人们!🍁