矩阵论—凯莱-哈密顿定理

矩阵论—凯莱-哈密顿定理

凯莱-哈密顿定理内容

凯莱-哈密顿定理典型例题

典型例题

我们先来观察这个题目，题目要求 $A^{100}+2A^{50}$ ，若直接将矩阵A 代入计算，则会非常复杂，因此，这条路是走不通的。
我们试着引入我们今天介绍的凯莱-哈密顿定理来解这个题目。
令 $g(\lambda )=\lambda^{100}+2\lambda^{50}$ ，我们要求 $A^{100}+2A^{50}$ ，即求即可。
接下来我们确定矩阵A的特征多项式 $\phi (\lambda)$
$\phi (\lambda)=det(\lambda*I-A)=\begin{vmatrix} \lambda-1 &-1 & 1\\ -1& \lambda-1 & -1\\ 0& 1 & \lambda-2 \end{vmatrix}=\begin{vmatrix} \lambda & -\lambda& 2\\ -1& \lambda-1 &-1 \\ 0&1 &\lambda-2 \end{vmatrix}$
$=\lambda*(-1)^{1+1}\begin{vmatrix} \lambda-1&-1 \\ 1& \lambda-2 \\ \end{vmatrix}+(-1)*(-1)^{2+1}\begin{vmatrix} -\lambda &2 \\ 1& \lambda-2 \end{vmatrix}$
$=\lambda((\lambda-1)(\lambda-2)+1)+(-\lambda(\lambda-2)-2)$
$=\lambda(\lambda^{2}-3\lambda+3)-\lambda^{2}+2\lambda-2$
$=\lambda^{3}-4\lambda^{2}+5\lambda-2=\lambda^{3}-\lambda^{2}-3\lambda^{2}+5\lambda-2=\lambda^{2}(\lambda-1)-(3\lambda^{2}-5\lambda+2)$
$=\lambda^2(\lambda-1)-(\lambda-1)(3\lambda-2) =(\lambda-1)[\lambda^2-3\lambda+2]=(\lambda-1)^2(\lambda-2)$

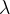设 $g(\lambda )=\phi (\lambda)q(\lambda)+b_0+b_1\lambda+b_2\lambda^2$ ，接下来确定系数：

用 $\lambda=1,2$ 分别带入上式，则有：
$g(1 )=\phi (1)q(1)+b_0+b_11+b_21^2 =b_0+b_1+b_2=3$ (1)
$g(2)=\phi (2)q(2)+b_0+b_12+b_22^2 =b_0+b_12+b_24=2^{100}+2^{51}$ (2)
对 $g(\lambda )$ 求关于 $\lambda$ 的微分，则有：
$g^{'}(\lambda ) = [2(\lambda-1)(\lambda-2)+(\lambda-1)^2]q(\lambda)+ \phi(\lambda)q^{'}(\lambda)+b_1+2b_2\lambda$
将 $\lambda=1$ 带入 $g^{'}(\lambda )$ ，则有：
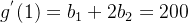$g^{'}(1)=b_1+2b_2=200$ (3)

联立(1)、(2)、(3)求解得出：
$b_0=2^{100}+2^{51}-400$
$b_1=606-2^{101}-2^{52}$
$b_2=-203+2^{100}+2^{51}$

于是有：
$A^{100}+2A^{50}=g(A)=b_0I+b_1A+b_2A^2$
相关阅读:
2500家门店倒闭：实体店败给电商已成定局？
牛客网——扫雷
 Python实现基于移动网络通讯行为的风险用户识别
 .NET高性能开发-位图索引（一）
Spring Boot中的max-http-header-size配置
 高并发场景下的分布式锁优化
 【数据库】MySQL分页查询
 基于Java+SpringBoot+Vue的图书借还小程序的设计与实现（亮点：多角色、点赞评论、借书还书、在线支付）
一些关于Netty的工作架构流程的问题
 【Docker 内核详解】namespace 资源隔离（五）：User namespaces
原文地址：https://blog.csdn.net/m0_48241022/article/details/133044250

凯莱-哈密顿定理典型例题