Routing路径系列数学建模(TSP+CVRP)

目录

1.Traveling Salesman Problem(TSP)

1.1 TSP数学模型

1.2 Gurobi测试

2.Capacitated Vehicle Routing Problem (CVRP)

2.1 CVRP数学模型

2.1.1 two-Index Vehicle Flow Formulation

2.1.2 three-Index Vehicle Flow Formulation

2.1.3 MTZ+CVRP模型

2.2 Gurobi测试 

3.Vehicle routing problems with time windows (VRPTW)

3.1 VRPTW模型

3.2 Solomon数据集测试

---

• 旅行商问题TSP：模型✅，代码✅
• 容量约束车辆路径规划问题：模型✅，代码✅
• 取送货车辆路径规划问题：模型，代码
• 时间窗约束车辆路径规划问题：模型✅，代码✅

 Gurobi求解代码https://github.com/bujibujibiuwang/Routing-Problem​​​​​​​

1.Traveling Salesman Problem(TSP)

1.1 TSP数学模型

参考：维基百科TSP

 给定一些城市和城市之间的距离，找到最短路径，经过每个城市最后返回起点，组合优化问题中属于NP-hard难度。对于TSP问题有两类混合整数规划模型：Miller–Tucker–Zemlin (MTZ)形式和Dantzig–Fulkerson–Johnson (DFJ)形式，DFJ模型更好，但是在某些特定条件下，MTZ模型仍然有用。两类模型有一些通用的符号。

     上述模型不能保证解中不出现子回路，我们只需要得到一个经过所有点的回路，有以下两种方式消除子回路。

• Miller–Tucker–Zemlin formulation(MTZ)

• Dantzig–Fulkerson–Johnson formulation(DFJ) 

 两种形式的完整数学模型如下：

1.2 Gurobi测试

官方资料Traveling Salesman Problem

用求解器DFJ模型，比较难处理的是子圈消除约束，指数量级的约束，因此使用回调函数来查找违反的子圈约束并将它们作为惰性约束添加到模型中。子圈消除代码如下：

# 子圈消除约束：callback + lazy constraints
def sub_tour_eliminate(model, where):
    # 如果当前优化状态为找到新的MIP解
    if where == GRB.Callback.MIPSOL:
        # 获取当前解
        values = model.cbGetSolution(model._vars)
        selected = gp.tuplelist((i, j) for i, j in model._vars.keys() if values[i, j] > 0.5)
        # 找到最小的圈
        cycle = get_sub_tour(selected)
        # 如果最小的圈长度不等于节点数，表明是子圈，将该圈的子圈消除约束添加到模型中
        if len(cycle) < number:
            model.cbLazy(gp.quicksum(model._vars[i, j] for i, j in combinations(cycle, 2)) <= len(cycle) - 1)
 
 
# 找到最小的子圈，用于添加lazy constraints
def get_sub_tour(edges):
    unvisited = [p.index for p in points]
    cycle = edges[:]
    while unvisited:
        current_cycle = []
        neighbors = unvisited
        while neighbors:
            current = neighbors[0]
            current_cycle.append(current)
            unvisited.remove(current)
            neighbors = [j for i, j in edges.select(current, '*') if j in unvisited]
        if len(current_cycle) < len(cycle):
            cycle = current_cycle
    return cycle

berlin52 instance求解结果如下，能找到最优解7544

Optimal solution found (tolerance 1.00e-04)
Best objective 7.544365901904e+03, best bound 7.544365901904e+03, gap 0.0000%

2.Capacitated Vehicle Routing Problem (CVRP)

参考：维基百科VRP

VRP问题描述：给定一组客户点、车辆容量、车辆数量、起始点和终点，目标是找到使得所有客户点都被访问一次的最短路径方案，这是TSP问题的扩展。

VRP变种：

• Vehicle Routing Problem with Pickup and Delivery (VRPPD)：具有提货和交付的车辆路径规划问题。有一组车辆需要从仓库或起始点出发，分别访问一系列提货地点以收集货物，然后将货物交付到相应的交付地点，最终返回仓库或结束点。问题的目标通常是最小化总行驶距离、时间或成本，或者在满足一定的约束条件下，找到一组最佳的路线方案
• Capacitated Vehicle Routing Problem (CVRP)：容量限制车辆路径规划问题。在CVRP中，每辆车辆都有一个限定的最大携带容量
• Vehicle Routing Problem with Time Windows (VRPTW)：带有时间窗口的车辆路径规划问题。在VRPTW中必须在每个配送地点的时间窗口内完成配送。时间窗口表示了在一定的时间范围内必须到达每个客户或配送地点，以满足客户的需求

2.1 CVRP数学模型

参考：Comparison between LP bound of the Two-Index and the Three-Index Vehicle Flow Formulation for the Capacitated Vehicle Routing Problem

​​​​​​​CVPR有多种建模方式，下面介绍了two-Index Vehicle Flow Formulation 和 three-Index Vehicle Flow Formulatiom以及基于MTZ的CVRP模型，使用Gurobi测试了第3种模型。

2.1.1 two-Index Vehicle Flow Formulation

该模型中变量数为，个等式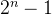，个不等式，共个约束

2.1.2 three-Index Vehicle Flow Formulation

 

2.1.3 MTZ+CVRP模型

VRP问题相比TSP，不同在于中心点可以多次访问，因此只需要在模型中把起点约束修改，再增加容量约束，使用MTZ或者DFJ方法消除子圈即可。使用MTZ方法，增加一个虚拟变量表示流经该点的流量，即能控制顺序也能确保车辆容量约束。

给定所有点的位置，客户点的需求，设定可用车辆数，所有车都有相同的容量限制，要求安排车辆运输路线实现总距离最小。

2.2 Gurobi测试 

在VRP数据集上测试，数据集给定了每个点的位置和需求，以及可使用车辆数和车载最大容量，下面是MTZ+CVRP模型的部分代码：

    """
    (2)决策变量和目标函数
    """
    model = gp.Model('VRP')
    select = model.addVars(edges, vtype=GRB.BINARY, name='select')
    flow = model.addVars(customers, vtype=GRB.CONTINUOUS, name='flow')
    model.setObjective(select.prod(distance), GRB.MINIMIZE)
    """
    (3)约束条件
    """
    # 每个客户点一条出边
    model.addConstrs(gp.quicksum(select[i, j] for j in points if j != i) == 1 for i in customers)
    # 每个客户点一条入边
    model.addConstrs(gp.quicksum(select[i, j] for i in points if i != j) == 1 for j in customers)
    # 流量顺序约束
    model.addConstrs((select[i, j] == 1) >> (flow[i] + points_list[j].demand == flow[j])
                     for i, j in edges if i != 0 and j != 0)
    # 流量大小约束
    model.addConstrs(points_list[i].demand <= flow[i] for i in customers)
    model.addConstrs(flow[i] <= vehicle_capacity for i in customers)
    # 车辆数量约束
    model.addConstr(gp.quicksum(select[0, j] for j in customers) <= vehicle_count)
    model.addConstr(gp.quicksum(select[i, 0] for i in customers) <= vehicle_count)

在16个点，3辆车，90容量的测试样例下求解最优解为278

Optimal solution found (tolerance 1.00e-04)
Best objective 2.787262997478e+02, best bound 2.787262997478e+02, gap 0.0000%

3.Vehicle routing problems with time windows (VRPTW)

3.1 VRPTW模型

VRPTW问题和CVRP相比，还要求车辆到达每个客户点的时间要在规定范围内，因此在CVRP模型基础上增加时间窗约束即可。

决策变量有三个：（1） 代表路径选择的0-1变量（2）消除子圈约束的流量（3）限制时间窗的开始时间

约束条件和CVRP模型相同，只是增加了时间窗约束

3.2 Solomon数据集测试

使用Solomon基准数据集验证模型，时间窗约束代码如下：

model.addConstrs(start[i] + int(distance[(i, j)]) + time[i] - BigM * (1 - select[i, j]) <= start[j] for i, j in edges if j != 0)
model.addConstrs(start[i] >= points_list[i].ready for i in points)
model.addConstrs(start[i] <= points_list[i].due for i in points)

其中C101样例，100个点的求解结果最优值为828，与官方最优解828.94一致

Optimal solution found (tolerance 1.00e-04)
Best objective 8.289368669428e+02, best bound 8.289368669428e+02, gap 0.0000%
route0:[0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 75, 0]
route1:[0, 13, 17, 18, 19, 15, 16, 14, 12, 0]
route2:[0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0]
route3:[0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0]
route4:[0, 43, 42, 41, 40, 44, 46, 45, 48, 51, 50, 52, 49, 47, 0]
route5:[0, 57, 55, 54, 53, 56, 58, 60, 59, 0]
route6:[0, 67, 65, 63, 62, 74, 72, 61, 64, 68, 66, 69, 0]
route7:[0, 81, 78, 76, 71, 70, 73, 77, 79, 80, 0]
route8:[0, 90, 87, 86, 83, 82, 84, 85, 88, 89, 91, 0]
route9:[0, 98, 96, 95, 94, 92, 93, 97, 100, 99, 0]