[PyTorch][chapter 55][GAN- 3]

前言：

     这里面主要结合GAN 损失函数，讲解一下JS散度缺陷问题。

---

目录：

1.  GAN 优化回顾
2.  JS 散度缺陷

---

一   GAN 优化回顾

        1.1 GAN 损失函数

              

                                                     

      1.2 固定生成器G,最优鉴别器 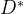为

               

                   此刻优化目标为

                  

                    

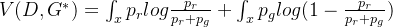
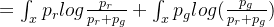
   1.3 得到最优鉴别器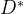后，最优编码器G为

             优化目标：

               

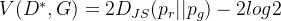
           当 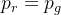, 得到最优解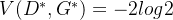

                

---

二  JS 散度缺陷：

  JS散度全称Jensen-Shannon散度，简称JS散度。

 性质： 非负性，对称性。

 2.1  问题：

        当两个分布完全不重叠时，JS散度为恒定值 log2.此时JS散度将无法产生有效的梯度信息无法更新生成网络的参数，从而出现网络训练困难的现象 ,

     当两个分布出现重叠时，JS散度采会平滑变动，产生有效梯度信息；

     当完全重合后，JS散度取得最小值0.如下图所示，红色的曲线分割两个正态分布，由于两个分布没有重叠，生成样本位置处的梯度值始终为0.
 

以下面两个p,q分布的例子： 

   

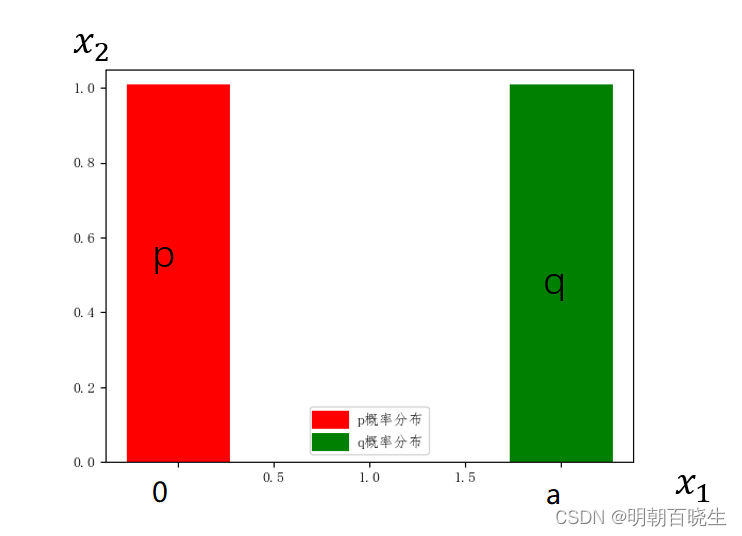
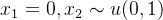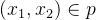
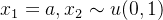              分布时候，

              分布时候，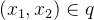

     2.2 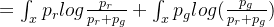 散度问题

             当 a=0,两者重叠

              当 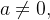 两者不重叠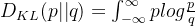

               

                                    

                                     

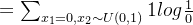
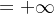
              同样 

  

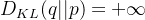
   2.3 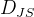 散度问题：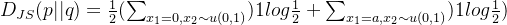

            

           当 a= 0时：

                

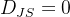
          当 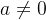 时：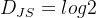

              

    

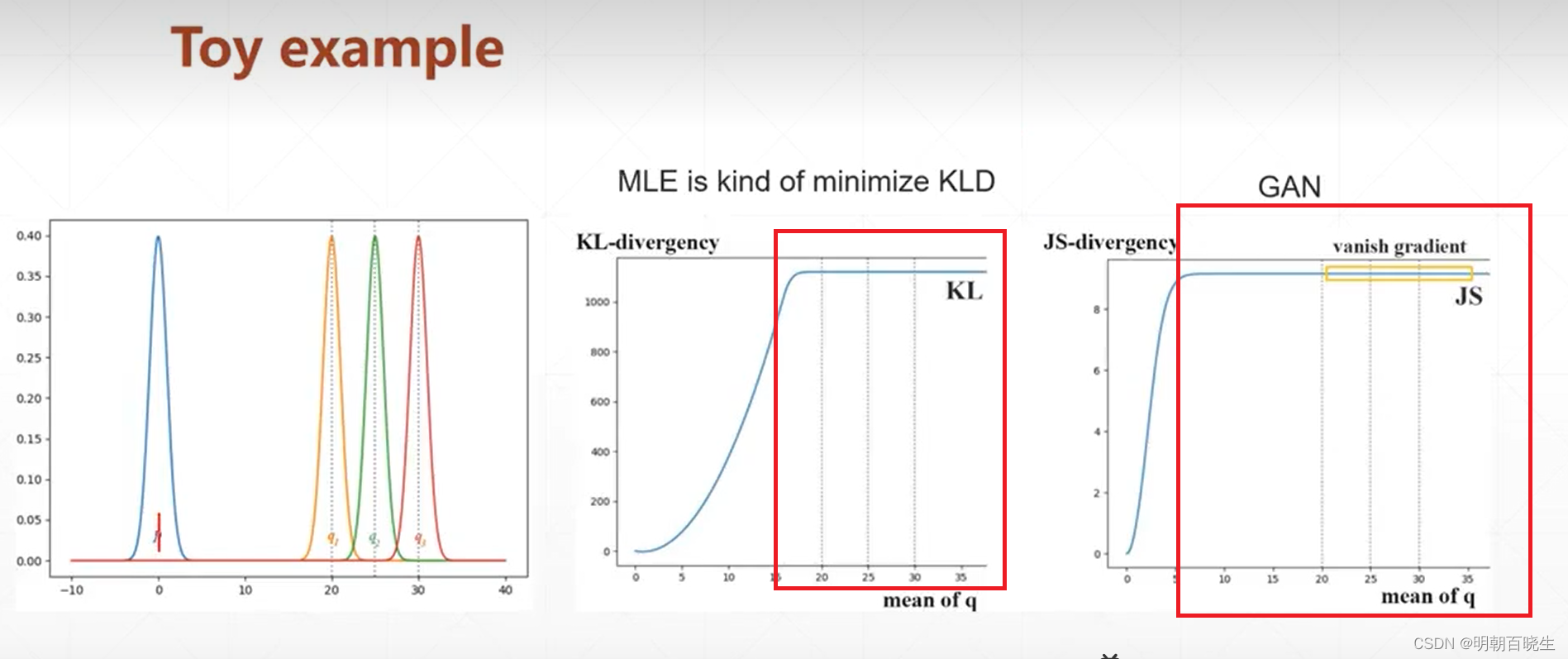
          两个分布完全不重叠时:JS散度为恒定值log2⁡,将无法产生有效的梯度信息；

         两个分布出现重叠时: JS散度采会平滑变动，产生有效梯度信息；

         完全重合后:JS散度取得最小值0,得到最优的生成器G

      如下图所示，红色的曲线分割两个正态分布，由于两个分布没有重叠，生成样本位置处的梯度值始终为0，无法更新生成网络的参数，从而出现网络训练困难的现象
 

   如下例子：

 当开始训练的时候，一旦进入了红色区域，KL,JS散度都是常数，此刻梯度为0

无法更新生成器G

 

参考：

 深度学习之生成对抗网络（7）WGAN原理_炎武丶航的博客-CSDN博客
链接：算法面试高频知识点：JS散度解析_牛客网

课时124 JS散度的缺陷_哔哩哔哩_bilibili

课时125 EM距离_哔哩哔哩_bilibili

课时124 JS散度的缺陷_哔哩哔哩_bilibili