【初阶数据结构】二叉树的几种遍历详解

君兮_的个人主页

勤时当勉励 岁月不待人

C/C++ 游戏开发

Hello,米娜桑们，这里是君兮_，有了我们之前介绍的树结构与二叉树的基础概念，今天我们来讲讲对二叉树的基本使用——遍历

一.二叉树的创建

• 我们自己先简单链式连接几个结点来创建一个二叉树方便我们之后对遍历的讲解

typedef struct BinaryTreeNode
{
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
    int val;
}BTNode;
//初始化
BTNode* BuyNode(int x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        perror("malloc fail");
        exit(-1);
    }
    node->val = x;
    node->left = node->right = NULL;
    return node;
}
int main()
{
  
    //手动构建
    BTNode* node1 = BuyNode(1);
    BTNode* node2 = BuyNode(2);
    BTNode* node3 = BuyNode(3);
    BTNode* node4 = BuyNode(4);
    BTNode* node5 = BuyNode(5);
    BTNode* node6 = BuyNode(6);
    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;
    int size = TreeLeafSize(node1);
    printf("%d", size);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

• 好了，有了这个基本的二叉树，我们正式开始我们今天的主要内容

---

二. 二叉树的遍历

1.前序遍历

• 什么叫前序遍历？
  抛开定义简单点来说，就是先访问根节点，再访问左子树，最后访问右子树 这种遍历方式就叫做前序遍历

void PrevOrder(BTNode* root)
{
    if (root == NULL)
        return;
    printf("%d ", root->val);

    PrevOrder(root->left);
    PrevOrder(root->right);

}
1
2
3
4
5
6
7
8
9
10

• 好了，这样我们这里就讲完了，来看看其他的遍历方式…
• 此时你可能一头雾水，我讲了什么吗？如讲，没错这里的代码只有这短短的几行却暗藏玄只因，我们来详细的分析一下上面的代码在干嘛

if (root == NULL)
        return;
1
2

• 首先，当这个二叉树为空或者程序遍历完二叉树后，我们就直接return，这点不难理解

	printf("%d ", root->val);
    PrevOrder(root->left);
    PrevOrder(root->right);

1
2
3
4

• 然后我们打印了此时这个结点的值(注意，这里的打印该值就是相当于访问了这个结点)
• 最后我们又递归调用了这个函数，并先传入该结点的左子树，最后又传入该结点的右子树
• 这里还是有点不明所以，我们在干嘛？但是你仔细观察一下，这里的执行顺序是不是很像我们刚才讲的前序遍历的特点 该结点->该结点的左子树->该结点的右子树 我们画图来解释一下
• 这里有如下的一个二叉树
  
• 我们现在来前序遍历一下
  
• 经过图中的一轮遍历，我们已经遍历完根结点和根结点的左子树了，下面我们要遍历根1的右子树
  
• 通过我们上面的分析，我们得知，当我们前序遍历这个二叉树时，打印在屏幕上的结果应该是 1 2 3 4 5 6
• 我们来测试一下我们的结果
  

2.中序遍历

• 啥叫中序遍历呢？
• 根据上面我们对前序遍历的简单解释，我们也可以相应的给中序遍历一个类似的解释
  当遍历时，先访问左子树再访问根结点最后访问右子树称为中序遍历

void InOrder(BTNode* root)
{
    if (root == NULL)
        return;
   
   InOrder(root->left);
   printf("%d ", root->val);
   InOrder(root->right);
}
1
2
3
4
5
6
7
8
9

• 仔细观察我们发现，中序遍历和前序遍历非常类似，那就是访问的顺序，中序先递归左子树，然后访问根结点，最后再递归右子树，我们还是通过上面那个例子来画图讲解一下
  
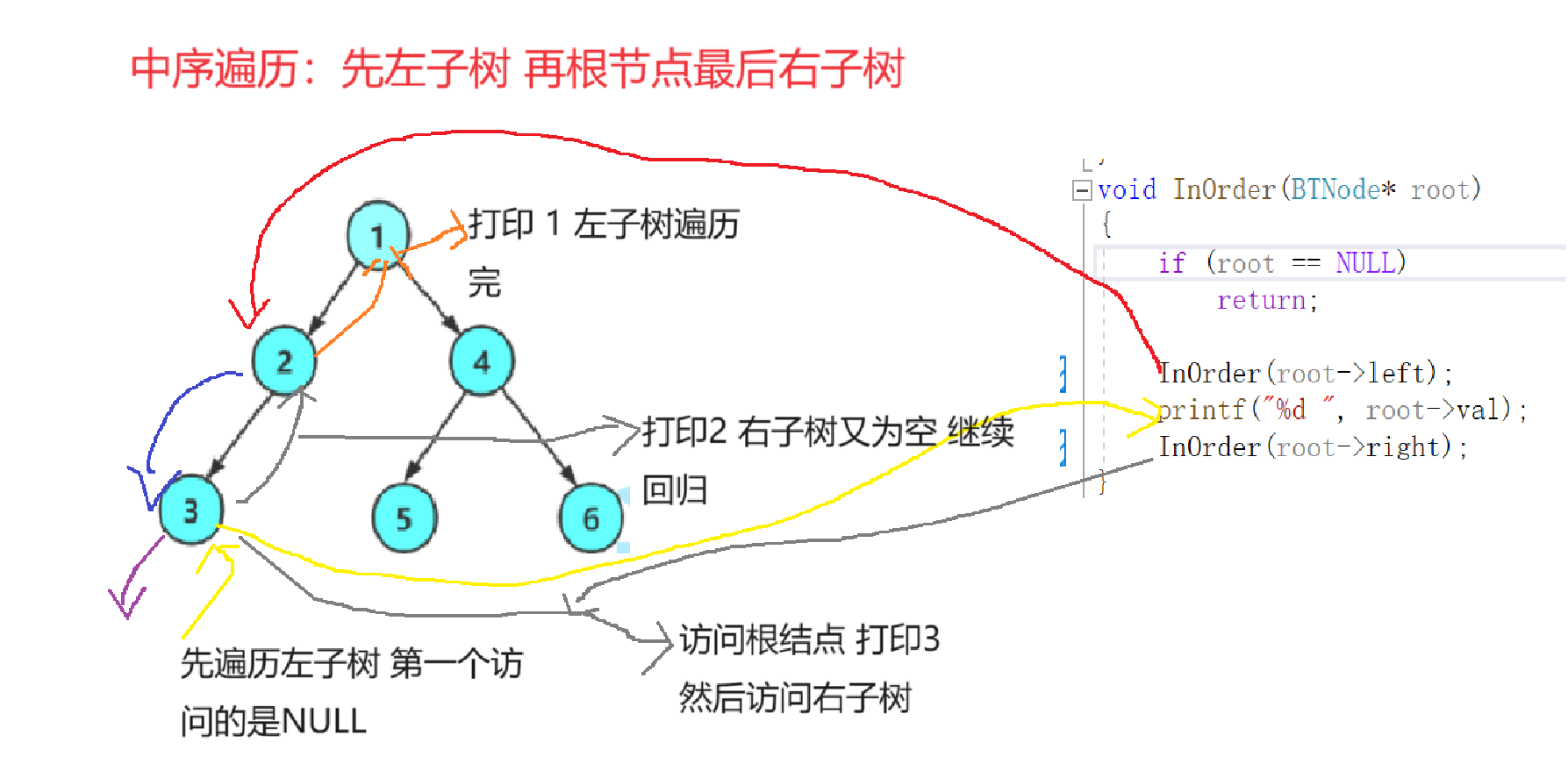
• 此时根结点的左子树遍历完 打印根结点1 开始遍历右子树
  
• 那照着这样的逻辑结果应该打印出 3 2 1 5 4 6
  
• 注意：这里很多人会有一个误区，如果有一个题问你，该二叉树第一个访问的是什么？
  中序遍历先遍历左子树，那么很多人都误以为先访问的是3，但其实访问的是NULL也就是3的左子树，然后才是根结点，最后是右子树也是NULL，此时该结点遍历完开始回归
  

3.后序遍历

• 后序遍历
• 同理，我们也可以相应的给后序遍历一个类似的解释
  当遍历时，先访问左子树再访问右子树最后访问根结点称为后序遍历

void PostOrder(BTNode* root)
{
    if (root == NULL)
        return;

    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->val);
}
1
2
3
4
5
6
7
8
9

• 上面已经画过两遍了，这里简单的画一下供大家参考
  
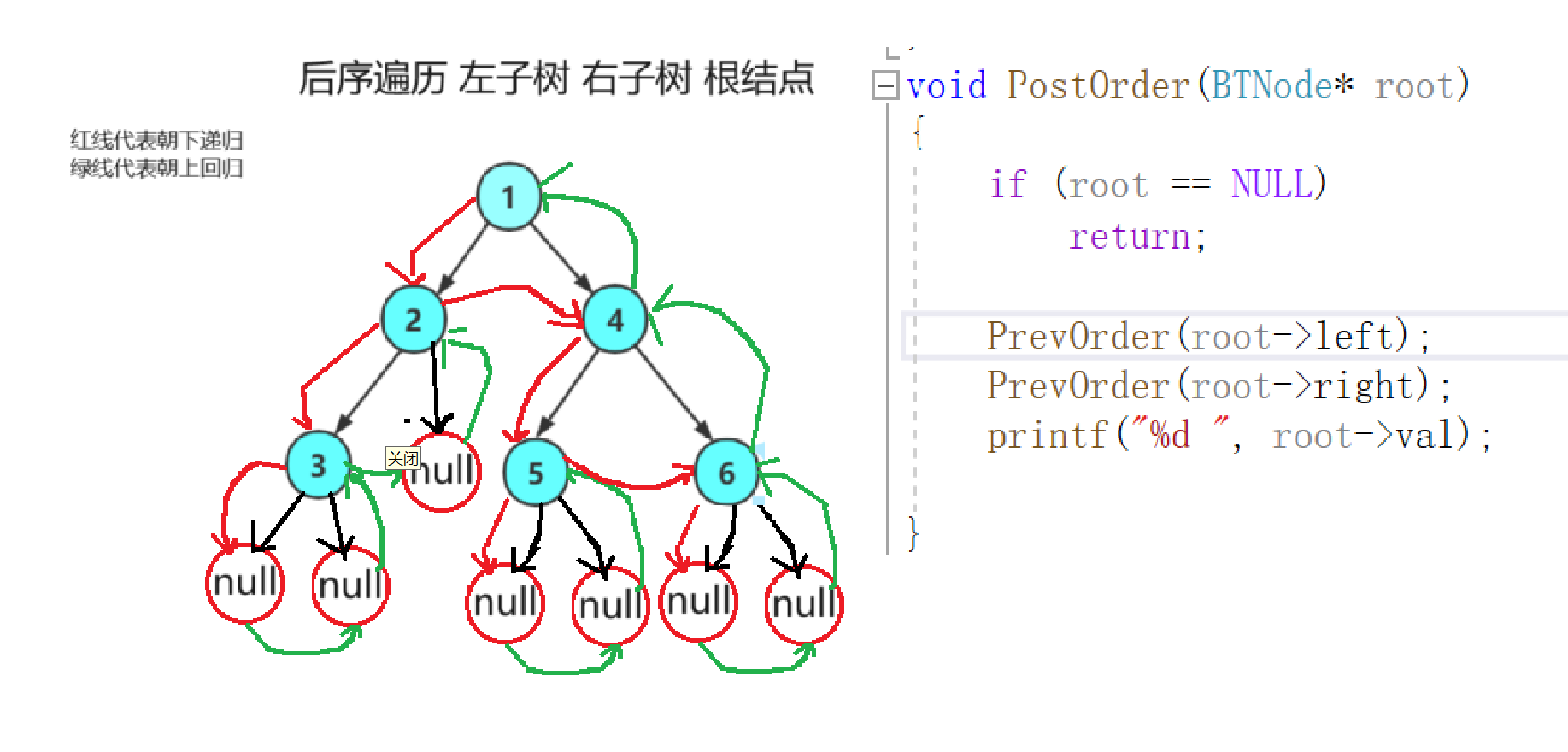
• 后序遍历结果应该是 3 2 5 6 4 1 我们来验证一下

---

三. 二叉树的层序遍历

• 与之前的几种遍历方法不同，层序遍历不需要使用递归，层序遍历的实现往往是伴随着队列的。
• 什么是层序遍历？
  就是一层一层的遍历二叉树
  
• 那我们怎末用队列实现呢？
• 我们知道，关于队列这个结构是先进先出的，也就是先放进去的一定是在队首，类似树中的根节点，利用这个特性，我们可以写出这段代码来实现层序遍历

void LevelOrder(BTNode* root)
{
	Que q;
	QueueInit(&q);//初始化队列

	if (root)
		QueuePush(&q, root);//把要遍历的二叉树的根节点插入队列中

	while (!QueueEmpty(&q))//队列判空
	{
		BTNode* front = QueueFront(&q);//获取队首元素
		printf("%d ", front->val);//打印队首存储的元素
		if (front->left)//队首的左子树不为空就把左子树插入队列
			QueuePush(&q, front->left);

		if (front->right)//队首的右子树不为空就把右子树插入队列
			QueuePush(&q, front->right);

		QueuePop(&q);//让队首离队
	}
	printf("\n");

	QueueDestroy(&q);//销毁队列
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

• 上面某些有关队列的操作看注释也没看懂的话可以看看这篇博客我对队列的介绍
  【数据结构】带你深入栈和队列，轻松实现各种接口功能
• 具体分为哪几步呢。我们来画图看看
  
  
  
  
  
  
• 相信此时你通过上图能明白层序遍历是怎么完成的，相比于之前的递归的前中后序遍历，层序遍历无疑简单了很多。

---

总结

• 今天的内容就到这里了，这些都是二叉树的基础的使用方法，但无疑是非常重要的，后面很多的难题以及其他用法都是从此繁衍而来，因此，弄懂这里非常重要
• 这里的难点是递归的理解，最好的理解方法就是像我一样画递归展开图，如果你能把递归的图给画明白，那我相信二叉树的遍历就对你不难了，好了，如果有任何有关的问题，欢迎在评论区提出或者直接私信我，我看到有时间会第一时间回复的！！

新人博主创作不易，如果感觉文章内容对你有所帮助的话不妨三连一下再走呗。你们的支持就是我更新的动力！！！

**（可莉请求你们三连支持一下博主！！！点击下方评论点赞收藏帮帮可莉吧）**