想要精通算法和SQL的成长之路 - 填充书架

前言

想要精通算法和SQL的成长之路 - 系列导航

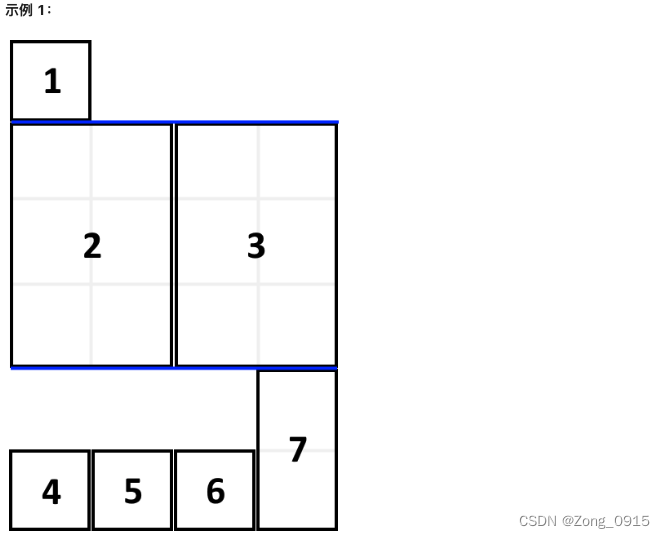
一. 填充书架

原题链接

题目中有一个值得注意的点就是：

• 需要按照书本顺序摆放。
• 每一层当中，只要厚度不够了，当前层最高的那一本书籍就视为本层的高度。

那么我们假设dp[i]： 代表从 book[0] 摆到 book[i] 的时书架的最小高度。

• 假设最后一层的第一本书的下标是 j，那么之前所有书本摆放的最小高度就是 dp[j-1]。
• 我们再计算出，下标在[j,i]（最后一层）的书本中，高度最高的那一本书（同时满足厚度不超过shelfWidth），高度为maxHeight。
• 那么当前的最小总高度是 res = Max(dp[i-1]+maxHeight，res)。即之前的总高度+最后一层的最高高度。

我们递归，从后往前递归。入参为遍历的书本下标。

1. 终止条件：下标 <0。代表没有书本了，停止递归。
2. 递归做的事情：循环[0,i]之间的所有元素，从后往前把书本放入最后一层，一旦厚度超出，终止遍历。否则，计算当前层的最高高度以及最小总高。

public class Test1105 {
    public int[][] books;
    public int shelfWidth;

    public int minHeightShelves(int[][] books, int shelfWidth) {
        this.books = books;
        this.shelfWidth = shelfWidth;
        return dfs(books.length - 1);
    }

    public int dfs(int i) {
        // 终止条件
        if (i < 0) {
            return 0;
        }
        int res = Integer.MAX_VALUE, maxHeight = 0, width = shelfWidth;
        for (int j = i; j >= 0; j--) {
            // 从后往前放书本
            width -= books[j][0];
            // 厚度不能超过 shelfWidth ，超过就代表放不下了
            if (width < 0) {
                break;
            }
            // 当前层最高高度
            maxHeight = Math.max(maxHeight, books[j][1]);
            // 更新总最低书架高度 = 上层最小总高度 + 当前层最高高度
            res = Math.min(res, dfs(j - 1) + maxHeight);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

这个解答其实对于用例比较多的情况，是会超时的。

1.1 优化

我们来看下上面代码的不好的点：

• 每次dfs的时候，循环的范围是：[0,j]。
• 循环内部又每次调用了dfs递归，即dfs[j-1]。

整个递归函数，只用到了一个索引的参数，我们可以发现，索引为1,2,3…的递归，被重复调用了非常多次。以当前索引为3为例：

• 第一次递归范围：[0,3]。
• 第二次递归范围：[0,2]。
• 第三次递归范围：[0,1]。
• …

那么我们可以用一个全局的变量去记录每次dfs返回的结果即可:

public class Test1105 {
    public int[][] books;
    public int shelfWidth;
    // 缓存dfs的结果
    public int[] dfsCache;

    public int minHeightShelves(int[][] books, int shelfWidth) {
        this.books = books;
        this.shelfWidth = shelfWidth;
        // 初始化
        dfsCache = new int[books.length];
        // 给个初始值，-1代表没有被执行过，即没有缓存
        Arrays.fill(dfsCache, -1);
        return dfs(books.length - 1);
    }

    public int dfs(int i) {
        // 终止条件
        if (i < 0) {
            return 0;
        }
        // 如果是-1，代表这层值没有执行过，往下走。否则，说明有缓存了，直接返回
        if (dfsCache[i] != -1) {
            return dfsCache[i];
        }
        int res = Integer.MAX_VALUE, maxHeight = 0, width = shelfWidth;
        for (int j = i; j >= 0; j--) {
            // 从后往前放书本
            width -= books[j][0];
            // 厚度不能超过 shelfWidth ，超过就代表放不下了
            if (width < 0) {
                break;
            }
            // 当前层最高高度
            maxHeight = Math.max(maxHeight, books[j][1]);
            // 更新总最低书架高度 = 上层最小总高度 + 当前层最高高度
            res = Math.min(res, dfs(j - 1) + maxHeight);
        }
        // 缓存下当前结果
        dfsCache[i] = res;
        return dfsCache[i];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43