• 第71步 时间序列建模实战：ARIMA建模（Python）

    基于WIN10的64位系统演示

    一、写在前面

    这一期，我们使用Python进行SARIMA模型的构建。

    同样，这里使用这个数据：

    《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndrome in Jiangsu Province, China》文章的公开数据做演示。数据为江苏省2004年1月至2012年12月肾综合症出血热月发病率。运用2004年1月至2011年12月的数据预测2012年12个月的发病率数据。

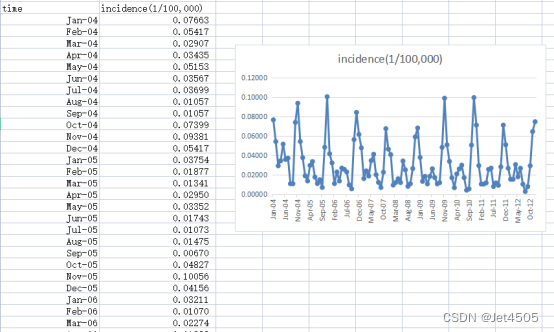
    终于到Pyhton，未来数期的模型构建，也都使用Python来搭建。

    而且我有一个大胆的想法，用GPT来直接跑代码。

    二、GPT建立SARIMA实战

    （1）咒语

    我有一批{原始数据}：江苏省2004年1月至2012年12月肾综合症出血热月发病率。运用2004年1月至2011年12月的数据构建SARIMA模型，模型参数可表示为SARIMA（p，d，q）（P，D，Q）s，使用模型预测2012年1月至12月的每个月的发病率数据。按照以下步骤进行：

    （1）构建一系列SARIMA模型，其中模型参数的取值范围为：p为0至3，d为0至1，q为0至3；P为0至3，D为0至1，Q为0至3；s为12；

    （2）从上面步骤构建的SARIMA模型中找出最优的模型，最优模型满足下面条件：（a）模型的AIC值、SBC值最小，R方最大；（b）模型的参数p、q、P和Q四个参数均具有统计学意义，P值小于0.05；

    （3）使用最优的模型分别预测“2004年1月至2011年12月的个月的发病率数据”以及“2012年1月至12月的每”，并打印出来，同时分别保存为csv文件。

    （4）最后只需要显示最优模型的模型参数（SARIMA（p，d，q）（P，D，Q）s）、模型的AIC值、SBC值、R方以及各个参数（p、q、P和Q）的统计学结果。

    原始数据见“{data.csv}”。

    你可以一步一步来，进行完一步操作以后，保存结果，然后问我是否继续分析。我说继续分析，你才继续。

    打开Code Interpreter，输入咒语，跟着GPT-4写代码：

    （a）让我们首先加载数据并查看前几行，以便了解数据的结构和内容。这样，

    1. # 导入必要的库
    2. import pandas as pd
    3. # 加载数据
    4. file_path = '/mnt/data/data.csv'
    5. data = pd.read_csv(file_path)
    6. # 显示前几行数据
    7. data.head()

    数据已成功加载，其中包括两列：

    time：时间，从2004年1月开始

    incidence：肾综合症出血热的月发病率

    （b）我们将首先绘制时间序列图来观察数据的趋势和季节性。然后，我们将进行平稳性检验以确定数据的性质。这些步骤有助于我们选择合适的SARIMA模型参数。

    1. # 导入绘图库
    2. import matplotlib.pyplot as plt
    3. # 绘制时间序列图
    4. plt.figure(figsize=(15, 6))
    5. plt.plot(data['incidence'], label='月发病率')
    6. plt.title('肾综合症出血热月发病率时间序列图')
    7. plt.xlabel('月份')
    8. plt.ylabel('发病率')
    9. plt.legend()
    10. plt.grid(True)
    11. plt.show()

    从时间序列图可以观察到，肾综合症出血热的月发病率似乎存在明显的季节性波动。下一步，我们将进行平稳性检验来确定时间序列的性质

    （c）我们将对该时间序列进行平稳性检验。平稳性是时间序列分析的重要前提，只有平稳的时间序列才能用于建立SARIMA模型。

    我们将使用ADF（Augmented Dickey-Fuller）检验来判断序列的平稳性。让我们开始吧。

    1. # 导入ADF检验函数
    2. from statsmodels.tsa.stattools import adfuller
    3. # 进行ADF检验
    4. result = adfuller(data['incidence'])
    5. adf_statistic, p_value, usedlag, nobs, critical_values, icbest = result
    6. # 输出ADF检验结果
    7. adf_result = {
    8.     "ADF统计量": adf_statistic,
    9.     "p值": p_value,
    10.     "滞后阶数": usedlag,
    11.     "观测值数量": nobs,
    12.     "临界值": critical_values,
    13.     "最大信息准则": icbest
    14. }
    15. adf_result

    ADF检验的结果如下：

    ADF统计量：-4.141

    p值：0.00083

    滞后阶数：11

    观测值数量：96

    临界值：

    1%：-3.500

    5%：-2.892

    10%：-2.583

    由于p值小于0.05，并且ADF统计量小于各个临界值，我们可以拒绝原假设，即序列存在单位根。因此，我们可以认为该时间序列是平稳的。

    接下来，我们将进行自相关（ACF）和偏自相关（PACF）图的绘制，以便选择合适的SARIMA模型参数。

    （d）接下来我们将绘制自相关函数（ACF）图和偏自相关函数（PACF）图。通过观察这些图形，我们可以初步确定SARIMA模型的非季节性参数p和q。

    1. # 导入ACF和PACF绘图函数
    2. from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
    3. # 绘制自相关函数（ACF）图
    4. plt.figure(figsize=(12, 6))
    5. plot_acf(data['incidence'], lags=40, title='自相关函数（ACF）图')
    6. plt.show()
    7. # 绘制偏自相关函数（PACF）图
    8. plt.figure(figsize=(12, 6))
    9. plot_pacf(data['incidence'], lags=40, title='偏自相关函数（PACF）图')
    10. plt.show()

    （e）下一步，我们将构建一系列SARIMA模型，并选择最优模型。模型参数的取值范围为：p 为0至3，d 为0至1，q 为0至3；P 为0至3，D 为0至1，Q 为0至3；s 为12。我们将基于AIC值、SBC值和模型参数的统计学意义来选择最优模型。这个过程可能需要一些时间，我们将尽快完成。让我们开始构建模型。

    （f）接下来我们将使用找到的最优SARIMA模型进行预测。

    首先，我们将预测2004年1月至2011年12月的每个月的发病率数据，并与实际数据进行比较。然后，我们将预测2012年1月至12月的每个月的发病率数据。

    让我们开始预测并将结果可视化。

    1. # 导入SARIMA模型
    2. from statsmodels.tsa.statespace.sarimax import SARIMAX
    3. # 分割数据为训练和测试集
    4. train_data = data['incidence'][:96]  # 2004年1月至2011年12月的数据用于训练
    5. test_data = data['incidence'][96:]   # 2012年1月至12月的数据用于测试
    6. # 设置参数范围
    7. p_values = range(0, 2)
    8. d_values = range(0, 1)
    9. q_values = range(0, 2)
    10. P_values = range(0, 2)
    11. D_values = range(0, 1)
    12. Q_values = range(0, 2)
    13. s_value = 12
    14. # 用于存储最优模型的信息
    15. best_model_info = {
    16.     "AIC": float('inf'),
    17.     "SBC": float('inf'),
    18.     "R_squared": float('-inf'),
    19.     "order": None,
    20.     "seasonal_order": None,
    21.     "model": None
    22. }
    23. # 遍历参数，寻找最优模型
    24. for p in p_values:
    25.     for d in d_values:
    26.         for q in q_values:
    27.             for P in P_values:
    28.                 for D in D_values:
    29.                     for Q in Q_values:
    30.                         try:
    31.                             # 构建SARIMA模型
    32.                             model = SARIMAX(train_data, order=(p, d, q), seasonal_order=(P, D, Q, s_value), enforce_invertibility=False)
    33.                             # 拟合模型
    34.                             model_fit = model.fit(disp=False)
    35.                             # 计算AIC和SBC
    36.                             AIC = model_fit.aic
    37.                             SBC = model_fit.bic
    38.                             # 检查p值
    39.                             p_values_summary = model_fit.pvalues
    40.                             if all(p_value < 0.05 for p_value in p_values_summary):
    41.                                 # 检查是否是最优模型
    42.                                 if AIC < best_model_info["AIC"] and SBC < best_model_info["SBC"]:
    43.                                     best_model_info["AIC"] = AIC
    44.                                     best_model_info["SBC"] = SBC
    45.                                     best_model_info["order"] = (p, d, q)
    46.                                     best_model_info["seasonal_order"] = (P, D, Q, s_value)
    47.                                     best_model_info["model"] = model_fit
    48.                         except:
    49.                             continue
    50.  
    51. # 打印最优模型信息
    52. best_model_info["order"], best_model_info["seasonal_order"], best_model_info["AIC"], best_model_info["SBC"]
    53. # 获取最优模型各个参数的p值
    54. p_values_of_best_model = best_model_info["model"].pvalues
    55.  
    56. # 打印各个参数的p值
    57. print("最优模型各个参数的p值：")
    58. for param, p_value in p_values_of_best_model.items():
    59.     print(f"{param}: {p_value}")

    输出结果：最优模型为SARIMA(1, 0, 0), (1, 0, 1) 12；AIC值为：-554.4732350048097，SBC值为-544.2158422389383。

    最优模型各个参数的p值：

    ar.L1: 4.4028848440349195e-11

    ar.S.L12: 0.0

    ma.S.L12: 5.4811119190045404e-09

    sigma2: 3.3027800780300363e-12

    （g）最后拟合和预测数据即可：

    1. # 使用最优模型进行全样本内预测（2004年1月至2011年12月）
    2. in_sample_forecast = best_model_info["model"].get_prediction(dynamic=False)
    3. in_sample_mean = in_sample_forecast.predicted_mean
    4. in_sample_conf_int = in_sample_forecast.conf_int()
    5. # 使用最优模型进行样本外预测（2012年1月至12月）
    6. out_sample_forecast = best_model_info["model"].get_forecast(steps=12)
    7. out_sample_mean = out_sample_forecast.predicted_mean
    8. out_sample_conf_int = out_sample_forecast.conf_int()
    9.  
    10. # 保存in_sample_conf_int的第二列为CSV文件
    11. in_sample_conf_int.iloc[:, 1].to_csv('in_sample_conf_int_second_column.csv', header=['incidence'])
    12. # 保存out_sample_conf_int的第二列为CSV文件
    13. out_sample_conf_int.iloc[:, 1].to_csv('out_sample_conf_int_second_column.csv', header=['incidence'])

    拟合和预测数据输出为CSV文件，自行取用作图即可。

    三、全部代码

    贴上所有代码：

    1. # 导入必要的库
    2. import pandas as pd
    3. # 加载数据
    4. file_path = 'data.csv'
    5. data = pd.read_csv(file_path)
    6. # 显示前几行数据
    7. data.head()
    8.  
    9. import matplotlib.pyplot as plt
    10. # 绘制时间序列图
    11. plt.figure(figsize=(15, 6))
    12. plt.plot(data['incidence'], label='月发病率')
    13. plt.title('肾综合症出血热月发病率时间序列图')
    14. plt.xlabel('月份')
    15. plt.ylabel('发病率')
    16. plt.legend()
    17. plt.grid(True)
    18. plt.show()
    19.  
    20. # 导入ADF检验函数
    21. from statsmodels.tsa.stattools import adfuller
    22. # 进行ADF检验
    23. result = adfuller(data['incidence'])
    24. adf_statistic, p_value, usedlag, nobs, critical_values, icbest = result
    25. # 输出ADF检验结果
    26. adf_result = {
    27.     "ADF统计量": adf_statistic,
    28.     "p值": p_value,
    29.     "滞后阶数": usedlag,
    30.     "观测值数量": nobs,
    31.     "临界值": critical_values,
    32.     "最大信息准则": icbest
    33. }
    34. adf_result
    35.  
    36. # 导入ACF和PACF绘图函数
    37. from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
    38.  
    39. # 绘制自相关函数（ACF）图
    40. plt.figure(figsize=(12, 6))
    41. plot_acf(data['incidence'], lags=40, title='自相关函数（ACF）图')
    42. plt.show()
    43. # 绘制偏自相关函数（PACF）图
    44. plt.figure(figsize=(12, 6))
    45. plot_pacf(data['incidence'], lags=40, title='偏自相关函数（PACF）图')
    46. plt.show()
    47.  
    48. # 导入SARIMA模型
    49. from statsmodels.tsa.statespace.sarimax import SARIMAX
    50. # 分割数据为训练和测试集
    51. train_data = data['incidence'][:96]  # 2004年1月至2011年12月的数据用于训练
    52. test_data = data['incidence'][96:]   # 2012年1月至12月的数据用于测试
    53. # 设置参数范围
    54. p_values = range(0, 2)
    55. d_values = range(0, 1)
    56. q_values = range(0, 2)
    57. P_values = range(0, 2)
    58. D_values = range(0, 1)
    59. Q_values = range(0, 2)
    60. s_value = 12
    61. # 用于存储最优模型的信息
    62. best_model_info = {
    63.     "AIC": float('inf'),
    64.     "SBC": float('inf'),
    65.     "R_squared": float('-inf'),
    66.     "order": None,
    67.     "seasonal_order": None,
    68.     "model": None
    69. }
    70. # 遍历参数，寻找最优模型
    71. for p in p_values:
    72.     for d in d_values:
    73.         for q in q_values:
    74.             for P in P_values:
    75.                 for D in D_values:
    76.                     for Q in Q_values:
    77.                         try:
    78.                             # 构建SARIMA模型
    79.                             model = SARIMAX(train_data, order=(p, d, q), seasonal_order=(P, D, Q, s_value), enforce_invertibility=False)
    80.                             # 拟合模型
    81.                             model_fit = model.fit(disp=False)
    82.                             # 计算AIC和SBC
    83.                             AIC = model_fit.aic
    84.                             SBC = model_fit.bic
    85.                             # 检查p值
    86.                             p_values_summary = model_fit.pvalues
    87.                             if all(p_value < 0.05 for p_value in p_values_summary):
    88.                                 # 检查是否是最优模型
    89.                                 if AIC < best_model_info["AIC"] and SBC < best_model_info["SBC"]:
    90.                                     best_model_info["AIC"] = AIC
    91.                                     best_model_info["SBC"] = SBC
    92.                                     best_model_info["order"] = (p, d, q)
    93.                                     best_model_info["seasonal_order"] = (P, D, Q, s_value)
    94.                                     best_model_info["model"] = model_fit
    95.                         except:
    96.                             continue
    97. # 打印最优模型信息
    98. best_model_info["order"], best_model_info["seasonal_order"], best_model_info["AIC"], best_model_info["SBC"]
    99. # 获取最优模型各个参数的p值
    100. p_values_of_best_model = best_model_info["model"].pvalues
    101. # 打印各个参数的p值
    102. print("最优模型各个参数的p值：")
    103. for param, p_value in p_values_of_best_model.items():
    104.     print(f"{param}: {p_value}")
    105.  
    106.  
    107. # 使用最优模型进行全样本内预测（2004年1月至2011年12月）
    108. in_sample_forecast = best_model_info["model"].get_prediction(dynamic=False)
    109. in_sample_mean = in_sample_forecast.predicted_mean
    110. in_sample_conf_int = in_sample_forecast.conf_int()
    111.  
    112. # 使用最优模型进行样本外预测（2012年1月至12月）
    113. out_sample_forecast = best_model_info["model"].get_forecast(steps=12)
    114. out_sample_mean = out_sample_forecast.predicted_mean
    115. out_sample_conf_int = out_sample_forecast.conf_int()
    116.  
    117. # 保存in_sample_conf_int的第二列为CSV文件
    118. in_sample_conf_int.iloc[:, 1].to_csv('in_sample_conf_int_second_column.csv', header=['incidence'])
    119.  
    120. # 保存out_sample_conf_int的第二列为CSV文件
    121. out_sample_conf_int.iloc[:, 1].to_csv('out_sample_conf_int_second_column.csv', header=['incidence'])

    收工！！！

    四、个人感悟

    Code Intrpreter还是强，不过就是分配的计算资源小了些，一旦需要计算比较大，就会卡死。所以我在咒语中加了这句：“你可以一步一步来，进行完一步操作以后，保存结果，e然后问我是否继续分析。我说继续分析，你才继续。”

    五、数据

    链接：https://pan.baidu.com/s/1EFaWfHoG14h15KCEhn1STg?pwd=q41n

    提取码：q41n

  • 相关阅读:
    Docker从认识到实践再到底层原理（二-2）｜Namespace+cgroups
    【3dmax】怎么将点删除而面保留
    mmdetection3d在win10下实现点云目标检测
    oradebug current_sql
    指针笔试题~走近大厂
    大数乘法算法
    webpack之Scope Hoisting（范围提升）
    【5 操作系统调度】
    SwiftUI 4.0 如何轻松在 iOS 16 中设置 TextEditor 背景色
    为什么要用vite,用vite的原因是什么
  • 原文地址：https://blog.csdn.net/qq_30452897/article/details/132916431