NO.396 旋转数组

题目

给定一个长度为 n 的整数数组 nums 。

假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组，我们定义 nums 的 旋转函数  F 为：

• F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]

返回 F(0), F(1), ..., F(n-1)中的最大值 。

生成的测试用例让答案符合 32 位 整数。

思路

思路1

双循环，根据对于索引进行 +1 计算，如果索引大于等于数组的总长，则减去数组的总长

缺点：由于是双重循环，因此时间复杂度为 

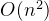
思路2

根据题目，列出F(0) 和F(1)的计算公式如下：

• F(0)=0×nums[0]+1×nums[1]+…+(n−1)×nums[n−1]
• F(1)=1×nums[0]+2×nums[1]+…+0×nums[n−1]

F(1) - F(0) = 1×nums[0]+1×nums[1]+…+1×nums[n−1] - n×nums[n−1]

从上图我们可以发现，1×nums[0]+1×nums[1]+…+1×nums[n−1]  相当于是nums数组的总和

因此我们可以设nums 的元素之和为 numSum。得到以下的公式：

当 1 ≤ k< n -1时

F(k)=F(k−1)+numSum−n×nums[n−k]

代码

class Solution {
    public int maxRotateFunction(int[] nums) {
        int f = 0, n = nums.length, numSum = Arrays.stream(nums).sum();
        for (int i = 0; i < n; i++) {
            f += i * nums[i];
        }
        int res = f;
        for (int i = n - 1; i > 0; i--) {
            f += numSum - n * nums[i];
            res = Math.max(res, f);
        }
        return res;
    }
}