LeetCode99之恢复二叉搜索树(相关话题：中序遍历)

目录

题目描述

解题思路

递归写法

非递归写法

思路拓展

难点剖析

树相关习题

---

题目描述

给你二叉搜索树的根节点 root ，该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

示例 1：

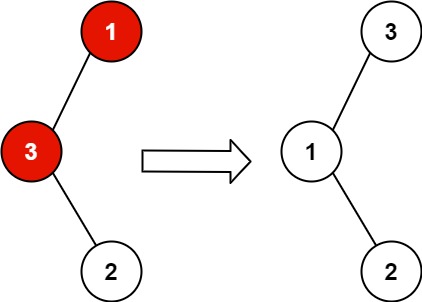
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：

• 树上节点的数目在范围 [2, 1000] 内
• -231 <= Node.val <= 231 - 1

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？

解题思路

常规的思路是中序遍历，检测出逆序节点就记录下来，那么如何检测逆序呢？

需要在每次递归中保存当前节点的前驱节点。

递归写法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
 
class Solution:
    def recoverTree(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        self.firstNode = None
        self.secondNode = None
        self.preNode = TreeNode(float("-inf"))
 
        def in_order(root):
            if not root:
                return
            in_order(root.left)
            if self.firstNode == None and self.preNode.val >= root.val:
                self.firstNode = self.preNode
            if self.firstNode and self.preNode.val >= root.val:
                self.secondNode = root
            self.preNode = root
            in_order(root.right)
 
        in_order(root)
        self.firstNode.val, self.secondNode.val = self.secondNode.val, self.firstNode.val

非递归写法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
 
class Solution:
    def recoverTree(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        firstNode = None
        secondNode = None
        pre = TreeNode(float("-inf"))
 
        stack = []
        p = root
        while p or stack:
            while p:
                stack.append(p)
                p = p.left
            p = stack.pop()
            
            if not firstNode and pre.val > p.val:
                    firstNode = pre
            if firstNode and pre.val > p.val:
                #print(firstNode.val,pre.val, p.val)
                secondNode = p
            pre = p
            p = p.right
        firstNode.val, secondNode.val = secondNode.val, firstNode.val

思路拓展

Morris中序遍历是一种二叉树的遍历算法，它的特点是不使用栈和递归，而且空间复杂度为O(1)。Morris遍历算法的核心思想是利用树的大量空闲指针（即空的右子节点），在遍历过程中修改树的结构，然后在遍历结束后再恢复树的结构。

Morris遍历的原理如下（只了解思想就可以，代码无需掌握）：

(1)如果当前节点的左子节点为空，那么直接输出当前节点的值，并将当前节点更新为其右子节点。

(2)如果当前节点的左子节点不为空，需要找到当前节点在中序遍历下的前驱节点。具体做法是：

   a) 遍历当前节点的左子树，找到最右侧的节点（即中序遍历下当前节点的前驱节点）。

   b) 如果前驱节点的右子节点为空，将它的右子节点设置为当前节点，然后将当前节点更新为其左子节点。

   c) 如果前驱节点的右子节点为当前节点，说明左子树已经遍历完，此时将前驱节点的右子节点重新设为空，输出当前节点的值，并将当前节点更新为其右子节点。

难点剖析

a) 遍历当前节点的左子树，找到最右侧的节点（即中序遍历下当前节点的前驱节点）。

b) 如果前驱节点的右子节点为空，将它的右子节点设置为当前节点，然后将当前节点更新为其左子节点。

这句话描述的是Morris遍历中处理当前节点左子节点不为空的情况。当当前节点的左子节点不为空时，我们需要找到当前节点在中序遍历下的前驱节点。如果前驱节点的右子节点为空，那么将前驱节点的右子节点设置为当前节点，这样在遍历完左子树后，可以通过前驱节点的右子节点返回到当前节点。然后将当前节点更新为其左子节点，继续遍历左子树。

举个例子，假设我们有如下二叉树：

```
    4
   / \
  2   6
 / \ / \
1  3 5  7
```

中序遍历的顺序是：1 2 3 4 5 6 7

对于根节点4，它的左子节点2不为空，所以我们需要找到4在中序遍历下的前驱节点，即节点3。此时，节点3的右子节点为空，我们将节点3的右子节点设置为节点4，并将当前节点更新为节点2，继续遍历左子树。这样，在遍历完左子树（1 2 3）后，可以通过节点3的右子节点返回到节点4，继续遍历右子树（5 6 7）。

c) 如果前驱节点的右子节点为当前节点，说明左子树已经遍历完如何理解

这句话描述的是在 Morris 遍历过程中，如果发现前驱节点的右子节点为当前节点，那么说明左子树已经遍历完。这是因为在之前的遍历过程中，我们会将前驱节点的右子节点设置为当前节点，以便在遍历完左子树后能够返回到当前节点。当我们再次访问到当前节点时，就说明左子树已经遍历完成，此时应该输出当前节点的值，并将当前节点更新为其右子节点，继续遍历右子树。

举个例子，还是使用上面的二叉树：

```
    4
   / \
  2   6
 / \ / \
1  3 5  7
```

中序遍历的顺序是：1 2 3 4 5 6 7

在之前的遍历过程中，我们将节点3的右子节点设置为节点4。当我们再次访问到节点4时，说明已经遍历完左子树（1 2 3），此时应该输出节点4的值，并将当前节点更新为其右子节点6，继续遍历右子树（5 6 7）。在输出当前节点的值之前，需要将前驱节点（节点3）的右子节点重新设为空，恢复树的原始结构。

树相关习题

LeetCode098之验证二叉搜索树（相关话题：二叉树中序遍历的应用）_在线验证二叉树遍历_数据与后端架构提升之路的博客-CSDN博客

LeetCode096不同的二叉搜索树(相关话题：卡特兰数)_数据与后端架构提升之路的博客-CSDN博客

LeetCode341之扁平化嵌套列表迭代器（相关话题：遍历N叉树，迭代器模式）_list.remove(0).getinteger()_数据与后端架构提升之路的博客-CSDN博客

LeetCode426之将二叉搜索树转化为排序的双向链表(相关话题：双向链表，二叉树中序)_将二进制搜索树转换为排序的循环双链表【问题描述】(利用链表二叉树)给定一个二进_数据与后端架构提升之路的博客-CSDN博客

LeetCode450之删除二叉搜索树中的节点(相关话题：二叉搜索树，删除)_数据与后端架构提升之路的博客-CSDN博客

剑指 Offer 26树的子结构(相关话题：对称性递归,在线算法)_数据与后端架构提升之路的博客-CSDN博客

LeetCode之团灭字典树相关题目_数据与后端架构提升之路的博客-CSDN博客