洛谷 Array 数论

题目：

对于长度为n的数组A，A中只包含从1到n的整数（可重复）。如果A单调不上升或单调不下降，A就可称为美丽的。 找出在长度为n时，有几个美丽的A。

---

思路：

这是一道数论题。

我们先找找“单调不递减的A”。

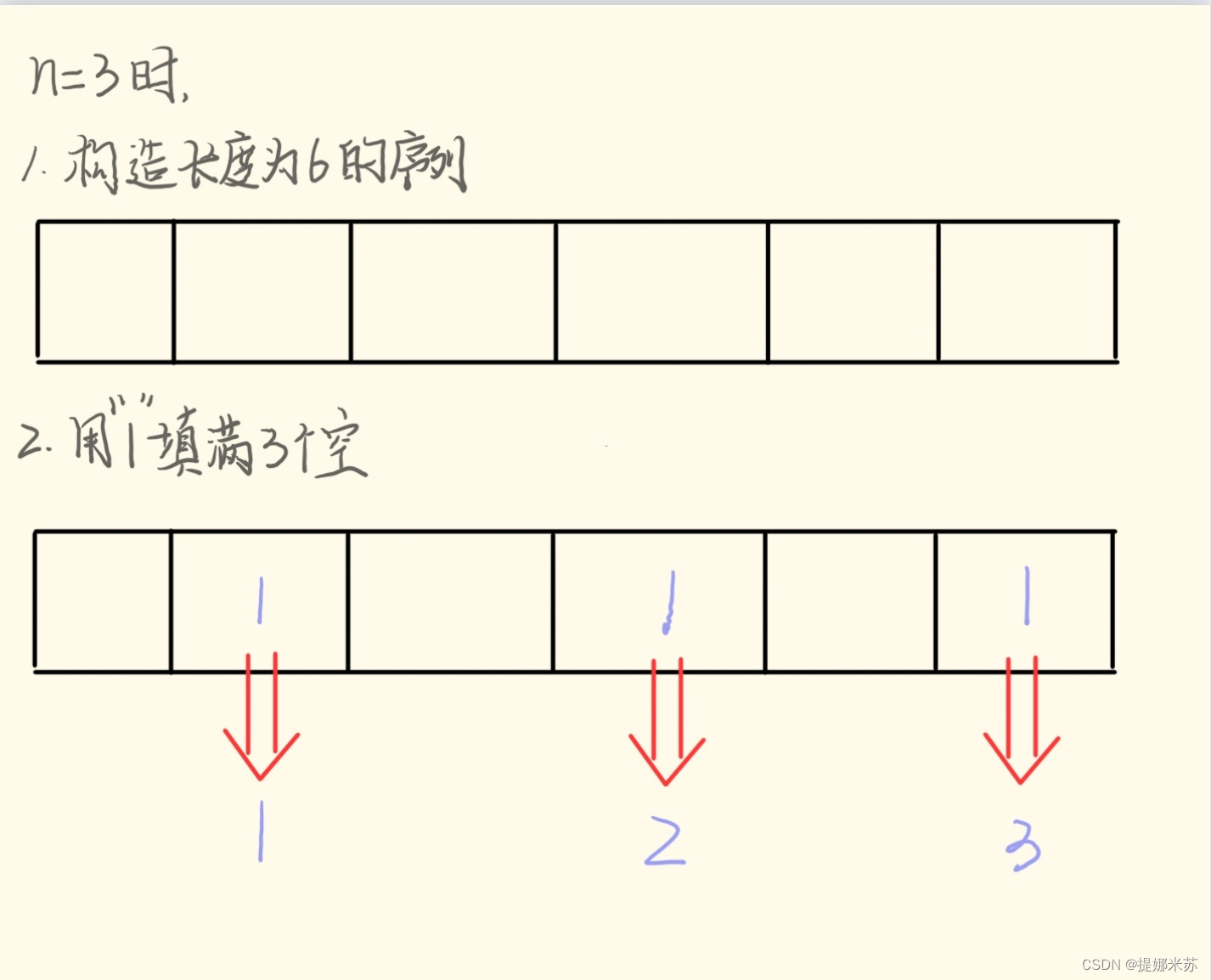
1.构造模型：设一个长度为（2*n-1）的序列，用1填满n个空，剩余（n-1）个空；

2.一一对应：找到每一个“1”，用其前方总共的“空格数”构成新序列。如下图所示。

 

 

3.合理性：构成的序列满足两个条件。

• （1）不递减：因为空格的数目只会累加。（如果两个“1”相邻的话会出现新序列中有相同数字的情况）
• （2）新序列中每个数字都是0到n-1的整数（可重复）对应题干中“从1到n的整数”:因为空格的数目最多只有n-1。

可见，单调不递减的A的数目=。

易得，单调不递增的A的数目=单调不递减的A的数目=。

所以，由容斥定理得，答案=不递增+不递减-既不递增.也不递减（常数序列）                                                                             .

---

代码展示：

#include<stdio.h>
#include<stdlib.h>
const int mod=1000000007;
long long ny(long long x)//逆元 取模 
{
	int cf=mod-2;long long base=x,ans=1;
	while(cf)
	{
		if(cf%2==1) ans*=base;
		ans%=mod;
		base=base*base;
		base%=mod;
		cf>>=1;
	}
	return ans;
}
long long c(int x,int y)//计算组合数 
{
	long long fz=1,fm=1,ans;int i;
	for(i=x;i>=x-y+1;i--) 
	{
		fz*=i;
		fz%=mod;
	}
	for(i=1;i<=y;i++)
	{
		fm*=i;
		fm%=mod;
	}
	fm=ny(fm);
	ans=fz*fm;
	ans%=mod;
	return ans;
}
long long zj;
int main()
{
	//答案是c(2n，n)-n 
    int n,i;
    scanf("%d",&n);
    zj=c(2*n,n);
    zj-=n;
    if(zj<0) zj+=mod;
	printf("%lld",zj);
	return 0;
}