【算法】堆排序 详解

排序： 排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中， r[i] = r[j]， 且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
（注意稳定排序可以实现为不稳定的形式， 而不稳定的排序实现不了稳定的形式）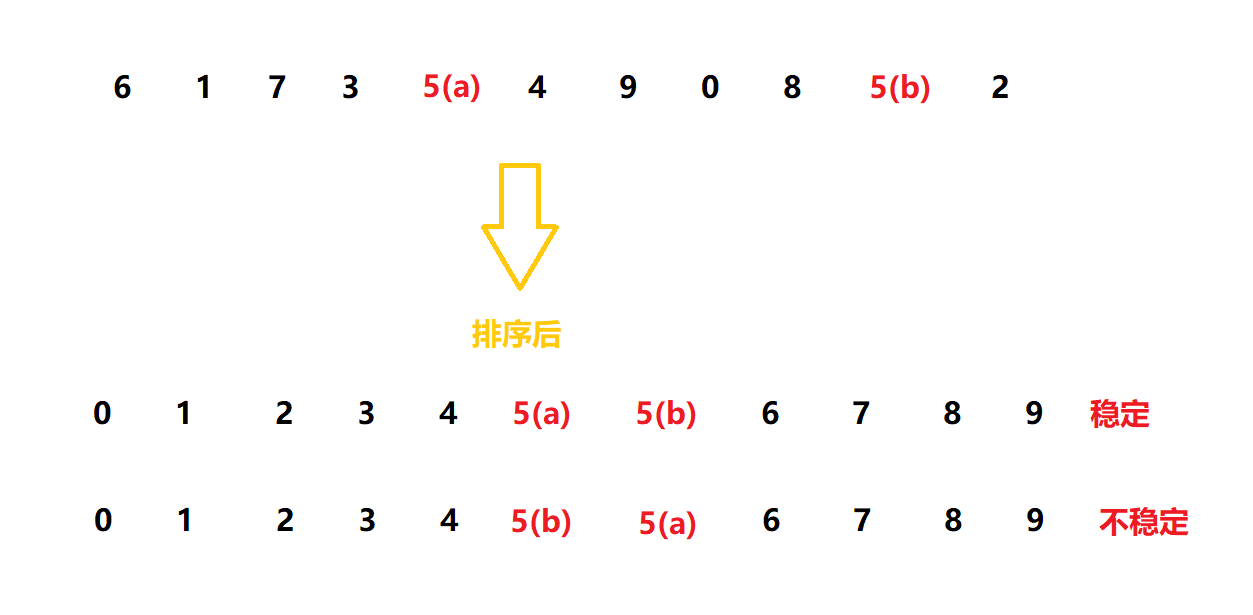

内部排序： 数据元素全部放在内存中的排序。

外部排序： 数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

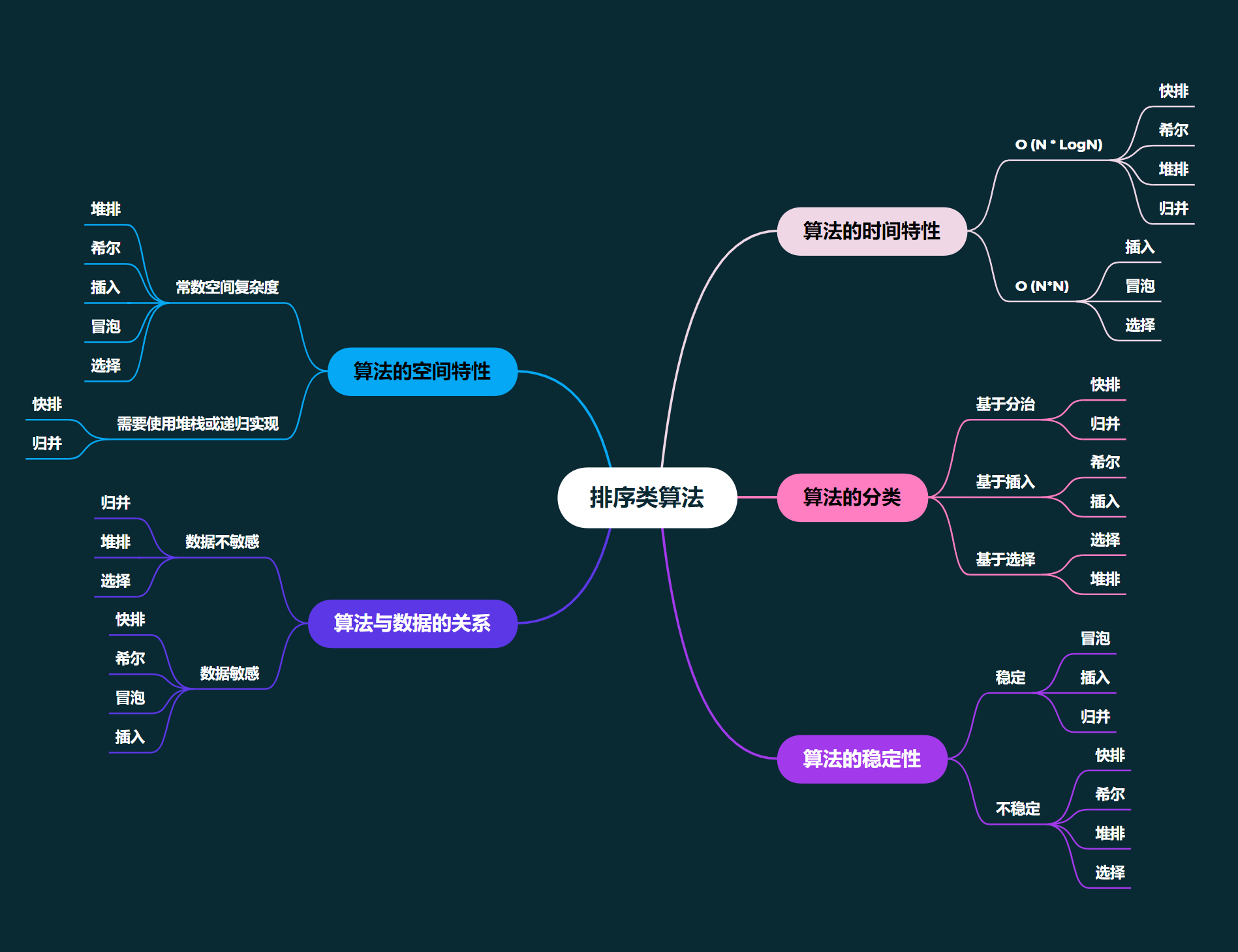
堆排序

堆排序 (Heapsort) 是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

为什么排升序建大堆?

• 因为假如排升序建小堆的话, 那么 我们只能得到最小的数字这一个, 同时堆的结构已经被破坏了, 因为我们直到最小值之后肯定要把这个最小值拿出来, 让剩下的元素进行排序, 也就是说堆的根节点下标要从 1 开始了, 这样就需要重新建堆了, 而建堆的时间复杂度是 O(N), 这样每选出来一个数, 就建一次堆, 总的时间复杂度就是 O(N*N) 了, 完全没有用上堆的优势。
• 但是假如排升序建大堆的话， 每次我们能选出来最大的值， 然后把它与最后位置的元素进行交换， 那么堆的根节点的位置还是从 0 开始，唯一可能不满足堆的性质情况就是 根节点小于 其他节点， 此时只需要 将根节点进行向下调整算法即可，不用重新建堆 。

友情链接：堆的讲解

基本思想: 建堆和排序。

• 建堆（Heapify）：

1. 首先，将待排序的数组视为一个完全二叉树。
2. 从数组的最后一个非叶子节点开始，逐个向前处理，对每个节点执行向下调整算法（将较大的元素交换到子节点的位置），直至整个数组构建成一个最大堆（Max Heap）或最小堆（Min Heap）。
3. 最大堆的特点是每个节点的值都大于或等于其子节点的值，最小堆则相反，每个节点的值都小于或等于其子节点的值。

• 排序：

1. 一旦构建好堆，堆顶元素就是最大（最小）元素。
2. 将堆顶元素与堆的最后一个元素交换位置，然后将堆的大小减 1。
3. 对新的堆顶元素执行一次下沉操作，将新的最大（最小）元素浮到堆顶。
4. 重复上述步骤，直到堆的大小为 1，排序完成。

堆排序的关键在于如何维护堆的性质，即使交换元素后，仍然保持堆的性质。这是通过向下调整操作来实现的，确保每次交换后最大（最小）元素移到堆的顶部。

代码实现

    public static void heapSort(int[] arr) {
        int len = arr.length;
        // 排升序
        // 建大堆
        // 从最后一个非叶子节点进行向下调整
        for (int i = (len-1-1)/2; i >= 0; i--) {
            shiftDown(arr, i, len);
        }
        // 排序
        // 从最后一个节点开始与第一个节点交换位置
        for (int i = len-1; i > 0; i--) {
            // 最大值放到最后面
            swap(arr, 0, i);
            // 交换完成后重新调整堆, 注意 此时堆的大小要 - 1, 但是 这正好与 i 相同, 所以直接使用了 i
            shiftDown(arr, 0, i);
        }
    }


    /**
     *  向下调整算法
     */
    public static void shiftDown(int[] arr, int index, int len) {
        int parent = index;
        int child = parent * 2 + 1;
        // 一直向下调整至符合堆 或者 至最后一个节点
        while (child < len) {
            if (child+1 < len && arr[child+1] > arr[child]) {
                child++;
            }
            if (arr[child] > arr[parent]) {
                // 交换节点
                swap(arr, parent, child);
                // 继续向下调整
                parent = child;
                child = parent * 2 + 1;
            } else {
                // 调整完成
                break;
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

总结：

• 时间复杂度： O（N*logN）
• 空间复杂度： O（1）
• 是不稳定排序: 向下调整过程中, 可能相对顺序发生变化
• 对数据不敏感: 不管原本数据怎么分布, 都要先建堆, 然后排序
• 相对于快速排序和归并排序，堆排序通常效率较低，因为它的数据访问模式不够连续，可能导致缓存不命中

以上就是对堆排序的讲解， 希望能帮到你 ！
评论区欢迎指正 ！