线性空间、子空间、基、基坐标、过渡矩阵

线性空间的定义

        满足加法和数乘封闭。也就是该空间的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里。进一步可以理解为该空间中的所有向量满足加法和数乘的组合封闭。即若 V 是一个线性空间，则首先需满足：

注：线性空间里面的元素称为向量 

线性空间证明

• 若要证明 V 是数域 P 上的线性空间（表示为V(P))，必须验证 V 对于向量的加法与数乘运算封闭，且满足8条性质；
• 若要说明 V 不是数域 P上的线性空间，则只需说明 V 对于向量的加法与数乘运算其中之一不封闭，或者运算不满足8条中的某一条即可。

例题：

证明：定理1.1 线性空间Ｖ 有唯一的零元素，任一元素也有唯一的负元素.
注：零元素不一定都是0.

 

常见的线性空间

比如 就是一个线性空间，图形表示就是一个平面直角坐标系。任取向量  和 做线性组合，+=

{0} （向量0）也是一个线性空间，并且是最简单的线性空间，很容易验证0满足加法数乘封闭和8条运算规则虽然很容易就列出了两个线性空间，但并不是所有空间都是线性空间.

非线性空间

线性子空间

定义：设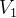是数域 K 上的线性空间Ｖ的一 个非空子集合，且对已有的线性运算满足 ：
（１）如果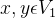，则。
（２）如果，则 。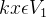
注：(1)(2)表示的是加法和数乘封闭原则。
则称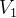为Ｖ的线性子空间或子空间。     
如果 (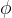表示空集) 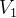，称为平凡子空间；否则称为非平凡子空间。

例如：

基

 

例题：

在中，求 在基（I）：

下的坐标。

由：

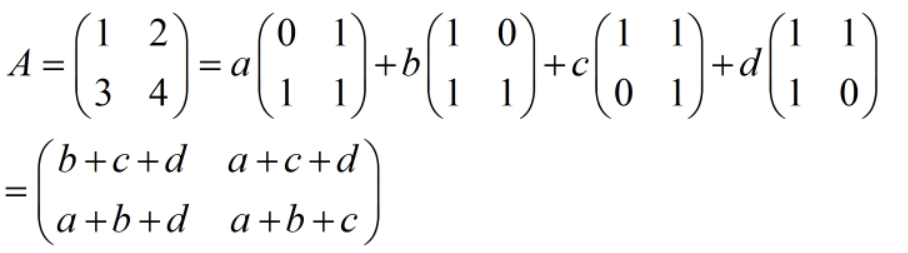
 解出：

从而A在基（I）下的坐标为：

基变换与坐标变换

 

坐标变换公式为式1.1.8 

 例题：