学不会的线段树

前言（胡言乱语）

“杭电杯”被狠狠薄纱😭😭😭，发现队友都是大佬，只有我是蒟蒻！！！具体表现为(包括但不限于)只有我还不会线段树😭，狠狠泪目！这就学🥀(･_･;

线段树的概念

线段树（Segment Tree）是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

线段树的应用

线段树适合解决的问题的特征是：大区间的解可以从小区间的解合并而来（区间加法!），即对于一个[L,R] = [L,M] + [M + 1,R].线段树对于区间的修改、维护和查询的时间复杂度优化为log级别。如果是要修改一个元素（单点修改），直接修改叶子节点上元素的值，然后从从下往上更新线段树；如果修改的是一个区间的元素（区间修改），需要用到Lazy-Tag技术。

线段树的构造

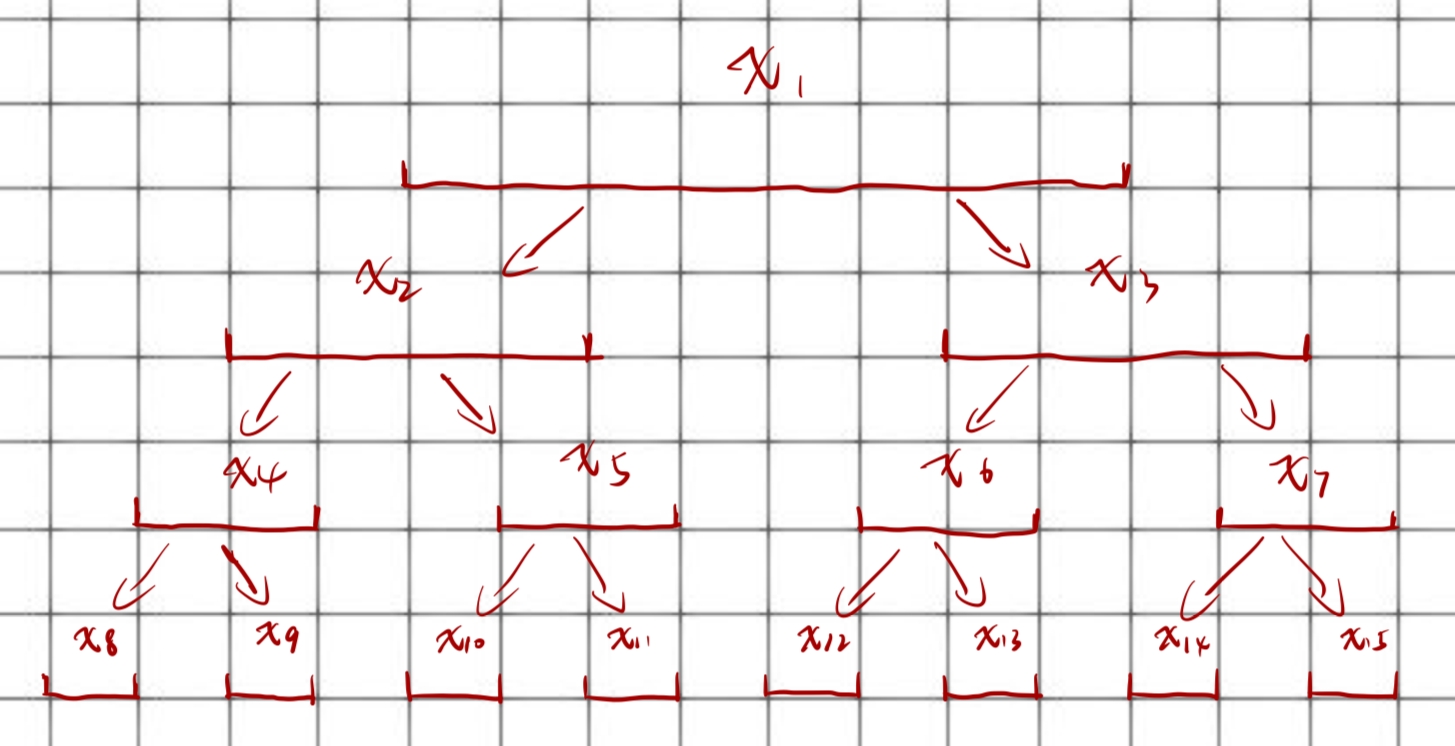
节点的构造

我们一般采用静态数组实现满二叉树，父节点和子节点之间的访问非常简单，缺点是最后一行有大量节点被浪费。

//定义二叉树数据结构
struct {
    int L;//左儿子
    int R;//右儿子
    int data;//记录线段i的最值或区间和
}tree[N * 4];
 
//直接用数组表示二叉树
int tree[N * 4];//记录线段i的最值或区间和

这两种都满足index_l = index_p << 1，index_r = index_p << 1 | 1

注意：二叉树的空间需要开N * 4，即元素数量的4倍

建树

建树的过程就是利用递归的思想，从上往下建树，从下往上传递区间值

int ls(int p){
    return p << 1;
}
 
int rs(int p){
    return p << 1 | 1;
}
 
void push_up(int p){
    tree[p] = tree[ls(p)] + tree[rs(p)];
}
 
void build(int p,int pl,int pr){
    if(pl == pr){
        tree[p] = a[pl];//给叶节点赋值
        return ;
    }
    int mid = (pl + pr) >> 1;//折半
    build(ls(p),pl,mid);//构造左子树
    build(rs(p),mid + 1,pl);//构造右子树
    push_up(p);//更新节点信息
}

区间查询

查询区间最值

以上面这个图为例，我们现在查询区间[3，7]之间的最值，从根节点开始，查询左右子树，存在一下3种情况
1、如果要查询的区间完全覆盖查询区间，就可以直接取值
2、如果要查询的区间与查询区间有交集，继续向下查询
3、如果要查询的区间与查询区间没有交集，那这个节点以及所有子节点的值对结果没有贡献

查询区间和

以上面这个图为例，我们现在查询区间[3，7]之间的和，从根节点开始，查询左右子树，存在一下3种情况
1、如果要查询的区间完全覆盖查询区间，就可以直接取值
2、如果要查询的区间与查询区间有交集，继续向下查询
3、如果要查询的区间与查询区间没有交集，那这个节点以及所有子节点的值对结果没有贡献

不难发现，无论要查询的是什么基本的思路都是：根据区间直接的覆盖情况来决定取值还是继续递归。

区间查询代码

int query(int l,int r,int p,int pl,int pr){//区间查询
    if(l <= pl && pr <= r){//完全覆盖
        return tree[p];//根据需要返回相应的值
    }
    int mid = (pl + pr) >> 1;
    if(l <= mid){//左子树上有交集
        res += query(l,r,pl, ls(p),mid);
    }
    if(r > mid){//右子树上有交集
        res += query(l,r,pr,mid + 1,rs(p));
    }
    return res;
}

区间操作与Lazy-Tag

Lazy-Tag

利用线段树的特征：线段树的节点tree[i]记录了区间i的值。可以再定义一个tag[i]用它统一记录区间i的修改，而不是一个一个地修改区间内的每个元素。看起来就慢的嘞
懒标记的精髓是：打标记和下传操作。若修改的是一个线段区间，就只对这个区间进行整体上的修改，打上tag标记，而它的子树先不进行修改，等需要使用到它的子树的时候，再对它的子树进行修改，把标记下传。

区间修改

以上图为例，我们现在要把区间[4,7]内的每个元素加2，按以下步骤进行操作：
1、左子树递归到节点11（标红的点），[4,4]被完全覆盖，打上标记tag[11] = 2，更新节点的值，不再继续深入
2、左子树递归返回，更新父节点的值

3、右子树递归到节点6，[5,6]被完全覆盖，打上标记tag[6] = 2，更新节点的值，不再继续深入
4、右子树递归返回，更新父节点的值

5、右子树递归到节点14，[7,7]被完全覆盖，打上标记tag[14] = 2，更新节点的值，不再继续深入
6、右子树递归返回，更新父节点的值

Q：好像tag并没有什么用啊
A：因为我们这里只对某个区间进行了一次操作，如果对多个区间进行多次操作的话，tag的作用就能很好的体现出来了

区间修改代码

void addTag(int t,int p,int pl,int pr){
    tag[p] += t;//给节点p打标记
    tree[p] += t * (pr - pl + 1);//更新节点信息
}
 
void push_down(int p, int pl, int pr){
    if(tag[p]){//如果有标记，把标记下传
        int mid = (pl + pr) >> 1;
        addTag(tag[p],ls(p),pl,mid);
        addTag(tag[p],rs(p),mid + 1,pr);
        tag[p] = 0;//自己的标记被传走
    }
}
 
void update(int l,int r,int p,int pl,int pr,int t){
    if(l <= pl && pr <= r){//完全覆盖
        addTag(t,p,pl,pr);//给节点p打标记
        return ;
    }
    push_down(p,pl,pr);
    int mid = (pl + pr) >> 1;
    update(l,r,ls(p),pl,mid,t);
    update(l,r,rs(p),mid + 1,pr,t);
    push_up(p);//更新节点信息
}

一点练习

这里码一点传送门

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $k$。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 $[x,y]$ 内每个数加上 $k$。
2. 2 x y：输出区间 $[x,y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

样例输出 #1

11
8
20

提示

对于 $30\mathrm{\%}$ 的数据：$n\le 8$，$m\le 10$。
对于 $70\mathrm{\%}$ 的数据：$n\le {10}^3$，$m\le {10}^4$。
对于 $100\mathrm{\%}$ 的数据：$1\le n,m\le {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。

【样例解释】

点击查看蒟蒻代码

#include 
#define int long long
const int N = 1e5 + 5;
//直接用数组表示二叉树
int tree[N * 4];//记录线段i的最值或区间和
int tag[N * 4];//lazy标记
int a[N];
int ls(int p){
    return p<<1;
}
 
int rs(int p){
    return p<<1|1;
}
 
void push_up(int p){
    tree[p] = tree[ls(p)] + tree[rs(p)];
}
 
void build(int p,int pl,int pr){//p为节点编号指向[pl,pr]
    if(pl == pr){
        tree[p] = a[pl];//给叶节点赋值
        return ;
    }
    int mid = (pl + pr)>>1;//折半
    build(ls(p),pl,mid);//构造左子树
    build(rs(p),mid + 1,pr);//构造右子树
    push_up(p);//更新节点信息
}
 
void addTag(int t,int p,int pl,int pr){
    tag[p] += t;//给节点p打标记
    tree[p] += t * (pr - pl + 1);//更新节点信息
}
 
void push_down(int p, int pl, int pr){
    if(tag[p]){//如果有标记，把标记下传
        int mid = (pl + pr)>>1;
        addTag(tag[p],ls(p),pl,mid);
        addTag(tag[p],rs(p),mid + 1,pr);
        tag[p] = 0;//自己的标记被传走
    }
}
 
void update(int l,int r,int p,int pl,int pr,int t){
    if(l <= pl && pr <= r){//完全覆盖
        addTag(t,p,pl,pr);//给节点p打标记
        return ;
    }
    push_down(p,pl,pr);
    int mid = (pl + pr)>>1;
    if(l <= mid) update(l,r,ls(p),pl,mid,t);
    if(r > mid) update(l,r,rs(p),mid + 1,pr,t);
    push_up(p);//更新节点信息
}
 
int query(int l,int r,int p,int pl,int pr){//区间查询
    if(l <= pl && pr <= r){//完全覆盖
        return tree[p];//根据需要返回相应的值
    }
    push_down(p,pl,pr);//递归子树
    int mid = (pl + pr)>>1;
    int res = 0;
    if(l <= mid){//左子树上有交集
        res += query(l,r,ls(p), pl,mid);
    }
    if(r > mid){//右子树上有交集
        res += query(l,r,rs(p),mid + 1,pr);
    }
    return res;
}
 
signed main(){
    std::ios::sync_with_stdio(0);
    std::cin.tie(0);std::cout.tie(0);
    int n,m;
    std::cin>>n>>m;
    for(int i = 1;i <= n;i ++){
        std::cin>>a[i];
    }
    build(1,1,n);
    while (m --){
        int op;
        std::cin>>op;
        if(op == 1){
            int x,y,k;
            std::cin>>x>>y>>k;
            update(x,y,1,1,n,k);
        }else if(op == 2){
            int x,y;
            std::cin>>x>>y;
            std::cout<<query(x,y,1,1,n)<<"\n";
        }
    }
    return 0;
}
 

后记

如果有任何问题，欢迎随时指正，感激不尽🌹🌹🌹
ps：换了电脑🌹都没之前的生动了/(ㄒoㄒ)/~~