C++算法之旅、04 基础篇 | 第一章基础算法

常用代码模板1——基础算法 - AcWing

ios::sync_with_stdio(false)

提高 cin 读取速度，副作用是不能使用 scanf

数据输入规模大于一百万建议用scanf

快速排序

基于分治 nlog(n) (期望值)

确定分界点

q[L]、q[ (L+R) / 2 ]、q[R]、随机点
调整区间 最难部分

所有 <=x的元素在x左半边，所有> = x 的元素在 x 右半边

暴力做法： 开两个数组 a, b，遍历 q，如果 <=x的元素放a，> x 的元素放 b。把 a、b 的元素分别放入 q 里面去，q 相当于 a + x + b 。扫了两遍 O(n)
优美方法： 开两个指针 a, b, 同时往中间走，a 先走，直到元素 >= x，i 停下来。移动 j，直到元素 < x，此时两个指针对应元素互换，各自移动一位
递归处理左右两段

785 ⭐

785. 快速排序 - AcWing题库

读入大量数据时，scanf更快一些。

另外本题有特殊情况，该情况下每次取区间起点或者终点作为分界点，则会超时。分界点换成随机值，或者区间中点即可。

highlighter- perl

#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int n;
int q[N];

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j) {
        do i++;
        while (q[i] < x);
        do j--;
        while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
    // ^ 在[1,2]数组情况下x不能取右边界点，否则会陷入死循环
    // quick_sort(q, l, i-1), quick_sort(q, i, r);
    // ^ 在[1,2]数组情况下x不能取左边界点，否则会陷入死循环
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);
    quick_sort(q, 0, n - 1);
    for (int i = 0; i < n; i++) printf("%d ", q[i]);

    return 0;
}

786

786. 第k个数 - AcWing题库

highlighter- perl

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;
int q[N];

void quick_sort(int q[], int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while (i < j) {
        do i++;
        while (q[i] < x);
        do j--;
        while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main() {
    int n, k;
    cin >> n >> k;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    quick_sort(q, 0, n - 1);
    printf("%d", q[k - 1]);

    return 0;
}

归并排序

基于分治 nlog(n)

找分界点，mid = (l+r) / 2（归并是找下标，快排是找数）
递归排序left，right
归并，把两个有序数组合二为一，使用双指针法。O(n)，需要额外辅助数组

排序算法的稳定与否，就是排序过程中数组中两个相等的数据，经过排序后，排序算法能保证其相对位置不发生变化，是稳定排序算法。归并过程中发现两个相同元素优先放入第一个指针的元素

787 ⭐

787. 归并排序 - AcWing题库

highlighter- perl

#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r) {
    if (l >= r) return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else
            tmp[k++] = q[j++];
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for (int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    merge_sort(q, 0, n - 1);
    for (int i = 0; i < n; i++) {
        printf("%d ", q[i]);
    }
    return 0;
}

788 ⭐⭐

788. 逆序对的数量 - AcWing题库

还要考虑逆序对数量，最大数 n * (n - 1) / 2 = 5 * 1e9 大于 INT_MAX，需要用 long long

highlighter- perl

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int n;
int q[N], tmp[N];

LL merge_sort_count(int q[], int l, int r) {
    if (l >= r) return 0;
    int mid = l + r >> 1;
    int k = 0, i = l, j = mid + 1;
    LL count = merge_sort_count(q, l, mid) + merge_sort_count(q, mid + 1, r);
    while (i <= mid && j <= r) {
        if (q[i] <= q[j])
            tmp[k++] = q[i++];
        else {
            count += mid - i + 1;
            tmp[k++] = q[j++];
        }
    }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];
    for (int i = l, k = 0; i <= r; i++, k++) q[i] = tmp[k];
    return count;
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }

    cout << merge_sort_count(q, 0, n - 1);

    return 0;
}

整数二分

整数二分的本质并不是单调性。本质是将区间一分为二，寻找边界点（左区间边界还是右区间边界）。

每次缩短区间一半，答案依旧在缩短的区间内，直到区间长度为1，此时就是边界点。

二分一定是有解的，此时 l==r，根据二分出来的边界点判断题目有没有解

左区间边界点

取中点mid = l+r+1 >> 1，判断该点是否符合左区间性质
- 如果成立说明mid在左区间，边界点在 [mid,r]，此时 l = mid
- 不成立说明mid不在左区间，边界点在 [l,mid-1]，此时 r = mid-1

右区间边界点

取中点mid = l+r >> 1，判断该点是否符合右区间性质
- 如果成立说明mid在右区间，边界点在 [l,mid]，此时 r = mid
- 不成立说明mid不在左区间，边界点在 [mid+1,r]，此时 l = mid+1

mid分子加1

性质成立条件中：l = mid ，加1；r = mid ，不加1

不加 1，当 l = r - 1 时，由于向下取整，mid = l，当性质条件成立， l = mid = l 死循环。加1后，mid = r，不会死循环。

789 ⭐

789. 数的范围 - AcWing题库

左区间边界点与右区间边界点都涉及

highlighter- perl

#include 
#include 

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int q[N];

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%d", &q[i]);
    }
    while (m--) {
        int k;
        cin >> k;
        // ^ 寻找右区间边界点
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (q[mid] >= k)
                r = mid;
            else
                l = mid + 1;
        }
        if (q[l] != k) {
            cout << "-1 -1" << endl;
            continue;
        } else
            cout << l << " ";
        l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (q[mid] <= k)
                l = mid;
            else
                r = mid - 1;
        }
        cout << r << endl;
    }
    return 0;
}

浮点数二分

浮点数没有整除向下取整，可以精准一分为二，不需要处理边界。处理精度问题，加上经验值2，多处理两位小数。

highlighter- excel

// while(r-l >= 1e-8)
for (int i = 0; i < 100; i++) {
    double mid = (l + r) / 2;
    if (mid * mid * mid >= x)
        r = mid;
    else
        l = mid;
}

790 ⭐

790. 数的三次方根 - AcWing题库

highlighter- cpp

#include 
#include 

using namespace std;

int main() {
    double x;
    cin >> x;
    double l = 0, r = x;
    if (x < -1)  // 负数时调换两者位置
        l = x, r = 0;
    else if (x > -1 && x < 1)  // 小数时范围是 [-1,1]
        l = -1, r = 1;

    // while(r-l >= 1e-8)
    for (int i = 0; i < 100; i++) { // 区间长度 / (1 << 100) 
        double mid = (l + r) / 2;
        if (mid * mid * mid >= x)
            r = mid;
        else
            l = mid;
    }
    printf("%lf\n", l);
    return 0;
}

ANTI WEB SPIDER BOT www.cnblogs.com/linxiaoxu

高精度（整数运算）

大整数位数 1e6 ，小整数值 <= 1e9 。（python、java自带大整数类型）

A + B

791. 高精度加法 - AcWing题库

highlighter- arduino

#include 
#include 
#include 

using namespace std;

// 加引用符不用拷贝一遍效率更高
vector<int> add(vector<int>& A, vector<int>& B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(1);
    return C;
}

int main() {
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    auto C = add(A, B);
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}

A - B

792. 高精度减法 - AcWing题库

要保证 A >= B，如果B大，则算 -(B - A) ；如果 A、B 有负数，可以转换成 |A| - |B| 或 |A| + |B|。

highlighter- arduino

#include 
#include 
#include 

using namespace std;

// 加引用符不用拷贝一遍效率更高
vector<int> sub(vector<int>& A, vector<int>& B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t = A[i] - t;
        // 判断越界
        if (i < B.size()) t -= B[i];
        // ^ 两种情况合二为一
        C.push_back((t + 10) % 10);
        t = t < 0 ? 1 : 0;
    }
    // ^ 去掉前导0
    while (C.size() > 1 && C.back() == 0) {
        C.pop_back();
    }
    return C;
}

// 判断 A>=B
bool cmp(vector<int>& A, vector<int>& B) {
    if (A.size() > B.size())
        return true;
    else if (A.size() < B.size())
        return false;
    else
        for (int i = A.size() - 1; i >= 0; i--) {
            if (A[i] != B[i]) return A[i] > B[i];
        }
    return true;
}

int main() {
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    if (cmp(A, B)) {
        auto C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    } else {
        auto C = sub(B, A);
        cout << '-';
        for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    }
    return 0;
}

A * b

793. 高精度乘法 - AcWing题库

把 b 看成一个整体去和 A 一位一位乘；记得处理b为0时的特殊情况、还有高位进位

highlighter- arduino

#include 
#include 
#include 

using namespace std;

vector<int> mul(vector<int> A, int b) {
    if (b == 0) return vector<int>{0};
    vector<int> C;
    int t = 0; // 进位
    for (int i = 0; i < A.size() || t; i++) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) {
        A.push_back(a[i] - '0');
    }

    auto C = mul(A, b);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    return 0;
}

A / b

794. 高精度除法 - AcWing题库

highlighter- arduino

#include 
#include 
#include 
#include 

using namespace std;

// A / b 商 C 余 r
vector<int> div(vector<int> A, int b, int& r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) {
        A.push_back(a[i] - '0');
    }
    int r;
    auto C = div(A, b, r);
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    cout << endl << r << endl;
    return 0;
}

一维前缀和

前缀和、差分是一对逆运算。前缀和下标从 1 开始， $S i = a_{1} + a_{2} + . . . + a_{i}$ ， $S_{0} = 0$

$S [i] = S [i - 1] + a_{i}$ ，预处理 O(n)

重要应用

算 [L,R] 区间内元素和，循环遍历需要 O(n) 复杂度。而使用前缀和 $S_{r} - S_{l - 1}$ 复杂度为 O(1)

下标从1开始

下标从1开始方便处理边界，求 [1,10] 等于 $S_{10} - S_{0}$

若下标从0开始 $S_{9} - S_{- 1}$ ，需要判断后一项不存在的情况

795

795. 前缀和 - AcWing题库

highlighter- cpp

#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int s[N];

int main() {
    int n, m;
    cin >> n >> m;
    int a;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a);
        s[i] = a + s[i - 1];
    }
    while (m--) {
        int l, r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

二维前缀和

计算各个S

$S_{x, y} = a_{i, j} + S_{i - 1, j} + S_{i, j - 1} - S_{i - 1, j - 1}$

计算子矩阵

$S_{(x_{1}, y_{1}), (x_{2}, y_{2})} = S_{x_{2}, y_{2}} - S_{x_{2}, y_{1} - 1} - S_{x_{1} - 1, y_{2}} + S_{x_{1} - 1, y_{1} - 1}$

796

796. 子矩阵的和 - AcWing题库

highlighter- cpp

#include 
#include 

using namespace std;

const int N = 1e3 + 10;

int S[N][N];

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    int a;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a);
            S[i][j] = a + S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1];
        }
    }
    while (q--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        int res = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1];
        cout << res << endl;
    }
    return 0;
}

一维差分

b为a的差分，a为b的前缀和。 $b_{1} = a_{1}$ , $b_{n} = a_{n} - a_{n - 1}$

前缀和转差分

假想前缀和全为0，此时差分全为0。然后模拟插入，即前缀和 [1,1] 元素加上 $a_{1}$ ，[2,2] 元素加上 $a_{2}$ ，[n,n] 元素加上 $a_{n}$

797

797. 差分 - AcWing题库

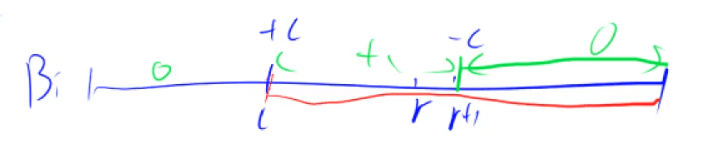
由 b 数组（差分）得到 a 数组（前缀和）O(n)

给 [L,R] 每个数加上 c，每次操作暴力方法 O(n)，使用差分 O(1)

highlighter- cpp

#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

void insert(int l, int r, int c) {
    b[l] += c;
    b[r + 1] -= c;
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    // 前缀和转差分
    for (int i = 1; i <= n; i++) {
        insert(i, i, a[i]);
    }
    int l, r, c;
    while (m--) {
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    // 差分转前缀和
    for (int i = 1; i <= n; i++) b[i] += b[i - 1];
    for (int i = 1; i <= n; i++) cout << b[i] << " ";
    return 0;
}

二维差分

构造 $b_{i j}$ 满足 $a_{i j} = \sum_{1}^{n} \sum_{1}^{m} b_{i j}$

子矩阵全加c

$b_{x_{1}, y_{1}} + = c b_{x_{2} + 1, y_{1}} - = c b_{x_{1}, y_{2} + 1} - = c b_{x_{2} + 1, y_{2} + 1} + = c$

前缀和转差分

假想前缀和全为0，此时差分全为0。然后模拟插入，即模拟子矩阵 [1 , 1][1 , 1] 加 c

798

798. 差分矩阵 - AcWing题库

highlighter- cpp

#include 
#include 

using namespace std;

const int N = 1e3 + 10;

int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) insert(i, j, i, j, a[i][j]);

    while (q--) {
        int x1, x2, y1, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) cout << b[i][j] << " ";
        cout << endl;
    }

    return 0;
}

双指针算法

用于把朴素算法优化到 O(n)

highlighter- gcode

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

第一类双指针

指向两个序列，用两个指针维护一段区间

第二类双指针

指向一个序列，如快排。维护某种次序，比如归并排序中合并两个有序序列的操作

799 ⭐⭐ 第一类

799. 最长连续不重复子序列 - AcWing题库

数据量 1e5 ，用数组统计出现次数。当数据量很大时用哈希表做

从朴素算法看 i，j 的单调关系，然后套用双指针。两个指针 [i,j] 维护一个最长不重复序列区间。i，j 一定是往右走的（单调性），若 i 往左走则与最长不重复序列区间矛盾。

highlighter- arduino

#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int a[N], b[N];

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    int count = 0;
    for (int i = 0, j = 0; j < n; j++) {
        b[a[j]]++;
        while (b[a[j]] > 1) {
            b[a[i]]--;
            i++;
        }
        count = max(j - i + 1, count);
    }
    cout << count;
    return 0;
}

800 第二类

800. 数组元素的目标和 - AcWing题库

highlighter- cpp

#include 
#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

int main() {
    int n, m, x;
    cin >> n >> m >> x;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < m; i++) {
        scanf("%d", &b[i]);
    }
    for (int i = 0, j = m - 1; i < n && a[i] < x; i++) {
        while (j >= 0 && b[j] > x - a[i]) j--;
        if (a[i] + b[j] == x) {
            cout << i << " " << j;
            break;
        }
    }
    return 0;
}

2816 第二类

2816. 判断子序列 - AcWing题库

由于堆数组初始化默认为0，如下输入会导致 i 最终为 2(i) 而不是 1(n)，在最后的判断中输出 No。因此向右移动 i 时需要添加一个 i 的条件，避免将数组外元素纳入判断。


powershell
1 2
1
1 0



highlighter-  cpp
#include 
#include 
#include 

using namespace std;

const int N = 1e6 + 10;

int a[N], b[N];

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < m; i++) {
        scanf("%d", &b[i]);
    }
    // i 是 a 指针，j 是 b 指针
    int i, j;
    for (i = 0, j = 0; j < m; j++) {
        if (i < n && a[i] == b[j]) i++;  // 注意 i < n
    }
    if (i == n)
        cout << "Yes";
    else
        cout << "No";
    return 0;
}



位运算
原码、反码、补码

原码 x = 00001010
反码 x = 11110101
补码 x = 11110110 （反码+1）

计算机底层实现没有减法，只能用加法来做减法


求某一位数字
highlighter-  apache
int i = a >> 2 & 1;



返回最后一位1 lowbit
highlighter-  stylus
a & (~a + 1) // 0000001000
// 整数x的负数是取反x后加1
// -a 等同 ~a+1
a & -a



801
801. 二进制中1的个数 - AcWing题库
highlighter-  cpp
#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

int a[N];

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        scanf("%d", &a[i]);
    }
    for (int i = 0; i < n; i++) {
        int count = 0;
        while (a[i]) {
            a[i] -= a[i] & -a[i];
            count++;
        }
        cout << count << " ";
    }
    return 0;
}



整数离散化
值域大 0 ~ 1e9，个数少 1e5。有些题目数组大小与值域一样大（如计数器），此时空间不够，需要整数离散化。如 A[1,3,10000] 映射为 B[1,2,3]，A默认有序

A 中可能有重复元素，需要去重
如何算出 x 离散化后的值，二分算第一个 >= x 元素在 A 中的位置 + 1

highlighter-  arduino
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n
}



802
802. 区间和 - AcWing题库
当数组下标小的时候可以用前缀和做，该题区间范围2e9（跨度大），但稀疏（元素少），可以先整数离散化，然后再前缀和
数组开30万(n+2m)，插入10万，查询20万
highlighter-  arduino
#include 
#include 
#include 
#include 
using namespace std;

typedef pair<int, int> PII;

const int N = 3e5 + 10;

// 差分
int s[N];

vector<int> alls;
vector add, query;

int find(int x) {
    int l = 0, r = alls.size() - 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (alls[mid] >= x)
            r = mid;
        else
            l = mid + 1;
    }
    return l + 1;
}

int main() {
    int n, m;
    cin >> n >> m;
    while (n--) {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});

        alls.push_back(x);
    }
    for (int i = 0; i < m; i++) {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        alls.push_back(l);
        alls.push_back(r);
    }
    // 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());

    // 插入
    for (auto item : add) {
        int x = find(item.first);
        s[x] += item.second;
    }

    // 差分转前缀和
    for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + s[i];

    // 处理询问
    for (auto item : query) {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }
    return 0;
}



unique
本质上是第一类双指针算法
highlighter-  arduino
#include 
#include 
#include 
#include 

using namespace std;

vector<int> a;

// a 升序序列，i 指针存放当前位置，j 遍历整个数组
vector<int>::iterator unique(vector<int>& a) {
    int i = 0;
    for (int j = 0; j < a.size(); j++) {
        if (!j || a[j - 1] != a[j]) a[i++] = a[j];
    }
    // a[0~i-1] 所有不同的数
    return a.begin() + i;
}

// vector::iterator unique(vector& a) {
//     int i = 1;
//     for (int j = 0; j < a.size(); j++) {
//         if (a[i - 1] != a[j]) a[i++] = a[j];
//     }
//     // a[0~i-1] 所有不同的数
//     return a.begin() + i;
// }

int main() {
    int n;
    cin >> n;
    for (int i = 0, x; i < n; i++) {
        scanf("%d", &x);
        a.push_back(x);
    }
    sort(a.begin(), a.end());
    auto x = unique(a);
    for (int i = 0; i < x - a.begin(); i++) {
        cout << a[i] << " ";
    }
    return 0;
}

powershell
5
1 2 2 3 3
1 2 3 



区间合并

按区间左端点排序
第二个区间对比第一个区间[st,ed]有三种情况

在区间内，不更新
与区间交集，ed更新
在区间外，st,ed更新，更新计数器



803
803. 区间合并 - AcWing题库
highlighter-  arduino
#include 
#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PLL;

vector a;

vector merge(vector &segs) {
    vector res;
    sort(segs.begin(), segs.end());
    int st = -2e9, ed = -2e9;
    for (auto seg : segs) {
        if (ed < seg.first) {
            if (st != -2e9) res.push_back({st, ed});
            st = seg.first;
            ed = seg.second;
        } else {
            ed = max(ed, seg.second);
        }
    }
    if (st != -2e9) res.push_back({st, ed});
    return res;
}

int main() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int l, r;
        cin >> l >> r;
        a.push_back({l, r});
    }

    auto res = merge(a);
    cout << res.size() << endl;
    return 0;
}



759 ⭐ ⭐ 格子染色（美团）
759. 格子染色 - AcWing题库

读入所有行操作，列操作，并排序
合并行区间，合并列区间
计算所有行的和 + 列的和 res
res 减去每个行与每个列之间重合点数量

highlighter-  arduino
#include 
#include 
#include 
#include 

using namespace std;

const int N = 1e5 + 10;

struct Node {
    int no, l, r;
    bool operator<(const Node& w) const {
        if (no != w.no)
            return no < w.no;
        else if (l != w.l)
            return l < w.l;
        else
            return r < w.r;
    }
};

// 用 vector> 会很慢
vector rows;
vector cols;

vector merge(vector segs) {
    vector res;
    int no = -2e9, st = -2e9, ed = -2e9;
    for (auto seg : segs) {
        if (st != -2e9 && no != seg.no) {
            res.push_back({no, st, ed});
            no = seg.no;
            st = seg.l;
            ed = seg.r;
        } else {
            no = seg.no;
            if (seg.l > ed) {
                if (st != -2e9) res.push_back({no, st, ed});
                st = seg.l;
                ed = seg.r;
            } else {
                ed = max(seg.r, ed);
            }
        }
    }
    if (ed != -2e9) res.push_back({no, st, ed});
    return res;
}

int main() {
    int n;
    cin >> n;
    // 步骤1 输入
    while (n--) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        if (x1 == x2) {
            rows.push_back({x1, min(y1, y2), max(y1, y2)});
        } else {
            cols.push_back({y1, min(x1, x2), max(x1, x2)});
        }
    }
    sort(rows.begin(), rows.end());
    sort(cols.begin(), cols.end());
    // 步骤2 合并区间
    rows = merge(rows);
    cols = merge(cols);
    // 步骤3 计算
    long long res = 0;  // 最大值可以是 (2e9)平方=4e18
    for (int i = 0; i < rows.size(); i++) {
        res += rows[i].r - rows[i].l + 1;
    }
    for (int i = 0; i < cols.size(); i++) {
        res += cols[i].r - cols[i].l + 1;
    }
    // 步骤4 去重
    for (int i = 0; i < rows.size(); i++) {
        for (int j = 0; j < cols.size(); j++) {
            auto row = rows[i];
            auto col = cols[j];
            if (row.l <= col.no && row.r >= col.no && col.l <= row.no &&
                col.r >= row.no)
                res--;
        }
    }
    cout << res;
    return 0;
}


   ios::sync_with_stdio(false)
快速排序
    785 ⭐
    786
归并排序
    787 ⭐
    788 ⭐⭐
整数二分
    左区间边界点
    右区间边界点
    mid分子加1
    789 ⭐
浮点数二分
    790 ⭐
高精度（整数运算）
    A + B
    A - B
    A *  b
    A / b
一维前缀和
    795
二维前缀和
    796
一维差分
    797
二维差分
    798
双指针算法
    第一类双指针
    第二类双指针
    799 ⭐⭐  第一类
    800 第二类
    2816 第二类
位运算
    原码、反码、补码
    求某一位数字
    返回最后一位1 lowbit
    801
整数离散化
    802
unique
区间合并
    803
    759 ⭐ ⭐ 格子染色（美团）
 
 
 
 
__EOF__

本文作者：小能正在往前冲

  本文链接： https://www.cnblogs.com/linxiaoxu/p/17671226.html 
  关于博主： 评论和私信会在第一时间回复。或者直接私信我。 
  版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！ 
  声援博主： 如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。

C++算法之旅、04 基础篇 | 第一章 基础算法

ios::sync_with_stdio(false)

快速排序

785 ⭐

786

归并排序

787 ⭐

788 ⭐⭐

整数二分

左区间边界点

右区间边界点

mid分子加1

789 ⭐

浮点数二分

790 ⭐

高精度（整数运算）

A + B

A - B

A * b

A / b

一维前缀和

795

二维前缀和

796

一维差分

797

二维差分

798

双指针算法

第一类双指针

第二类双指针

799 ⭐⭐ 第一类

800 第二类

2816 第二类

位运算

原码、反码、补码

求某一位数字

返回最后一位1 lowbit

801

整数离散化

802

unique

区间合并

803

759 ⭐ ⭐ 格子染色（美团）

C++算法之旅、04 基础篇 | 第一章基础算法