• 初阶数据结构（6）（队列的概念、常用的队列方法、队列模拟实现【用双向链表实现、用数组实现】、双端队列 (Deque)、OJ练习【用队列实现栈、用栈实现队列】）

    接上次博客：初阶数据结构（5）（栈的概念、栈的模拟实现、栈的应用及练习【改变元素的序列 、 将递归转化为循环、括号匹配、逆波兰表达式求值、出栈入栈次序匹配、最小栈】、链栈和顺序栈栈、虚拟机栈、栈帧的区别）_di-Dora的博客-CSDN博客

    目录

    队列(Queue)的概念

     常用的队列方法

    队列模拟实现

    我们先用双向链表来实现一个吧：

    现在考虑用数组实现：​

    双端队列 (Deque)

    OJ练习：

    1、用队列实现栈：

    2、用栈实现队列：

    队列(Queue)的概念

    队列是一种特殊的线性表，它只允许在一端进行插入数据操作，而在另一端进行删除数据操作。这个特性使得队列的数据按照先进先出（FIFO）的顺序进行处理。这意味着最先插入的元素将最先被删除，而最后插入的元素将最后被删除。

    在队列中，进行插入操作的一端称为队尾（Tail/Rear），新元素将被添加到队尾；而进行删除操作的一端称为队头（Head/Front），最早插入的元素将从队头被删除。

    这个过程就好像人们排队等候服务，先来的人先被服务，后来的人排在队尾等待。

    举个例子来说明队列的概念。假设有一个队列，初始时队列为空。现在按照顺序依次执行以下操作：

    • 将元素A插入队尾。
    • 将元素B插入队尾。
    • 将元素C插入队尾。
    • 删除队头元素。
    • 将元素D插入队尾。
    • 删除队头元素。

    在这个过程中，元素A首先被插入队尾，然后是元素B，再然后是元素C。当执行删除操作时，队头的元素A被删除。接着，元素D被插入队尾，然后队头的元素B被删除。

    根据队列的特性，删除操作总是在队头进行，而插入操作总是在队尾进行，确保了元素的顺序是先进先出的。

    队列在实际应用中具有广泛的应用，例如任务调度、消息传递、广度优先搜索等场景都可以使用队列来实现。

     

     在Java中，Queue是个接口，底层是通过链表实现的：

    注意：Queue是个接口，在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。 

    1. Deque queue2 = new LinkedList<>();
    2.  
    3. Queue queue1 = new LinkedList<>();

     常用的队列方法

    • boolean add(E element): 将元素添加到队列的尾部，如果队列已满则抛出异常。
    • boolean offer(E element): 将元素添加到队列的尾部，如果队列已满则返回false。
    • E remove(): 删除并返回队列头部的元素，如果队列为空则抛出异常。
    • E poll(): 删除并返回队列头部的元素，如果队列为空则返回null。
    • E element(): 返回队列头部的元素，如果队列为空则抛出异常。
    • E peek(): 返回队列头部的元素，如果队列为空则返回null。
    • int size(): 返回队列中的元素个数。
    • boolean isEmpty(): 判断队列是否为空。
    • boolean contains(Object element): 判断队列是否包含指定的元素。
    • void clear(): 清空队列中的所有元素。

    当然，除了上述方法，Queue接口还继承了Collection接口中的一些方法，如iterator()、addAll(Collection c)等。 

    我们可以试验一下这些方法：

    1. import java.util.Queue;
    2. import java.util.LinkedList;
    3.  
    4. public class QueueExample {
    5.     public static void main(String[] args) {
    6.         // 创建一个队列
    7.         Queue queue = new LinkedList<>();
    8.  
    9.         // 添加元素到队列
    10.         queue.add("Apple");
    11.         queue.offer("Banana");
    12.         queue.offer("Cherry");
    13.  
    14.         // 删除并返回队列头部的元素
    15.         String removedElement = queue.remove();
    16.         System.out.println("删除的元素: " + removedElement);
    17.  
    18.         // 返回队列头部的元素
    19.         String head = queue.element();
    20.         System.out.println("队列头部元素: " + head);
    21.  
    22.         // 判断队列是否为空
    23.         boolean isEmpty = queue.isEmpty();
    24.         System.out.println("队列是否为空: " + isEmpty);
    25.  
    26.         // 获取队列的大小
    27.         int size = queue.size();
    28.         System.out.println("队列大小: " + size);
    29.  
    30.         // 遍历队列并打印元素
    31.         System.out.println("队列元素: ");
    32.         for (String fruit : queue) {
    33.             System.out.println(fruit);
    34.         }
    35.  
    36.         // 判断队列是否包含指定的元素
    37.         boolean containsElement = queue.contains("Banana");
    38.         System.out.println("队列是否包含Banana: " + containsElement);
    39.  
    40.         // 清空队列
    41.         queue.clear();
    42.         System.out.println("清空后的队列大小: " + queue.size());
    43.     }
    44. }

     你有没有发现，最上面的几种方法好像有些功能上是重复的：

    你可以跳转到源代码去看一看英文的注解：

    所以我们可以把它们分为两组，这两组的差别如下：

    add(E element)和offer(E element)：

    add(E element): 将元素添加到队列的尾部。如果队列已满，抛出一个IllegalStateException异常。
    offer(E element): 将元素添加到队列的尾部。如果队列已满，则返回false

    区别：add()方法在无法添加元素时会抛出异常，而offer()方法在无法添加元素时返回false。

    remove()和poll()：

    remove(): 删除并返回队列头部的元素。如果队列为空，抛出一个NoSuchElementException异常。
    poll(): 删除并返回队列头部的元素。如果队列为空，则返回null。
     

    区别：remove()方法在队列为空时会抛出异常，而poll()方法在队列为空时返回null。

    element()和peek()：

    element(): 返回队列头部的元素，但不会删除它。如果队列为空，则抛出一个NoSuchElementException异常。

    peek(): 返回队列头部的元素，但不会删除它。如果队列为空，则返回null。

    区别：element()方法在队列为空时会抛出异常，而peek()方法在队列为空时返回null。

    总体上，这三组方法的功能相同，不同之处在于在特定情况下的异常处理方式。add()、remove()和element()方法在无法执行操作时会抛出异常，而offer()、poll()和peek()方法则会返回特定值来指示操作的成功与否。

    队列模拟实现

    队列中既然可以存储元素，那底层肯定要有能够保存元素的空间，我们通过前面线性表的学习了解到常见的空间类型有两种：顺序结构 和 链式结构。队列的实现使用顺序结构还是链式结构好？

    都可以，随意选。

    我们先用双向链表来实现一个吧：

    1. import java.util.List;
    2.  
    3. /**
    4.  * @Author 12629
    5.  * @Description：
    6.  */
    7. public class MyQueue {
    8.     static class ListNode {
    9.         private int val;
    10.         private ListNode prev;
    11.         private ListNode next;
    12.  
    13.         public ListNode(int val) {
    14.             this.val = val;
    15.         }
    16.     }
    17.  
    18.     private ListNode front;//队头
    19.     private ListNode rear;//队尾
    20.  
    21.     private int usedSize;
    22.  
    23.  
    24.  
    25.     //我们和源代码保持一致，用头插法
    26.     public void offer(int x) {
    27.         ListNode node = new ListNode(x);
    28.         if(front == null) {
    29.             front = rear = node;
    30.         }else {
    31.             node.next = front;
    32.             front.prev = node;
    33.             front = node;
    34.         }
    35.         usedSize++;
    36.     }
    37.  
    38.     //出队列 相当于 删除尾节点
    39.     //先进先出
    40.     public int poll() {
    41.         if(front == null) {
    42.             return -1; //抛异常也可以
    43.         }
    44.         int ret = rear.val;
    45.         if(front == rear) {
    46.             front = null;
    47.             rear = null;
    48.             usedSize--;
    49.             return ret;
    50.         }
    51.         rear = rear.prev;
    52.         rear.next = null;
    53.         usedSize--;
    54.         return ret;
    55.     }
    56.  
    57.     public int peek() {
    58.         if(front == null) {
    59.             return -1;
    60.         }
    61.         return front.val;
    62.     }
    63.  
    64.     public int getUsedSize() {
    65.         return usedSize;
    66.     }
    67.  
    68.     public boolean isEmpty() {
    69.         return usedSize == 0;
    70.     }
    71. }
    1.     public static void main(String[] args) {
    2.     MyQueue myQueue = new MyQueue();
    3.     myQueue.offer(1);
    4.     myQueue.offer(2);
    5.     myQueue.offer(3);
    6.     myQueue.offer(4);
    7.     // 4   3   2   1
    8.  
    9.     System.out.println(myQueue.poll());
    10.     System.out.println(myQueue.poll());
    11.     System.out.println(myQueue.poll());
    12.     System.out.println(myQueue.poll());
    13.     System.out.println(myQueue.poll());
    14.     System.out.println(myQueue.poll());
    15.     }

    来来来，做个选择题，看看你是不是理解了：

    下列关于队列的叙述错误的是( )

    A.队列可以使用链表实现

    B.队列是一种"先入先出"的数据结构

    C.数据出队列时一定只影响队尾引用

    D.数据入队列时一定从尾部插入

     答案： C.数据出队列时一定只影响队尾引用

    C的说法是错误的。数据出队列时会同时影响队头和队尾引用。

    在队列中，数据的插入（入队列）是在队尾进行的，而数据的删除（出队列）是在队头进行的。当数据出队列时，队头引用会更新为下一个元素，同时队尾引用也可能需要进行更新，特别是当队列中只有一个元素时，出队列后队尾引用会变为null或者空值。

    现在考虑用数组实现：

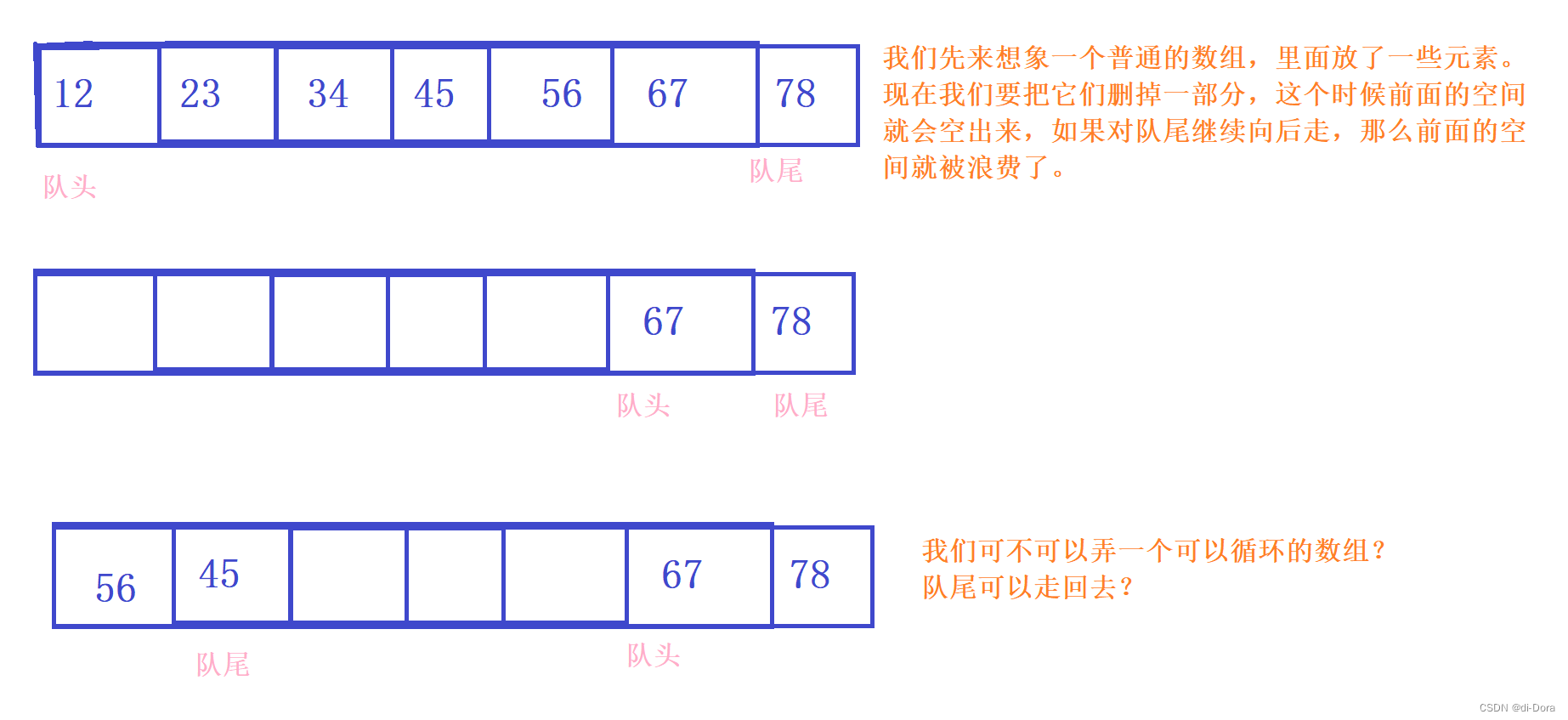
     就像是一个“开心大转盘”，或者一个飞镖靶子（订奖品的那种）：

     数组下标循环的小技巧 ：

    1. 下标最后再往后(offset 小于 array.length): index = (index + offset) % array.length。

     2. 下标最前再往前(offset 小于 array.length): index = (index + array.length - offset) % array.length。

    看看掌握程度：

    现有一循环队列，其队头为front，队尾为rear，循环队列长度为N,最多存储N-1个数据。其队内有效长度为（ ）

    A.(rear - front + N) % N + 1
    B.(rear - front + N) % N
    C.(rear - front) % (N + 1)
    D.(rear - front + N) % (N - 1) 

    答案：A

    这样就已经排除两个了， 我们再来了解一下 A 的原理：

     A. (rear - front + N) % N + 1:

    这是计算循环队列队内有效长度的公式。解释如下：

    (rear - front + N) % N：首先计算rear和front之间的差值，即队尾和队头的相对位置。由于循环队列的特性，rear可能小于front（表示循环回到队列的开头），因此需要加上N来确保差值为正数。然后再进行取模运算，将差值限定在0到N-1之间。

    1：由于队内有效长度是指队列中实际存储的元素个数，需要将前面计算得到的差值加1，即为队内有效长度。

    因此，选项A使用了合适的公式来计算循环队列的队内有效长度。

    力扣：622. 设计循环队列 - 力扣（Leetcode） 

    我们看一下这个代码的具体要求：

    1. class MyCircularQueue {
    2.  
    3.     public MyCircularQueue(int k) {
    4.  
    5.     }
    6.     
    7.     public boolean enQueue(int value) {
    8.  
    9.     }
    10.     
    11.     public boolean deQueue() {
    12.  
    13.     }
    14.     
    15.     public int Front() {
    16.  
    17.     }
    18.     
    19.     public int Rear() {
    20.  
    21.     }
    22.     
    23.     public boolean isEmpty() {
    24.  
    25.     }
    26.     
    27.     public boolean isFull() {
    28.  
    29.     }
    30. }
    1. class MyCircularQueue {
    2.  
    3.     private int[] elem;
    4.     private int front;//队头下标
    5.     private int rear;//队尾下标
    6.  
    7.     public MyCircularQueue(int k) {
    8.         this.elem = new int[k+1]; //因为会浪费空间，所以为了确保数组不会越界，多给一个空间
    9.     }
    10.  
    11.     public boolean enQueue(int value) {
    12.         if(isFull()) {
    13.             return false;
    14.         }
    15.         elem[rear] = value;
    16.         rear = (rear+1)%elem.length; //可不能 rear++，会越界！
    17.         return true;
    18.     }
    19.  
    20.     public boolean deQueue() {
    21.         //1、空的 不能出
    22.         if(isEmpty()) {
    23.             return false;
    24.         }
    25.         //2、不空 则 保存队头元素 然后front往后走
    26.         front = (front+1)%elem.length;
    27.         return true;
    28.     }
    29.  
    30.     //得到队头元素
    31.     public int Front() {
    32.         if(isEmpty()) {
    33.             return -1;
    34.         }
    35.         return elem[front];
    36.     }
    37.  
    38.     public int Rear() {
    39.         if(isEmpty()) {
    40.             return -1;
    41.         }
    42.         int index = (rear == 0) ? elem.length-1 : rear-1;
    43.         return elem[index];
    44.         //return elem[(rear - 1 + elem.length) % elem.length];
    45.     }
    46.  
    47.     public boolean isEmpty() {
    48.         return front == rear;
    49.     }
    50.  
    51.     public boolean isFull() {
    52.         //rear的下一个是front
    53.         if((rear+1)%elem.length == front) {
    54.             return true;
    55.         }
    56.         return false;
    57.     }
    58. }

    return elem[(rear - 1 + elem.length) % elem.length]：由于rear指向队尾的下一个位置，所以要获取队尾元素的索引，需要将rear减1。然后加上elem.length，是为了处理rear-1为负数的情况，确保索引为正数。最后再进行取模运算，将索引限制在0到capacity-1之间，实现循环。
    elem[...]：通过计算得到的索引，访问elements数组中对应位置的元素，即为队尾元素的值。

    如下是使用链表的方法，是力扣的官方题解：

    1. class MyCircularQueue {
    2.     private ListNode head;
    3.     private ListNode tail;
    4.     private int capacity;
    5.     private int size;
    6.  
    7.     public MyCircularQueue(int k) {
    8.         capacity = k;
    9.         size = 0;
    10.     }
    11.  
    12.     public boolean enQueue(int value) {
    13.         if (isFull()) {
    14.             return false;
    15.         }
    16.         ListNode node = new ListNode(value);
    17.         if (head == null) {
    18.             head = tail = node;
    19.         } else {
    20.             tail.next = node;
    21.             tail = node;
    22.         }
    23.         size++;
    24.         return true;
    25.     }
    26.  
    27.     public boolean deQueue() {
    28.         if (isEmpty()) {
    29.             return false;
    30.         }
    31.         ListNode node = head;
    32.         head = head.next;  
    33.         size--;
    34.         return true;
    35.     }
    36.  
    37.     public int Front() {
    38.         if (isEmpty()) {
    39.             return -1;
    40.         }
    41.         return head.val;
    42.     }
    43.  
    44.     public int Rear() {
    45.         if (isEmpty()) {
    46.             return -1;
    47.         }
    48.         return tail.val;
    49.     }
    50.  
    51.     public boolean isEmpty() {
    52.         return size == 0;
    53.     }
    54.  
    55.     public boolean isFull() {
    56.         return size == capacity;
    57.     }
    58. }
    59.

    来做个小练习： 

    对于循环队列，下列叙述中正确的是 （）

    A.队头是固定不变的
    B.队头一定大于队尾
    C.队头一定小于队尾
    D.队头可以大于队尾，也可以小于队尾 

    答案：D、队头可以大于队尾，也可以小于队尾

    解析：对于循环队列，队头和队尾的相对位置是可以变化的。循环队列通过使用取模运算来实现循环的效果，当队尾达到数组的末尾时，下一个元素将回到数组的开头。这样可以利用数组的空间进行循环利用。

    在循环队列中，队头可以在队尾之后，也可以在队尾之前，这取决于队列中元素的个数和队列的操作历史。例如，当队列为空时，队头和队尾指向同一个位置，队列中只有一个元素；当队列已满时，队头可能在队尾之后。

    因此，选项D中的说法是正确的，循环队列中队头可以大于队尾，也可以小于队尾。

    双端队列 (Deque)

    双端队列（Deque）是一种数据结构，它允许在队列的两端进行插入和删除操作。其名称"Deque"是"double ended queue"的缩写。双端队列可以被视为同时具有队列和栈的性质，因为它允许在队列的两端进行元素的添加和移除。

    双端队列与普通队列的主要区别在于，普通队列只允许在队尾进行入队操作，并且只能从队头进行出队操作。而双端队列允许在队头和队尾同时进行入队和出队操作。

    双端队列的特性使得它在许多场景下非常有用。下面是一些双端队列的常见应用场景：

    • 队列和栈的结合：双端队列可以用作队列或栈的替代品。你可以选择从队头或队尾插入和删除元素，从而灵活地应对不同的需求。
    • 路径搜索算法：在某些路径搜索算法（如广度优先搜索）中，需要在搜索过程中同时从前面和后面进行扩展。双端队列提供了高效的操作，使得这样的算法更容易实现。
    • 滑动窗口问题：滑动窗口问题是一类常见的算法问题，通常涉及到在一个固定大小的窗口内进行计算。双端队列可以用来维护窗口内的元素，并且能够在常数时间内进行插入和删除操作。

    双端队列的实现方式有多种，可以使用数组、链表或双向链表来实现。具体选择哪种实现方式取决于应用场景和性能要求。无论使用何种实现方式，双端队列的操作复杂度应该尽量为O(1)。

    下面是双端队列的一些常见操作：

    • 入队操作（从队头或队尾插入元素）：可以通过 insertFront() 和 insertLast() 等方法来实现。
    • 出队操作（从队头或队尾删除元素）：可以通过 deleteFront() 和 deleteLast() 等方法来实现。
    • 获取队头和队尾元素：可以通过 getFront() 和 getLast() 等方法来获取队头和队尾元素的值，而不进行删除操作。
    • 判断双端队列是否为空：可以通过 isEmpty() 方法来判断双端队列是否为空。

    总而言之，双端队列是一种非常有用的数据结构，它允许在队列的两端进行插入和删除操作。它可以灵活地应对不同的应用场景，并且能够以常数时间复杂度进行插入和删除操作。

    1. Deque stack = new ArrayDeque<>();//双端队列的线性实现
    2. Deque queue = new LinkedList<>();//双端队列的链式实现

     ArrayDeque<>() 是 Deque 的数组实现：跳转过去看看：

     ArrayDeque的介绍：

    ArrayDeque是Java中的一个双端队列（deque）实现类。

    它实现了Deque接口，允许在队列两端进行快速插入和删除操作。

    双端队列是一种具有队列和栈特性的数据结构，可以在队列的两端进行元素的插入和删除。ArrayDeque使用动态数组作为其内部实现，它可以根据需要自动调整大小。

    与LinkedList相比，ArrayDeque提供了更高效的随机访问和更快的插入/删除操作。然而，ArrayDeque在插入和删除操作中的开销较高，需要移动其他元素来保持队列的连续性。

    以下是ArrayDeque常用的一些方法：

    • addFirst(element)：将元素添加到队列的开头。
    • addLast(element)：将元素添加到队列的末尾。
    • removeFirst()：移除并返回队列的第一个元素。
    • removeLast()：移除并返回队列的最后一个元素。
    • peekFirst()：返回队列的第一个元素，但不移除它。
    • peekLast()：返回队列的最后一个元素，但不移除它。
    • size()：返回队列中元素的数量。

    ArrayDeque可以用于实现双向队列、栈、循环队列等数据结构，并且它是线程不安全的，不支持多线程并发操作。如果需要在多线程环境下使用队列，可以考虑使用ConcurrentLinkedDeque等线程安全的实现类。

    1.         Deque stack = new ArrayDeque<>();//双端队列的线性实现
    2.         
    3.         stack.push(1);  //双端队列实现的栈

    OJ练习：

    1、用队列实现栈：

    请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。
    实现 MyStack 类：

    • void push(int x) 将元素 x 压入栈顶。
    • int pop() 移除并返回栈顶元素。
    • int top() 返回栈顶元素。
    • boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

    力扣：225. 用队列实现栈 - 力扣（Leetcode） 

    我想先问你一个问题：我们最普通的队列可以实现一个栈吗？

    答案是否定的。

     

     好了，现在来实现一下：

    1. import java.util.LinkedList;
    2. import java.util.Queue;
    3.  
    4. public class MyStack {
    5.  
    6.     private Queue qu1;
    7.     private Queue qu2;
    8.  
    9.     public MyStack() {
    10.         qu1 = new LinkedList<>();
    11.         qu2 = new LinkedList<>();
    12.     }
    13.  
    14.     /*
    15.      * 入栈操作：
    16.      * 入到不为空的队列当中，如果都为空 入到qu1
    17.      */
    18.     public void push(int x) {
    19.         if(!qu1.isEmpty()) {
    20.             qu1.offer(x);
    21.         }else if(!qu2.isEmpty()) {
    22.             qu2.offer(x);
    23.         }else {
    24.             qu1.offer(x);
    25.         }
    26.     }
    27.  
    28.     public int pop() {
    29.         if(empty()) {
    30.             return -1;//栈为空的
    31.         }
    32.  
    33.         if(!qu1.isEmpty()) {
    34.             int size = qu1.size();
    35.             for (int i = 0; i < size-1; i++) {
    36.                 int tmp = qu1.poll();
    37.                 qu2.offer(tmp);
    38.             }
    39.             return qu1.poll();
    40.         }else {
    41.             int size = qu2.size();
    42.             for (int i = 0; i < size-1; i++) {
    43.                 int tmp = qu2.poll();
    44.                 qu1.offer(tmp);
    45.             }
    46.             return qu2.poll();
    47.         }
    48.     }
    49.  
    50.     //peek
    51.     public int top() {
    52.         if(empty()) {
    53.             return -1;//栈为空的
    54.         }
    55.         int tmp = -1;
    56.         if(!qu1.isEmpty()) {
    57.             int size = qu1.size();
    58.             for (int i = 0; i < size; i++) {
    59.                 tmp = qu1.poll();
    60.                 qu2.offer(tmp);
    61.             }
    62.             return tmp; //最后一次覆盖掉 tmp 的值就是我们栈顶的元素
    63.         }else {
    64.             int size = qu2.size();
    65.             for (int i = 0; i < size; i++) {
    66.                 tmp = qu2.poll();
    67.                 qu1.offer(tmp);
    68.             }
    69.             return tmp;
    70.         }
    71.     }
    72.  
    73.     /*
    74.      * 2个队列都为空 表示 栈为空 ！！
    75.      *
    76.      */
    77.     public boolean empty() {
    78.         //2个对列 都为空的时候
    79.         return qu1.isEmpty() && qu2.isEmpty();
    80.     }
    81. }

    注意！！！ pop() 我这样写可不可以？

    1. if(!qu1.isEmpty()) {
    2.     for (int i = 0; i < qu1.size()-1; i++) {
    3.          int tmp = qu1.poll();
    4.          qu2.offer(tmp);
    5.     }
    6.     return qu1.poll();
    7.  }else {
    8.     for (int i = 0; i < qu2.size()-1; i++) {
    9.                 int tmp = qu2.poll();
    10.                 qu1.offer(tmp);
    11.     }
    12.     return qu2.poll();
    13. }

    当然不可以！！！

    因为我们每次 poll ，qu1 和 qu2 的 size 都会改变，是一个变量。

    2、用栈实现队列：

    力扣：232. 用栈实现队列 - 力扣（Leetcode）

    请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：
    实现 MyQueue 类：

    • void push(int x) 将元素 x 推到队列的末尾
    • int pop() 从队列的开头移除并返回元素
    • int peek() 返回队列开头的元素
    • boolean empty() 如果队列为空，返回 true ；否则，返回 false

    我们的思路如下：用输出栈和输入栈进行模拟，入队的时候把所有元素全部放到输入栈当中，出队的时候，把输入栈当中的所有元素全部倒回输出栈中，输出输出栈栈顶的元素：

    1. import java.util.Stack;
    2.  
    3. public class Myqu{
    4.     private Stack stack1; // 输入栈
    5.     private Stack stack2; // 输出栈
    6.  
    7.     public Myqu() {
    8.         stack1 = new Stack<>();
    9.         stack2 = new Stack<>();
    10.     }
    11.  
    12.     public void push(int x) {
    13.         // 将stack2中的元素全部转移到stack1
    14.         while (!stack2.isEmpty()) {
    15.             stack1.push(stack2.pop());
    16.         }
    17.         stack1.push(x);
    18.     }
    19.  
    20.     private void shiftStacks() {
    21.         if (stack2.isEmpty()) {
    22.             // 当输出栈为空时，将输入栈中的元素转移到输出栈
    23.             while (!stack1.isEmpty()) {
    24.                 stack2.push(stack1.pop());
    25.             }
    26.         }
    27.     }
    28.  
    29.     public int pop() {
    30.         shiftStacks(); // 确保输出栈中有元素
    31.         return stack2.pop(); // 从输出栈弹出元素
    32.     }
    33.  
    34.     public int peek() {
    35.         shiftStacks(); // 确保输出栈中有元素
    36.         return stack2.peek(); // 返回输出栈顶元素
    37.     }
    38.  
    39.     public boolean empty() {
    40.         return stack1.isEmpty() && stack2.isEmpty(); // 队列为空的条件是输入栈和输出栈都为空
    41.     }
    42.  
    43.     public static void main(String[] args) {
    44.         Myqu obj = new Myqu();
    45.         obj.push(1);
    46.         obj.push(2);
    47.         int param_2 = obj.pop();
    48.         int param_3 = obj.peek();
    49.         boolean param_4 = obj.empty();
    50.         System.out.println(param_2);  // 输出：1
    51.         System.out.println(param_3);  // 输出：2
    52.         System.out.println(param_4);  // 输出：false
    53.     }
    54. }

  • 相关阅读:
    教你微信小程序商城搭建-技术文章
    【全开源】进销存订货通管理系统（FastAdmin+ThinkPHP+Layui）
    我眼中的大数据（三）——MapReduce
    Python使用模拟退火（Simulated Annealing）算法构建优化器获取机器学习模型最优超参数组合（hyperparameter）实战+代码
    解决vue-cli node-sass安装不成功问题
    【C++】C++入门(一)
    CentOS 7 上编译和安装 SQLite 3.9.0
    【python入门篇】列表简介及操作（2）
    HTTP 参数污染 (HPP) 和 HTTP 参数碎片 (HPF)
    Windows-vscode安装与简单配置
  • 原文地址：https://blog.csdn.net/m0_74343467/article/details/130899108