2023 (ICPC) Jiangxi Provincial Contest -- Official Contest

A. Drill Wood to Make Fire

 输出即可

#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
const int N=1100;
typedef pair<int,int>pii;
 
int m,n;
int a[N][N];
 
void solve()
{
    int s,v,n;
    cin>>n>>s>>v;
    if(s*v>=n)
    cout<<1<<endl;
    else cout<<0<<endl;
}
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;cin>>t;
    while(t--)solve();
    return 0;
}

I. Tree

题意：给你一颗有个节点的树，你有两个操作

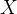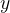第一个操作：将和之间的边权

第二个操作输出与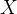直接相连的边的异或和

思路：因为异或是不进位加法，所以我们可以直接将树上每一条直接相连的边的异或值保存下来

然后需要修改的时候就可以直接修改

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
typedef pair<int,int>pii;
int n,q;
 
void solve()
{
    int a[N];
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)a[i]=0;
    for(int i=1;i<n;i++)
    {
        int x,y,w;
        scanf("%d%d%d",&x,&y,&w);
        a[x]^=w;
        a[y]^=w;
    }
    while(q--)
    {
        int op;
        scanf("%d",&op);
        if(op==1)
        {
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            a[x]^=z;
            a[y]^=z;
        }
        else
        {
            int x;
            scanf("%d",&x);
            printf("%d\n",a[x]);
        }
    }
 
}
 
int main()
{
    int t=1;
    while(t--)solve();
    return 0;
}

J. Function

题意：给你形如的二次函数，有两个操作

一个操作是增加一个二次函数。

另一个是查询当的时候函数值最小是多少

思路：因为是二次函数我们假设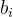是固定的我们就可以观察出，只要让

就可以发现最小值就可能在附近，所以我们只要查询附近的函数值即可

代码：

#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
const int N=110000;
typedef pair<int,int>pii;
 
int m,n;
int v[N];
void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>v[i];
    cin>>m;
    int t=  ::sqrt(1.0*n);
    while(m--)
    {
        int op;
        cin>>op;
        if(op)
        {
            int a;
            cin>>a;
            int minv=0x3f3f3f3f;
           for(int i=a-sqrt(n);i<=a+sqrt(n)+1;i++)
           {
               if(i>=0&&i<=n&&v[i])minv=min(minv,(i-a)*(i-a)+v[i]);
           }
            cout<<minv<<endl;
        }
        else
        {
            int a,b;
            cin>>a>>b;
            if(v[a])
            v[a]=min(v[a],b);
            else v[a]=b;
        }
    }
}
 
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;//cin>>t;
    while(t--)solve();
    return 0;
}

K. Split

题意：给你一个非递增加序列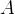，有两种操作

第一个操作，给你一个，使得

第二个操作，将序列分成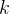个小块，其中每个小块的最大值-最小值之和要最小，并且输出每个小块中最大值-最小值之和最小值

思路：

首先看操作2，由于是递减序列每个块中的最小值都是分界线的左边，而分界线的右边就是下一个块中最大值，换句话说，如果有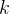个块那么我们可以写成

将公式转化一下变成， 

后面的刚好构成了差分数组，而因为序列是递减的我们可以保证一定是正的，而后面差分数我们要保证尽可能的小，这样答案才会小，所以我们将对他进行排序然后依次枚举即可。

然后再看修改操作

我们枚举出第项，

修改后，

然后对他进行差分,

得到 差分数组仅仅只是交换了个位置，并不会对答案有变化。

所以时间复杂度是

代码：

#include<bits/stdc++.h>
#define int long long
#define x first
#define y second
using namespace std;
const int N=1100000;
typedef pair<int,int>pii;
 
int k,m,n;
int a[N];
int d[N];
 
void solve()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    for(int i=1;i<n;i++)
        d[i]=a[i]-a[i-1];
    sort(d+1,d+n);
    for(int i=1;i<n;i++)
        d[i]=d[i-1]+d[i];
 
    cin>>m;
    while(m--)
    {
        int op,x;
        cin>>op>>x;
        if(op==1)
        {
            cout<<a[0]-a[n-1]+d[x-1]<<endl;
        }
    }
}
 
signed main()
{
    ios::sync_with_stdio(false);
    int t=1;//cin>>t;
    while(t--)solve();
    return 0;
}

L. Zhang Fei Threading Needles - Thick with Fine

输出N-1即可