多特征线性回归

在单特征线性回归模型中，我们通过一个特征对目标变量进行预测，例如通过房子的大小来预测房价。但实际现实生活中，影响房价的因素往往不止面积一个，例如还有房间数、楼层、位置等等，所以我们需要用到多特征的模型来对房价进行预测。

一、规定符号

xj：第j个特征

n：特征的数量

x(i)：第i个训练样本，是一个包含n个特征的行向量

xj(i)：表示第i个样本的第j个特征

二、模型

三、向量化

使用向量化可以简化模型，减少计算量和代码量，提升代码的执行速度。

四、梯度下降

五、正规方程

线性回归中一种寻找参数w、b的方式，该方法不用进行多次迭代梯度下降，直接使用高级线性代数知识求解。但是正规方程无法推广到其他机器学习算法，且当样本特征数量非常大时，运行速度非常慢。某些机器学习库会在后台使用这种方法解出w、b，但是大多数情况下都不会使用。

六、特征缩放

1、什么是特征缩放？

特征缩放是机器学习中一项重要的技术，可大大提升梯度下降的速度。

在预测房价的例子中，假设有两个影响房价的特征，面积和房间数，面积的取值范围是300-5000，房间数的取值范围是0-5，我们会发现面积和房间数的取值范围相差过大。当我们选择参数时，如果面积的参数（也称为权重）较大而房间数的参数较小，这样会导致最终预测的价格与实际的价格偏差较大，因为面积因素占的权重较大，对房价的影响占主要部分。为预测更精准，面积的参数应该选择较小的，房间数的参数应该选择较大的。

特征缩放对梯度下降会产生很大的影响，如图

特征的范围差异过大时，在散点图中，样本点都集中特征范围较大的那一侧，在在成本函数等高线图中，图形变得长且窄，梯度下降很可能越过全局最小值左右横跳。

2、如何实现特征缩放？

1、最大值

2、均值归一化

3、Z-score标准化（Z-score归一化/规范化）

     注：分母为该特征的标准差

3、特征缩放的范围

七、判断梯度下降是否收敛

1、绘制学习曲线

通过绘制成本函数学习曲线图，可直观地观察到梯度下降是否收敛，同时也可观察到趋于收敛时的迭代次数。

2、自动收敛测试

设置一个很小的值e，例如令它为0.001，判断每一次梯度下降对成本函数的改变是否小于或等于这个极小值，如果是则说明梯度下降现在比较平缓，也就是趋于收敛。但这个极小值e是很难选择的，所以一般更推荐绘制学习曲线。

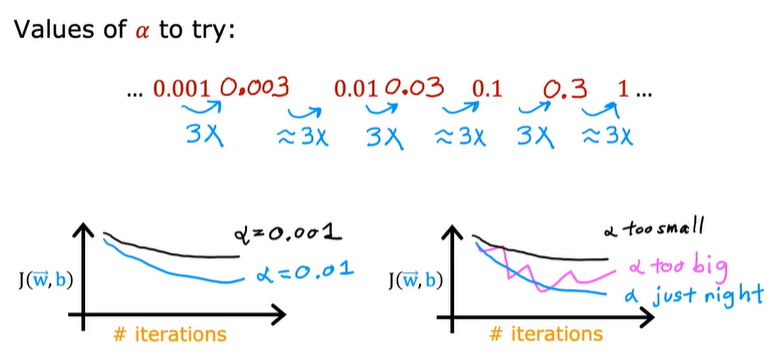
八、选择合适的学习率

当学习率过小时，下降的步子过小，导致到达最低点需要很多步，需要的时间也更多；

当学习率过大时，下降的步子较大，可能越过最低点，导致越来越远，甚至永远也到达不了最低点。

为什么我们可以采用固定的学习率？因为越靠近最低点，斜率将会越来越小，等于迈的步子越来越小了，最终也会慢慢靠近最低点。

如何选择合适的学习率呢？通常，可使用一些常见的值例如0.001、0.01、0.1、1.......，每次将学习率提高十倍，再结合学习曲线来判断学习率是否得当。

九、特征工程

特征工程指的是为算法选择或设计最合适的特征。

例如在预测房价的例子中，房子有长和宽两个特征，但是我们知道房子的面积是等于长乘以宽，因此会预感到面积更能预测房价，因此我们可以构建一个新的特征即面积，加入到模型中。

我们可以结合知识以及实际设计新的特征，使其帮助算法更简单、更准确的做出预测。

十、多项式回归

在此之前，我们都是选择使用直线来拟合数据集，但是在有的情况下，使用曲线或其他函数可能更好的拟合数据集，所以就需要采用多项式回归。例如，模型中包含二次项、三次项、根号项等，根据实际情况构造合适的多项式，使其更好地拟合。

十一、实现

部分数据集合和代码

 2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
......

 import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
 
alpha = 0.01  # 学习速率α
iters = 1000  # 要执行的迭代次数。
 
path = './data/ex1data2.txt'
data = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
data.head()  # 输出前五行
 
# 特征缩放
data = (data - data.mean()) / data.std()  # Z-score标准化
# data = (data - data.max()) / (data.max() - data.min())  # max-min归一化
# data = data / (np.abs(data.max()))  # MaxAbs标准化
 
# 在训练集中添加一列，以便我们可以使用向量化的解决方案来计算代价和梯度
data.insert(0, 'One', 1)
 
# 获取列数
cols = data.shape[1]
 
X = data.iloc[:, 0:cols - 1]  # 所有行，不包含最后一列
y = data.iloc[:, cols - 1:cols]  # 所有行,只包含最后一列
 
# np.matrix()函数用于从类数组对象或数据字符串返回矩阵
X = np.matrix(X.values)
y = np.matrix(y.values)
 
# 初始化参数矩阵
theta = np.matrix(np.array([0, 0, 0]))  # 1x3矩阵
 
 
def computeCost(X, y, theta):
    """代价函数"""
    num = len(X)
    inner = np.power(((X * theta.T) - y), 2)
    cost = np.sum(inner) / (2 * num)
    return cost
 
 
def gradientDescent(X, y, theta, alpha, iters):
    """梯度下降"""
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)
 
    for i in range(iters):
        error = (X * theta.T) - y
 
        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
 
        theta = temp
        cost[i] = computeCost(X, y, theta)
 
    return theta, cost
 
 
def normalEqn(X, y):
    """正规方程"""
    # np.linalg.inv()：矩阵求逆
    theta = np.linalg.inv(X.T @ X) @ X.T @ y  # @等价于 X.T.dot(X)
    return theta.T
 
 
# 执行梯度下降
g, cost = gradientDescent(X, y, theta, alpha, iters)
 
# 使用正规方程求参
g1 = normalEqn(X, y)  
cost1 = computeCost(X, y, g1)
 
# 未训练前的代价
print("梯度下降代价值：", computeCost(X, y, g))
print("正规方程代价值：", computeCost(X, y, g1))
 
# 绘制训练曲线
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

相关阅读:
专题一：双指针【优选算法】
Python数据分析案例10——北向资金流入与沪深300涨跌幅分析
 第十章配置数据库（二）
java 显示c控制台程序窗口,Windows-如何清除C中的控制台屏幕？
pinia中使用@vueuse/core库的useStorage做数据的持久化存储
 HTML 颜色名：网页设计的调色板
 Django（2）模板、标签
 软件测试面试，一定要准备的7个高频面试题（附答案，建议收藏）
three.js(二)：webpack + three.js + ts
优化改进YOLOv5算法之添加DCNv3模块，有效提升目标检测效果
原文地址：https://www.cnblogs.com/dxmstudy/p/17148181.html

	2104,3,399900
	1600,3,329900
	2400,3,369000
	1416,2,232000
	3000,4,539900
	1985,4,299900
	1534,3,314900
	1427,3,198999
	1380,3,212000
	1494,3,242500
	1940,4,239999
	2000,3,347000
	1890,3,329999
	4478,5,699900
	1268,3,259900
	......

	import numpy as np
	import pandas as pd
	import matplotlib.pyplot as plt


	alpha = 0.01 # 学习速率α
	iters = 1000 # 要执行的迭代次数。

	path = './data/ex1data2.txt'
	data = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
	data.head() # 输出前五行

	# 特征缩放
	data = (data - data.mean()) / data.std() # Z-score标准化
	# data = (data - data.max()) / (data.max() - data.min()) # max-min归一化
	# data = data / (np.abs(data.max())) # MaxAbs标准化

	# 在训练集中添加一列，以便我们可以使用向量化的解决方案来计算代价和梯度
	data.insert(0, 'One', 1)

	# 获取列数
	cols = data.shape[1]

	X = data.iloc[:, 0:cols - 1] # 所有行，不包含最后一列
	y = data.iloc[:, cols - 1:cols] # 所有行,只包含最后一列

	# np.matrix()函数用于从类数组对象或数据字符串返回矩阵
	X = np.matrix(X.values)
	y = np.matrix(y.values)

	# 初始化参数矩阵
	theta = np.matrix(np.array([0, 0, 0])) # 1x3矩阵


	def computeCost(X, y, theta):
	"""代价函数"""
	num = len(X)
	inner = np.power(((X * theta.T) - y), 2)
	cost = np.sum(inner) / (2 * num)
	return cost


	def gradientDescent(X, y, theta, alpha, iters):
	"""梯度下降"""
	temp = np.matrix(np.zeros(theta.shape))
	parameters = int(theta.ravel().shape[1])
	cost = np.zeros(iters)

	for i in range(iters):
	error = (X * theta.T) - y

	for j in range(parameters):
	term = np.multiply(error, X[:, j])
	temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))

	theta = temp
	cost[i] = computeCost(X, y, theta)

	return theta, cost


	def normalEqn(X, y):
	"""正规方程"""
	# np.linalg.inv()：矩阵求逆
	theta = np.linalg.inv(X.T @ X) @ X.T @ y # @等价于 X.T.dot(X)
	return theta.T


	# 执行梯度下降
	g, cost = gradientDescent(X, y, theta, alpha, iters)

	# 使用正规方程求参
	g1 = normalEqn(X, y)
	cost1 = computeCost(X, y, g1)

	# 未训练前的代价
	print("梯度下降代价值：", computeCost(X, y, g))
	print("正规方程代价值：", computeCost(X, y, g1))

	# 绘制训练曲线
	fig, ax = plt.subplots(figsize=(12, 8))
	ax.plot(np.arange(iters), cost, 'r')
	ax.set_xlabel('Iterations')
	ax.set_ylabel('Cost')
	ax.set_title('Error vs. Training Epoch')
	plt.show()