深度解读面试题：链表中环的入口结点（附代码，可过在线OJ）

在解读“链表中环的入口结点”前，我认为有必要明白关于它的一些用于打基础的问题（相交链表、判断链表中是否存在环）

相交链表

题目：

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。点击此处🤔前往该题
例如：

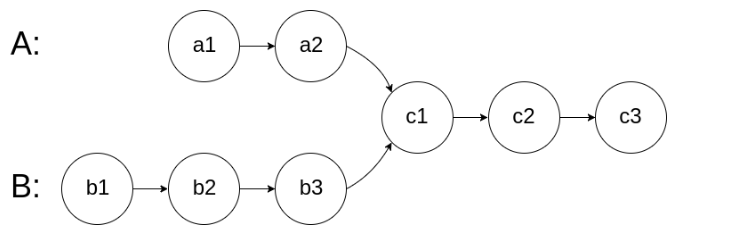
为了方便描述这类问题，我们给出更为抽象的逻辑图

首先我们第一眼能够想到的办法，就是遍历一遍然后一一进行比较。遍历的思路，以上图为例，将A中每个结点逐个和B中的结点进行比较，如果相等，那么该结点便是这两个链表的相交结点。（取部分讲解，A中的c1与B中的b1比较不相等，c1与b2比较不相等， c1与b3比较不相等，c1与c1比较相等！所以c1就是A和B的相交结点）。经过分析，可知这样的算法时间复杂度高达O(n2)。

通常的做法是
（1）获得两个链表的长度之差gap。
（2）长的链表从头开始，先走gap步
（3）长链表从第（2）步的位置开始，短的链表从头开始，一起往后走
（4）第一次遇到相等的结点了，该结点就是两个链表的相交结点

另外，在统计这两个链表各自的长度，获取差距步数的同时，可以判断这两个链表是否为相交的链表。判断的方式，两个链表的尾部结点（非空结点）相同，那么就是相交的。避免了两个链表根本不相交但依然要去执行上述逻辑，这样的无用功，算是进行了优化。还可以优化的细节，如果其中一个链表为空，那么他们就没有相交结点，直接返回一个空结点即可。代码实现如下：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    if(headA == NULL || headB == NULL)
    return NULL;

    //1.获取两链表的差距步数
    int lenA = 1, lenB = 1;
    struct ListNode* tailA = headA, *tailB = headB;
    //1.1 获取A链表的长度
    while(tailA->next)
    {
        tailA = tailA->next;
        lenA++;
    }
    //1.2 获取B链表的长度
    while(tailB->next)
    {
        tailB = tailB->next;
        lenB++;
    }
    //如果两个链表根本不相交，就不要做无用功
    if(tailA != tailB)
    {
        return NULL;
    }
    int gap = abs(lenA - lenB);
    struct ListNode* longList = headA;
    struct ListNode* shortList = headB;
    if(lenA < lenB)
    {
        longList = headB;
        shortList = headA;
    }
    //2.长的链表先走差距步
    while(gap--)
    {
        longList = longList->next;
    }

    //3.短的链表从头开始，一起走
    while(longList)
    {
        //遇到相等的结点了，该结点就是相交结点
        if(longList == shortList)
        {
            return longList;
        }
        longList = longList->next;
        shortList = shortList->next;
    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

判断链表中是否存在环

给你一个链表的头节点 head ，判断链表中是否有环。例如：

点击此处前往该类题， 为了方便描述这类问题，我们给出更为抽象一点的逻辑图

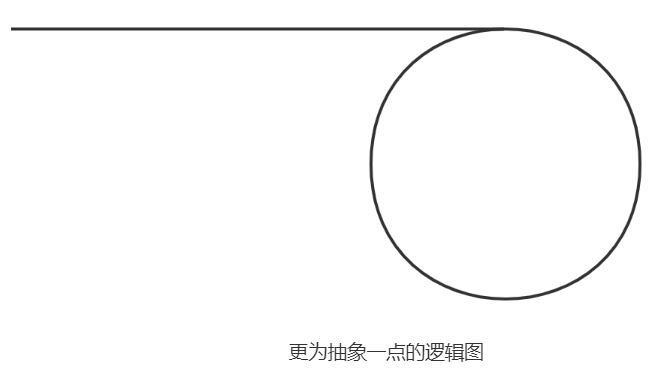
判断一个链表中存在环，更为普遍的办法是定义两个指针，一个指针一次走一步，另一指针一次走两步，前者我们称之为慢指针，后者称之为快指针。若存在环，那么快指针必定会追上慢指针；若不存在环，快指针必定会先走到链表尾部。

为什么慢指针一次走一步，快指针一次走两步，若存在环，快指针必定会追上慢指针的原理证明：
若存在环，当slow开始进环时，fast已经在环里面了。假设入环前的长度为L，那么当slow开始进环时，fast已经在环内走了L（slow走了L，fast就走了2L，fast入环前已经走了L，故在环内走了L）。下面的这张示意图，是环比入环前距离大的样例。也有可能slow进环前，fast已经在环里走了好几圈了！但要记住无论环大还是环小，fast在环内走了几圈，fast在环内所走的步数一定是L。

fast去追slow，slow开始进环时，假设它们之间的距离为N，要分清楚这里所指的距离到底是哪一段。
走一次：slow走了一步，fast走了两步。那么slow和fast之间的距离就减少了1，此时距离为N-1
走一次：slow走了一步，fast走了两步。那么slow和fast之间的距离就减少了1，此时距离为N-2
走一次：slow走了一步，fast走了两步。那么slow和fast之间的距离就减少了1，此时距离为N-3
… …
slow在环内走了N次后：此时距离为N-N = 0，fast追上了slow!

到这里的时候，你可能会产生疑问，为什么一定是慢指针一次走一步，快指针一次走两步。快指针一次走三步行不行？一起验证这样的假设是否可行。

不管fast在环内走了多少，假设slow开始进环时，fast和slow相距N

走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为N-2
走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为N-4
走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为N-6
… …

如果N是偶数，也就是slow开始进环时，两指针的差距是偶数，距离才会逐渐变为0；否则就有可能会错过

• 以slow开始进环时，slow和fast距离N为偶数6举例：
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为4
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为2
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为0
  fast追上slow了，该链表存在环！

• 以slow开始进环时，slow和fast距离N为奇数7举例：
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为5
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为3
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为1
  走一次：slow走了一步，fast走了三步。那么slow和fast之间的距离就减少了2，此时距离为-1
  距离变成了-1？实质上，两者的距离又开始反向变大了！这一次就错过了
  
  当然，还可以让fast继续追slow,这一轮是否会错过，要取决于环的大小，这不就是上一步操作的轮询吗？C为环的大小，此时C-1就是两者之间的距离差N。如果C-1为偶数，那么fast就可以追上slow，从而证明该链表存在环；如果C-1依旧为奇数，那么就会永远错过，无法证明该链表是否存在环。

其他方案请自行证明。 综合而言，慢指针一次走一步、快指针一次走两步是判断链表中是否存在环的最优解决方案。参考代码如下：

bool hasCycle(struct ListNode *head) {
	//如果链表为空，一定不存在环
    if(head == NULL)
    {
        return false;
    }
    struct ListNode* slow = head, *fast = head;
    while(fast && fast->next)
    {
    	//慢指针一次走一步
    	//快指针一次走两步
        slow = slow->next;
        fast = fast->next->next;
        if(fast == slow)
        {
            return true;
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

链表中环的入口结点

经过前两个类型的题，算是为这道题打下一些基础知识，
题目：给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

思考“判断链表存在环”类题，并结合其中的两个图，你能联想到什么？
环比入环前长度大的情况：

入环前的长度、相遇点到入环结点的长度都是L。到这里我们就应该能想到两个链表相交的思想，如果你看不出来，我们可以将其中部分稍微拉平一点。

再使用“找相交链表的第一个相交结点”的办法，就能够找到找到这个入环结点了。

当然，这是环大小比入环前长度大的情况。环比较小的情况也是一样的，由于采用慢指针一次走一步、快指针一次走两步的策略，慢指针slow开始入环前，快指针fast已经在环内走了L步（不管它究竟在环内走了几圈）。所以环比较小时，fast走过几圈了的长度+快慢指针相遇点到入环结点的长度 = L。
绕过一个弯来说，不论环大还是环小，我们都只需要定义两个指针，一个指针从链表的头部开始走，一个指针从快慢指针相遇点走，都是一次走一步。如果有环，那么它们必定会相遇。相遇的点，便是入环结点
（1）环比较大时，快慢指针相遇点开始走的指针，不会走超过环的一圈。
（2）环比较小时，快慢指针相遇点开始走的指针，会走了环的很多圈。

综上所述，我们可以总结出求解入环结点的思路：
（1）判断链表中是否存在环，同时得到其中快慢指针相遇的结点；
（2）定义两个指针，一个指针从链表头部开始走，另一指针从快慢指针相遇点开始走；
（3）两个指针相遇的结点，就是入环结点。

//判断是否存在环，并且得到快慢指针相遇的结点
struct ListNode* hasCycle(struct ListNode* head){
    if(head == NULL)
    return NULL;

    struct ListNode *slow = head, *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        //fast追上了slow,存在环
        if(slow == fast)
        {
            return fast;
        }
    }
    return NULL;
}
struct ListNode *detectCycle(struct ListNode *head) {
    //判断是否存在环，如果存在则获得快慢指针相遇点
    struct ListNode* meetNode = hasCycle(head);
    if(meetNode == NULL)
    {
        //不存在环
        return NULL;
    }

    //另外定义两个指针
    //一个指针从链表头开始走，一个指针从快慢指针相遇点开始走
    struct ListNode* ptr1 = head, *ptr2 = meetNode;
    while(ptr1 != ptr2)
    {
        ptr1 = ptr1->next;
        ptr2 = ptr2->next;
        //两个指针相遇了，相遇结点便是入环结点
        if(ptr1 == ptr2)
        {
            return ptr1;
        }
    }
    //如果能够到这里，说明第一个结点就是入环结点
    return head;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43