【HDU No. 5057】序列操作 Argestes and Sequence

【HDU No. 5057】序列操作 Argestes and Sequence

杭电OJ 题目地址

【题意】

有由N 个非负整数组成的序列：a [1],a [2], …, a [N ]，对该序列进行M 个操作，操作形式：①S X Y ，将a [X ]的值设置为Y （a [X ]=Y ）；②Q L R D P ，求[L , R ]区间第D 位是P 的元素个数，L 和R 是序列的索引。

注意：第1位是最低有效位。

【输入输出】

输入：

第1行包含一个整数T ，表示测试用例的数量。每个测试用例的第1行都包含两个整数N 和M 。第2行包含N 个整数：a [1], a[2], …, a [N ]。接下来的M 行操作，若类型为S，则在该行中将包含两个整数X、Y ；若类型为Q，则将包含4个整数L、R、D、P 。

其中：1≤T ≤50，1≤N , M ≤105 ，0≤a [i ]≤231 -1，1≤X ≤N ，0≤Y≤231 -1，1≤L ≤R ≤N ，1≤D ≤10，0≤P ≤9。

输出：

对每个Q操作，都单行输出答案。

【样例】

【思路分析】

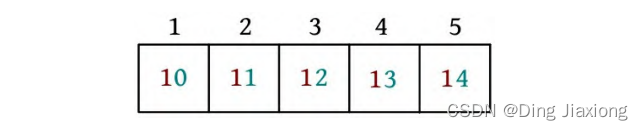
根据测试用例的输入数据，序列如下图所示。

• Q 1 5 2 1：查询到[1, 5]区间第2位是1的元素有5个。

• Q 1 5 1 0：查询到[1, 5]区间第1位是0的元素有1个。

• Q 1 5 1 1：查询到[1, 5]区间第1位是1的元素有1个。

• Q 1 5 3 0：查询到[1, 5]区间第3位是0的元素有5个。

• Q 1 5 3 1：查询到[1, 5]区间第3位是1的元素有0个。

• S 1 100：将第1个元素修改为100。
  

• Q 1 5 3 1：查询到[1, 5]区间第3位是1的元素有1个。

这道题包括点更新和区间查询，区间查询比较特殊，需要查询第D 位是P 的元素个数，可以采用分块的方法来解决。

【算法设计】

① 分块。划分块，统计每一块每一位上的元素个数。block[i ][j ][k ]表示第i 块中第j 位是k 的元素个数。

② 查询。查询[l , r ]区间第d 位是p 的元素个数。

• 若该区间属于同一块，则暴力累加块内第d 位是p 的元素个数。
• 若该区间包含多个块，则累加中间每一块i 的block[i ][d ][p]，然后暴力累加左端和右端第d 位是p 的元素个数。

③ 更新。将a [x ]的值更新为y 。因为原来x 所属的块已统计了a [x ]每一位上的元素个数，所以此时需要减去，再将新的值y 累加上即可。

【算法实现】

#include
#include
#include
#include

using namespace std;
#define maxn 100010
int a[maxn],belong[maxn],L[maxn],R[maxn],block[400][12][12],n,m;

//block[i][j][k]表示第i块中第j位上是k的数有多少个
int ten[11]={0,1,10,100,1000,10000,100000,1000000,10000000,100000000,1000000000};

void build(){
    int t=sqrt(n);
    int num=n/t;
    if(n%t)  num++;
    for(int i=1;i<=num;i++){
        L[i]=(i-1)*t+1;//每块的左右 
        R[i]=i*t;
    }
    R[num]=n;
    for(int i=1;i<=n;i++)
		belong[i]=(i-1)/t+1;//所属块 
    for(int i=1;i<=n;i++){
        int temp=a[i];
        for(int j=1;j<=10;j++){//位数最多有10位1<=D<=10
            block[belong[i]][j][temp%10]++;//块，位，位上的数 
            temp/=10;
        }
    }
}

int query(int l,int r,int d,int p){
    int ans=0;
    if(belong[l]==belong[r]){//属于同一块
        for(int i=l;i<=r;i++)//暴力统计 
            if((a[i]/ten[d])%10==p)
				ans++;
        return ans;
    }
    for(int i=belong[l]+1;i<belong[r];i++)//累加中间块 
		ans+=block[i][d][p];
    for(int i=l;i<=R[belong[l]];i++){//左端暴力累加 
        if((a[i]/ten[d])%10==p)
			ans++;
    }
    for(int i=L[belong[r]];i<=r;i++){//右端暴力累加
        if((a[i]/ten[d])%10==p)
			ans++;
    }
    return ans;
}

void update(int x,int y){
    for(int i=1;i<=10;i++){//原来的统计数减少 
        block[belong[x]][i][a[x]%10]--;
        a[x]/=10;
    }
    a[x]=y;
    for(int i=1;i<=10;i++){//新的统计数增加 
        block[belong[x]][i][y%10]++;
        y/=10;
    }
}

int main(){
	
    int T;
    scanf("%d",&T);
    while(T--){
        memset(block,0,sizeof(block));
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
			scanf("%d",&a[i]);
        build();//划分块 
        char s[5];
        while(m--){
            scanf("%s",s);
            if(s[0]=='S'){
                int x,y;
                scanf("%d%d",&x,&y);
                update(x,y);
            }
            else{
                int l,r,d,p;
                scanf("%d%d%d%d",&l,&r,&d,&p);
                printf("%d\n",query(l,r,d,p));
            }
        }
    }
	
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94