第十四章 图的存储及图的DFS（超级详细！！逐行解析！！）

一、图

1、什么是图？

下面这种结构就是图：

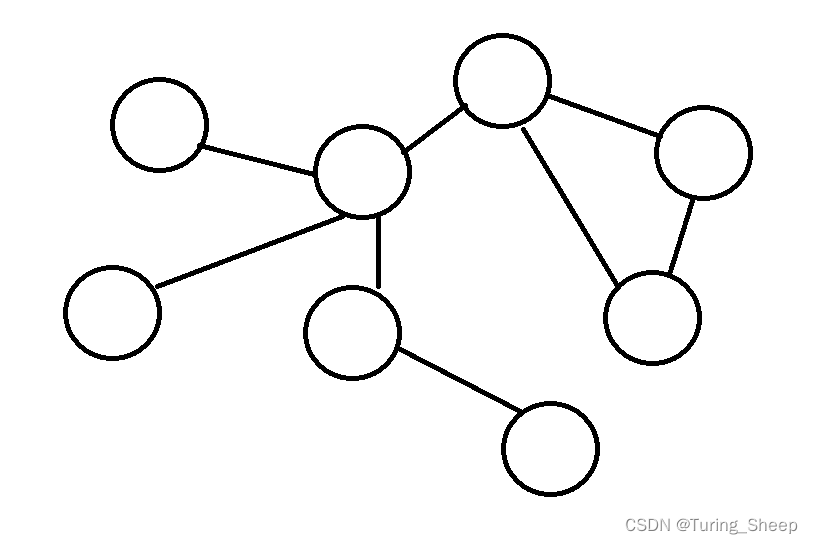
图包含了两个基本元素：顶点（vertex, 简称V）和边（edge,简称E）。看到这个结构我们第一个想到的就是，图和树的结构是很类似的。没错，树是一种特殊的图，树是有向无环图。那么从这个概念出发，我们就能得到图的分类标准：有环无环，有向无向。
环很好理解，看图就能够看出来。那么什么叫有向和无向呢？
我们刚才上面介绍的那个图就是无向的，而下图就是有向的。

那么有向和无向有什么影响呢？

在对图有了一个基本的了解后，我们应该如何存储一个图呢？

2、图的存储

（1）邻接矩阵

图的组成要素是点和边。

点的存储是很好解决的，我们用int,char等数据类型的变量来表示点就好。而边的话，其实说白了，边就是两个点之间的关系。而我们需要存储的其实就是这种关系。

因此，我们可以创建一个二维数组。例如a[1][2]=1。就表示从1到2有一条有向边。a[2][1]=0则表示，从2到1没有一条边。因此，我们就构建好了一个从1到2的有向边。那么假设我们让a[2][1]也等于1。
那么2和1之间就存在一个双向边，也就是我们刚才介绍的无向边的等效情况。

那么以上通过两个点作为下标，将边存储在一个二维数组中的存储方式就称之为邻接矩阵。

但是这种方式有一个很大的问题，就是其浪费的空间非常多！！！！所以效果是很低效的，那么为了解决这个方法，我们采用下图中的邻接表的方式存储图。

（2）邻接表

邻接表其实全名应该叫做：邻接链表
顾名思义就是我们利用链表来存储图，其结构类似于我们之前学的哈希表。

上图中：左侧的数组存储的是图中的所有点。

链表中存储的是图中的所有边！这里一定要记住！！！链表中的点存储的是边！边！边！
有一个节点就是有一个边，节点中的内容是该边的终点。

我们将上述的邻接表的部分内容转为图的话，如下图所示：

二、图的深度优先搜索

1、思路

其实图中的深度优先搜索和之前的思路是一致的，就是一路走到黑。碰壁之后，就回溯，然后再走到黑。

2、模板

（1）问题：

分析

我们删除图中的节点B。会得到如下的结果：

删除B后，我们剩下的是B点的左子树、右子树、以及除了除了以B为根节点的树的剩余部分。
那么在这三部分中，节点最多的部分中的节点数量为：4 。那么我们需要去掉每个节点，然后都求出这样一个最大值，之后在这些最大值中挑出一个最小值输出。

那么这道题其实就可以转化成：求出每个节点的左右子树即可。为什么呢？因为第三部分其实就是整体减去B点再减去左右子树。因此，只需要求出左右子树就能计算出结果。

如何求左右子树呢?

我们假设想求A点的左右子树的大小，我们惊奇地发现，它的路线就是一个DFS。但是有人会疑惑：
这不只求了A点的左右子树吗？但是我们看，在求A点左右子树的过程中，我们已经求完了B点的左右子树和C的左右子树。因此，我们只需要去DFS即可。

什么时候记录呢？

当搜索路线再次回来的时候，就是我们记录的时候。 我们发现，当路线第一次回到B的时候，就遍历完了B的左子树。第二次回到B的时候，就遍历完了右子树。当第一次回到A的时候，就遍历完了A的左子树……

如何构造递归函数呢？

递归其实就是分治。因此我们只需要将一个过程中的重复执行的过程抽离出来。

因此重复部分就是我们的函数作用：

所以我们的dfs函数的作用就是求子树数量。

那么上述表达式中的：子树+1就是递归函数的返回值

（2）代码模板：

#include
#include
using namespace std;
const int N=1e5+10;
const int M=3e5+10;
int h[N],e[M],ne[M],idx;
int n,ans=0x3f3f3f3f;
bool m[N];

void add(int x,int y)
{
    e[idx]=y;
    ne[idx]=h[x];
    h[x]=idx++;
}

int dfs(int u)
{
    int sum=0;int s=0,ma=0;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!m[j])
        {
            m[j]=true;
            s=dfs(j);
            sum+=s;
            ma=max(s,ma);
        }
    }
    ma=max(ma,n-sum-1);
    ans=min(ans,ma);
    
    return sum+1;
}

int main()
{
    memset(h,-1,sizeof h);
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int x,y;
        cin>>x>>y;
        add(x,y);
        add(y,x);
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

（3）代码分析: