网络1323的分类行为

( A, B )---2*30*2---( 1, 0 )( 0, 1 )

用网络分类A和B，让A是（0，1）（1，1），让B是（1，0）（1，1）。测试集为（0，0）（0，1）（1，0）（1，1）.记为网络1323.固定收敛误差统计迭代次数和分类准确率，得到表格

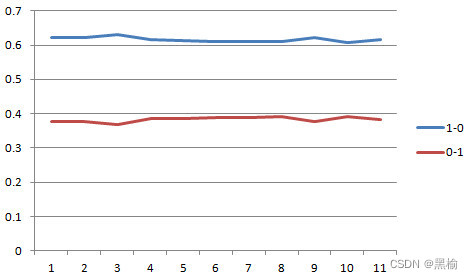
两个位的分类准确率趋于稳定。统计当收敛误差为8e-5时的分类情况

有100次13被分类为A，02被分为B。4次01被分为A，23被分为B。94次013被分为A，2被分为B。1次1被分为A，023被分为B。

（0，0）和A，B两列的相似度都为0，50%，被分为A和B的概率应该是一致的，（0，0）有98次被分为A，有101次被分为B。二者比例接近1：1，这符合假设。

（1，1）和A，B两列的相似性也都是100%，50%。似乎被分为A和B的概率也应该是一致的。但（1，1）有194次被分为A，有5次被分为B。也就是（1，1）几乎全部被分给了A。

所以按照（0，0）对半分，（1，1）按照时序，先到全得的原则，这个网络的极限分类准确率应该是

PA=0.125+0.25+0.25=0.625

PB=0.25+0.125=0.375

做第二个网络，让A和B调换先后顺序，测试集不变再统计分类准确率和迭代次数，得到表格

有100次23被分类为A，01被分为B。1次2被分为A，013被分为B。89次023被分为A，1被分为B。9次02被分为A，13被分为B。

00	98	101
11	189	10

因此有98次(0,0)被分为A，101次被分为B。（1，1）有189次被分为A，10次被分为B。（0，0）被对半分，（1，1）按照时序先到的全得，与假设一致。

与网络2010相比

00	161		38			4.2368
11	94		105			0.8952

这个网络中（1，1）的两列相似度是50%，0.而（1，1）没有时序优先现象，是对半分的。这个与网络1323的（0，0）相同，在1323中（0，0）的相似性也是50%，0.也被对半分。

而在网络2010中（0，0）的两列相似性为50%，100%，就存在时序现象。这和网络1323中的（1，1）一致，（1，1）在1323中的两列相似性也是50%，100%就存在时序现象。但区别是2010的（0，0）被按照4：1的比例分割，而1323中的（1，1）按照1：0的比例分割。