代码随想录训练营第39天|LeetCode 62.不同路径、63. 不同路径 II

参考

代码随想录

题目一：LeetCode 62.不同路径

相比于之前的爬楼梯，这题变成了二维，对于某个位置[i,j]，可以从[i-1,j]或者[i,j-1]走到[i,j]，因此在求解思想上其实是类似于爬楼梯的。

1. 确定dp数组及其下标的含义
   dp[i][j]为从[0,0]位置走到[i,j]位置的路径数
2. 确定递归公式
   每次可以选择往右或往下走，当前在边界处除外，因此每个位置有两种方式到达,递推公式为

dp[i][j] = dp[i-1][j] + dp[i][j-1]
1

3. 初始化dp数组
   需要初始化第一行和第一列，一方面是因为第一行和第一列的dp数组的值是确定的，都为1（因为在第一行，每次只能往右走，在第一列，每次只能往下走），另一方面，后面的dp数组需要由前面的数值推出来。初始化代码如下：

for(int i = 0; i < m; i++)  dp[i][0] = 1;
for(int i = 0; i < n; i++)  dp[0][i] = 1;
1
2

4. 确定遍历顺序
   对于每一行，从左往右遍历；对于每一列，从上往下遍历。先遍历行还是先遍历列都可以，遍历顺序是由递推公式来决定的，dp[i][j]要由dp[i-][j]和dp[i][j-1]推出来。
5. 举例推导dp数组
   
   整体的代码实现如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m,vector<int>((n)));
        for(int i = 0; i < m; i++)  dp[i][0] = 1;
        for(int i = 0; i < n; i++)  dp[0][i] = 1;
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];       
            }
        }
        return dp[m-1][n-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

题目二：LeetCode 63.不同路径II

这个题在上一个题的基础之上加入了障碍物，如下图，因为障碍物的存在，图中红色方框标记的两个地方只能由一个方向过来。思路上没有问题，但是这样在代码实现上稍微有些复杂，换个思路，只要把障碍物所在的地方的dp数组的值标记为0就可以了，这里的dp数组的含义与上一个题一致。

1. 确定dp数组及其下标的含义
   dp[i][j]为从[0,0]位置走到[i,j]位置的路径数
2. 确定递归公式
   每次可以选择往右或往下走，当前在边界处除外，因此每个位置有两种方式到达,递推公式为

dp[i][j] = dp[i-1][j] + dp[i][j-1]
1

3. 初始化dp数组
   dp数组的初始化要注意，如果第一行或第一列的某个位置出现障碍物，则后面的都应该初始化为0，如下图所示：
   
   

for(int i = 0; i < m && !obstacleGrid[i][0]; i++) dp[i][0] = 1;
for(int j = 0; j < n && !obstacleGrid[0][j]; j++) dp[0][j] = 1;
1
2

4. 确定遍历顺序
   对于每一行，从左往右遍历；对于每一列，从上往下遍历。先遍历行还是先遍历列都可以，遍历顺序是由递推公式来决定的，dp[i][j]要由dp[i-][j]和dp[i][j-1]推出来。

5.举例推导dp数组


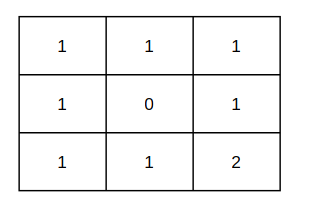
完整的代码实现如下：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m,vector<int>((n)));
        for(int i = 0; i < m && !obstacleGrid[i][0]; i++) dp[i][0] = 1;
        for(int j = 0; j < n && !obstacleGrid[0][j]; j++) dp[0][j] = 1;
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(obstacleGrid[i][j]) 
                    dp[i][j] = 0;
                else   
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];       
            }
        }
        return dp[m-1][n-1];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19