Polygon zkEVM R1CS与Plonk电路转换

1. 引言

前序博客有：

• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• rank-1 constraint system R1CS

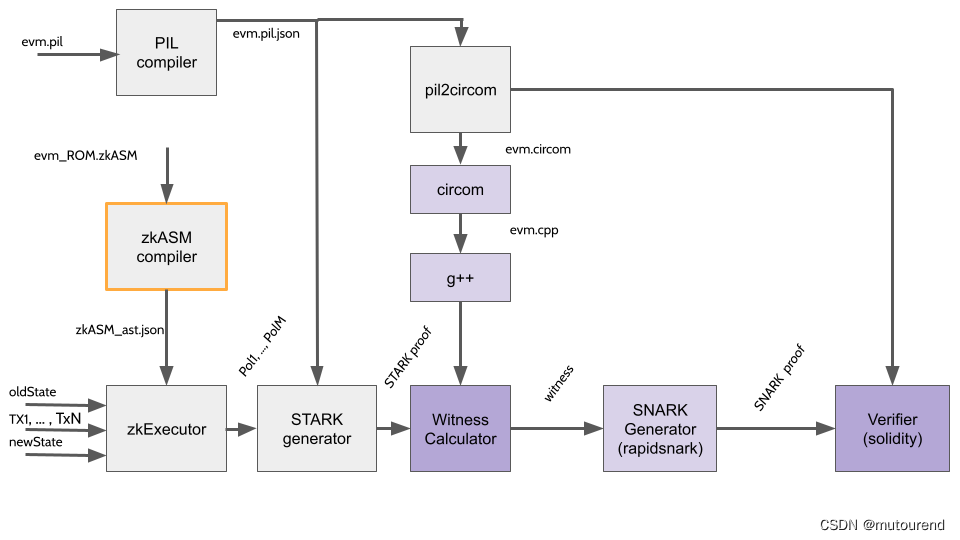
由上图可知，zkEVM会借助SNARK来“验证（（验证STARK证明）的SNARK证明）”：

• 1）将 STARK proof的约束系统evm.pil 经 pil2circom 转换为 evm.verifier.cricom格式。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第8步“fibonacci generate circom”。
• 2）再借助 circom工具 将 STARK约束系统 转换为 R1CS约束系统表示evm.verifier.r1cs。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第9步“”
• 3）再经 Compressor12_setup 将 R1CS约束系统表示evm.verifier.r1cs 转换为 Plonk约束表示，同时会生成与 Plonk约束表示 对应的 STARK约束evm.c12.pil，以及 constant多项式的execution trace evm.c12.const 和 Plonk辅助信息 evm.c12.exec。详细见 Polygon zkEVM的pil-stark Fibonacci状态机初体验 第2节第10步“fibonacci C12 setup”。Plonk辅助信息 evm.c12.exec 会用于后续生成 commit多项式execution trace evm.c12.commit。

2. 约束表达

约束表达：

• 1）STARK：采用execution trace来表示约束，以表格形式来表示内部程序状态的变化。如：

  序号	$x$	$\mathbf{A}$（$l_2(x)$多项式）	$\mathbf{B}$（$l_1(x)$多项式）	$\mathbf{i}\mathbf{s}\mathbf{I}\mathbf{n}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{a}\mathbf{l}$（$L_1(x)$多项式）	$\mathbf{i}\mathbf{s}\mathbf{L}\mathbf{a}\mathbf{s}\mathbf{t}$（$LLAST(x)$多项式）
  0	${\omega }^0$	1	2	1	0
  1	${\omega }^1$	2	5	0	0
  2	${\omega }^2$	5	29	0	0
  $⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
  1023	${\omega }^{1023}$	…	74469561660084004	0	1

• 2）Groth16等SNARK方案：采用R1CS来表示约束，形如$<\vec{s},\vec{a}>\ast <\vec{s},\vec{b}>-<\vec{s},\vec{c}>=0$，其中$<\vec{s},\vec{a}>={\sum }_{i=1}^n{s}_i{a}_i$为dot product，$\vec{a},\vec{b},\vec{c}$为每步计算的系数，$\vec{s}$为相应的输入。
• 3）Halo2等SNARK方案：采用Plonk来表示约束，形如$Q_m\ast x_r\ast x_l+Q_l\ast x_l+Q_r\ast x_r+Q_o\ast x_o+Q_k=0$，其中$Q_m,Q_l,Q_r,Q_o,Q_k$均为selector，$x_l,x_r,x_o$为相应的输入。

以PIL-STARK 中的Fibonacci为例，在验证其STARK proof的Plonk表达中，除以上$Q_m,Q_l,Q_r,Q_o,Q_k$ selector之外，还额外引入了定制门 selector $Q_{MDS},Q_{CMUL}$：

pol constant Qm, Ql, Qr, Qo, Qk, QMDS, QCMul; //selector
1

fibonacci.c12.pil约束中的execution trace输入每行有12个：

pol commit a[12]; // 输入寄存器，粒度为单个Goldilocks基域元素
1

公开输入的约束为：

	public pub0 = a[0](0); //公开输入，对应Goldilocks基域
    public pub1 = a[1](0);
    public pub2 = a[2](0);
    Global.L1 * (a[0] - :pub0) = 0; //L1为常量多项式
    Global.L1 * (a[1] - :pub1) = 0;
    Global.L1 * (a[2] - :pub2) = 0;
1
2
3
4
5
6

对于常规Plonk equation来说，execution trace中每一行的12个输入，每3个输入对应一个Plonk约束，一行对应4个Plonk约束：

// Normal plonk equations //标准Plonk 电路，一行有4个Plonk 标准电路
    pol a01 = a[0]*a[1];
    Qm*a01 + Ql*a[0] + Qr*a[1] + Qo*a[2] + Qk = 0;

    pol a34 = a[3]*a[4];
    Qm*a34 + Ql*a[3] + Qr*a[4] + Qo*a[5] + Qk = 0;

    pol a67 = a[6]*a[7];
    Qm*a67 + Ql*a[6] + Qr*a[7] + Qo*a[8] +Qk = 0;

    pol a910 = a[9]*a[10];
    Qm*a910 + Ql*a[9] + Qr*a[10] + Qo*a[11] +Qk = 0;
1
2
3
4
5
6
7
8
9
10
11
12

对于MDS定制电路，execution trace下一行与上一行值的约束关系为：【MDS定制电路，需使用execution trace中的2行输入】

// MDS 定制电路，一个电路占用两行

    QMDS * (a[ 0]' - (25*a[0] + 15*a[1] + 41*a[2] + 16*a[3] +  2*a[4] + 28*a[5] + 13*a[6] + 13*a[7] + 39*a[8] + 18*a[9] + 34*a[10] + 20*a[11])) = 0;
    QMDS * (a[ 1]' - (20*a[0] + 17*a[1] + 15*a[2] + 41*a[3] + 16*a[4] +  2*a[5] + 28*a[6] + 13*a[7] + 13*a[8] + 39*a[9] + 18*a[10] + 34*a[11])) = 0;
    QMDS * (a[ 2]' - (34*a[0] + 20*a[1] + 17*a[2] + 15*a[3] + 41*a[4] + 16*a[5] +  2*a[6] + 28*a[7] + 13*a[8] + 13*a[9] + 39*a[10] + 18*a[11])) = 0;
    QMDS * (a[ 3]' - (18*a[0] + 34*a[1] + 20*a[2] + 17*a[3] + 15*a[4] + 41*a[5] + 16*a[6] +  2*a[7] + 28*a[8] + 13*a[9] + 13*a[10] + 39*a[11])) = 0;
    QMDS * (a[ 4]' - (39*a[0] + 18*a[1] + 34*a[2] + 20*a[3] + 17*a[4] + 15*a[5] + 41*a[6] + 16*a[7] +  2*a[8] + 28*a[9] + 13*a[10] + 13*a[11])) = 0;
    QMDS * (a[ 5]' - (13*a[0] + 39*a[1] + 18*a[2] + 34*a[3] + 20*a[4] + 17*a[5] + 15*a[6] + 41*a[7] + 16*a[8] +  2*a[9] + 28*a[10] + 13*a[11])) = 0;
    QMDS * (a[ 6]' - (13*a[0] + 13*a[1] + 39*a[2] + 18*a[3] + 34*a[4] + 20*a[5] + 17*a[6] + 15*a[7] + 41*a[8] + 16*a[9] +  2*a[10] + 28*a[11])) = 0;
    QMDS * (a[ 7]' - (28*a[0] + 13*a[1] + 13*a[2] + 39*a[3] + 18*a[4] + 34*a[5] + 20*a[6] + 17*a[7] + 15*a[8] + 41*a[9] + 16*a[10] +  2*a[11])) = 0;
    QMDS * (a[ 8]' - ( 2*a[0] + 28*a[1] + 13*a[2] + 13*a[3] + 39*a[4] + 18*a[5] + 34*a[6] + 20*a[7] + 17*a[8] + 15*a[9] + 41*a[10] + 16*a[11])) = 0;
    QMDS * (a[ 9]' - (16*a[0] +  2*a[1] + 28*a[2] + 13*a[3] + 13*a[4] + 39*a[5] + 18*a[6] + 34*a[7] + 20*a[8] + 17*a[9] + 15*a[10] + 41*a[11])) = 0;
    QMDS * (a[10]' - (41*a[0] + 16*a[1] +  2*a[2] + 28*a[3] + 13*a[4] + 13*a[5] + 39*a[6] + 18*a[7] + 34*a[8] + 20*a[9] + 17*a[10] + 15*a[11])) = 0;
    QMDS * (a[11]' - (15*a[0] + 41*a[1] + 16*a[2] +  2*a[3] + 28*a[4] + 13*a[5] + 13*a[6] + 39*a[7] + 18*a[8] + 34*a[9] + 20*a[10] + 17*a[11])) = 0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

Goldilocks extension 3域乘法运算逻辑为：

mul(a, b) {
        if (typeof(a) == "bigint") { //a为整数，Goldilocks基域
            if (typeof(b) == "bigint") { //b为整数，Goldilocks基域
                return (a*b) % this.p;
            } else { //b为Goldilocks extension 3域
                return [(a*b[0]) % this.p,  (a*b[1]) % this.p, (a*b[2]) % this.p];
            }
        } else if (typeof(b) == "bigint") { //b为整数，Goldilocks基域
            return [(a[0]*b) % this.p,  (a[1]*b) % this.p, (a[2]*b) % this.p];
        } else { //a和b均为Goldilocks extension 3域
            const A = (a[0] + a[1])  * (b[0] + b[1]);
            const B = (a[0] + a[2])  * (b[0] + b[2]);
            const C = (a[1] + a[2])  * (b[1] + b[2]);
            const D = a[0]*b[0];
            const E = a[1]*b[1];
            const F = a[2]*b[2];
            const G = D - E;

            return [ (C + G - F)%this.p,  (A + C - E -E - D )%this.p,(B-G)%this.p ];
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

当a和b均为Goldilocks extension 3域时，计算$c=a\ast b$的约束表示为，将execution trace一行中的前3个输入表示为$a$，接下来3个输入表示为$b$，再接下来的3个输入表示为$c$：

// CMUL // mul 乘法定制电路，一个占用一行

    pol A = (a[0] + a[1])  * (a[3] + a[4]);
    pol B = (a[0] + a[2])  * (a[3] + a[5]);
    pol C = (a[1] + a[2])  * (a[4] + a[5]);
    pol D = a[0]*a[3];
    pol E = a[1]*a[4];
    pol F = a[2]*a[5];

    QCMul * (a[6] - (C + D - E - F)) = 0;
    QCMul * (a[7] - (A + C - 2*E - D)) = 0;
    QCMul * (a[8] - (B - D + E)) = 0;
1
2
3
4
5
6
7
8
9
10
11
12

为了表示execution trace中各元素之间的copy constraints关系，引入了：

	pol constant S[12]; // 用于copy constraints
	
// Connection equations
    {a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8], a[9], a[10], a[11]} connect
        {S[0], S[1], S[2], S[3], S[4], S[5], S[6], S[7], S[8], S[9], S[10], S[11]};
1
2
3
4
5

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理
• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束
• Polygon zkEVM Merkle tree的circom约束
• Polygon zkEVM FFT和多项式evaluate计算的circom约束