【数据可视化】Data Reduction和加利福尼亚的房价数据集数据可视化以及Kettle的初步介绍

一.数据归约Data Reduction

• 对海量数据进行复杂的数据分析和机器学习将需要很长时间，使得这种分析不现实或不可行。
• 数据归约技术可以用来得到数据集的归约表示，它小得多，但仍接近保持原数据的完整性。
• 对归约后的数据集计算将更有效，并产生相同（或几乎相同）的结果。

1.1数据归约

数据归约策略： (1)数据立方聚集：对数据立方做聚集操作

(2)维度归约：删除不重要的属性

(3)数值归约： 一用规模较小的数据表示、替换或估计原始数据

(4)数据压缩 (5)离散化和概念分层(concept hierarchy)-属性的原始数值用区间值或较高层的概念替换

1.2 概念分层

1.3数据立方体聚集

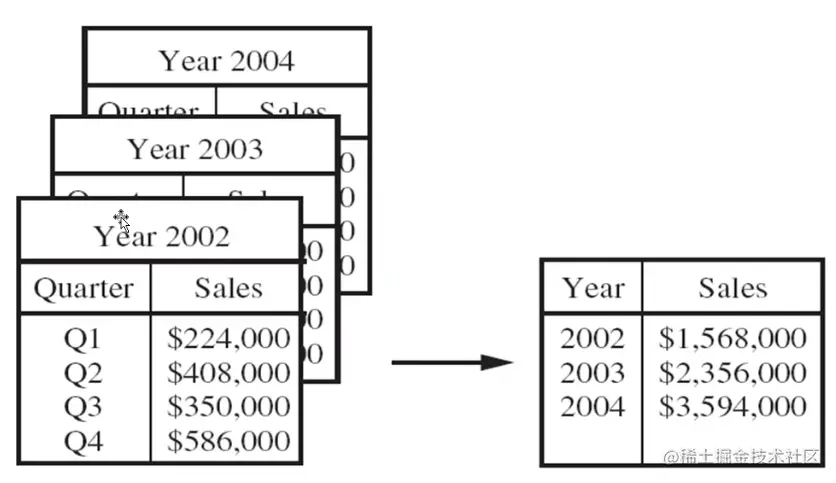
• 数据立方体存储多维聚集信息,提供对预计算的汇总数据进行快速访问。 如:立方体内存储季度销售额,若对年销售额感兴趣,可对数据执行聚集操作,例如sum()等。

  

1.4属性子集选择(维度归约)

• 通过删除不相关或冗余的属性(或维)减小数据集。

• 其目标是找出最小属性集,使得数据类的概率分布尽可能地接近使用所有属性得到的原分布。

• 通过穷举搜索找出有属性的最佳子集是不现实的。通常采用压缩搜索空间的启发式算法。如贪心算法:从局部最优到全局最优。 -逐步向前选择

  -逐步向后删除

  -向前选择和向后删除的结合

  -决策树归纳

1.5维度归约

维度归约使用数据编码或变换，以便得到原数据的归约或““压缩”表示。分为无损和有损两种

• 主要方法：
  • 中-串压缩：无损，但只允许有限的数据操作。
  • 小波变换((DWT) ：有损，适合高维数据。
  • -主成分分析(PC A) ：有损，能更好地处理稀疏数据。

1.6 数值归约

1.通过选择替代的、"较小的"数据表示形式来减少数据量。 2.可以分为参数方法和非参数方法。

• 参数方法:回归(regression)和对数线性模型

• 非参数方法:直方图、聚类、抽样

1.6.1 抽样

用数据的小得多的随机样本（子集）代替大型数据集。

抽样方法：

• s个样本无放回简单随机抽样（SRSWOR）

• s个样本有放回简单随机抽样（SRSWR）

• 聚类抽样

• 分层抽样

二.加利福尼亚的房价数据集数据可视化

采用加利福尼亚的房价数据集，准备工作：

from sklearn.datasets import fetch_california_housing
import pandas as pd
housing = fetch_california_housing()
X = housing.data
y = housing.target
df=pd.DataFrame()
for i in range(8):
    df[housing["feature_names"][i]]=X[:,i]
df["target"]=y
# df.to_csv("fetch_california_housing.csv",index=None)
pd.set_option('display.max_column', None)
df.describe()
复制代码

进行绘图

feature = 1
feature_other = 2
# feature_o=0
plt.figure(figsize=(18,18))
feature_max_num=X.shape[1]
for feature in range(feature_max_num):
    for feature_other in range(feature_max_num):
        plt.subplot(feature_max_num,feature_max_num,feature*feature_max_num+feature_other+1,frame_on=True)
        if feature==feature_other:
            plt.hist(X[:,feature])
        else:
            plt.scatter(X[:,feature], X[:, feature_other], color='green', marker='o',label='class_0')
plt.show()
复制代码

运行截图如下：

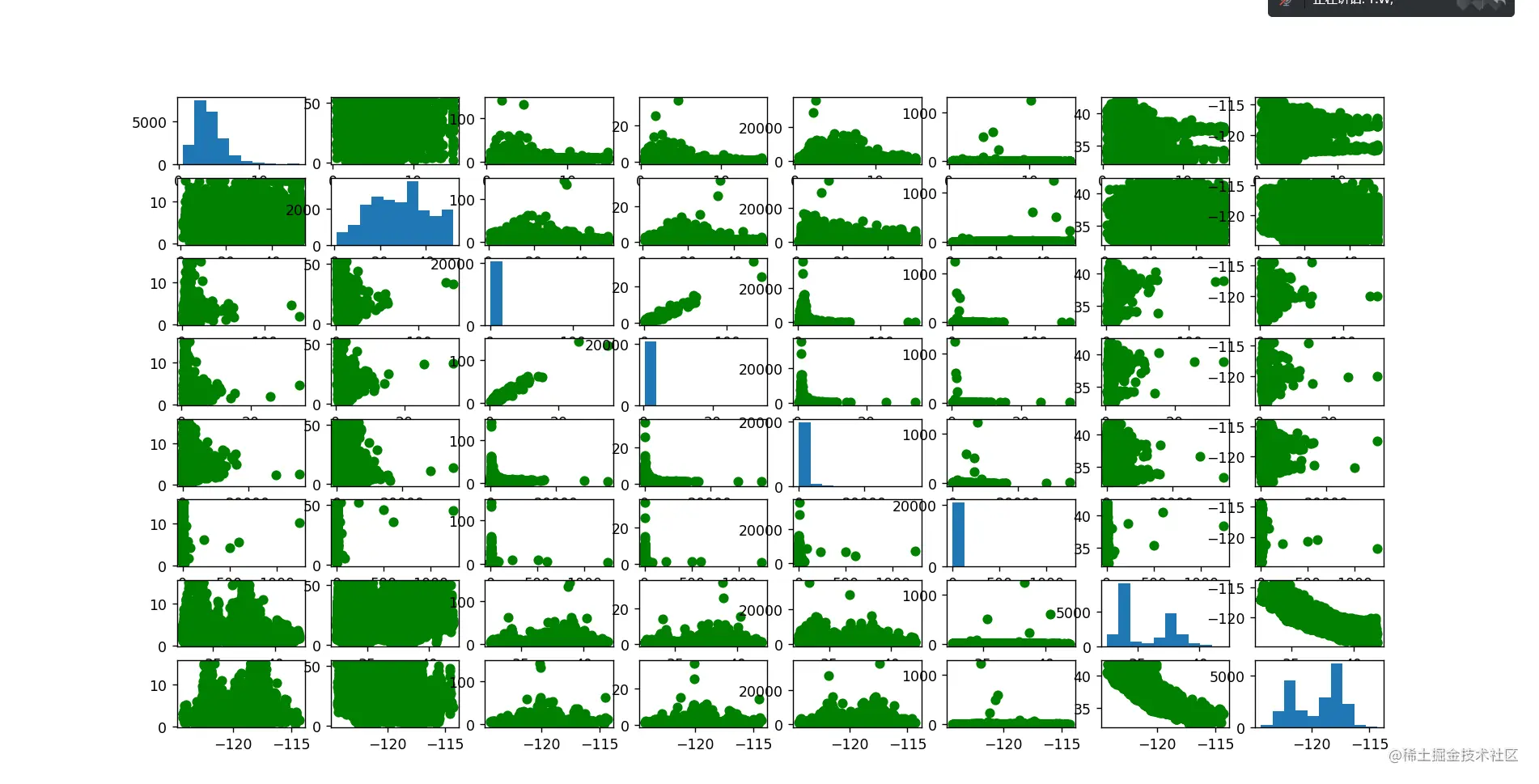
散点图如下

new_subset=df.copy()
 
for col in new_subset.columns:
    if col == "target":
        next
    else:
        new_subset["sqrt_"+col]=np.sqrt(abs(new_subset[col]))
        new_subset["log_" + col] = np.log(abs(new_subset[col]))
 
pd.plotting.scatter_matrix(df,figsize=(18,18))
plt.show()
复制代码

运行结果如下：

热力图：

上面的图只能看出个大概轮廓来， 看不出别的什么信息。我们可以将alpha选项(透明度) 设置成0.1.这样能够区分出高密度数据点的位置

绘制Longitude与Latitude的散点图。alpha设置的越小透明度越低

plt.figure(figsize=(12, 12))
plt.scatter(new_subset['Longitude'], new_subset['Latitude'] , alpha=0.1)
plt.xlabel("Longitude",size=20)
plt.ylabel('Latitude',size=20)
plt.title('Longitude vs Latitude',size=20)
plt.show()
复制代码

运行结果如下：

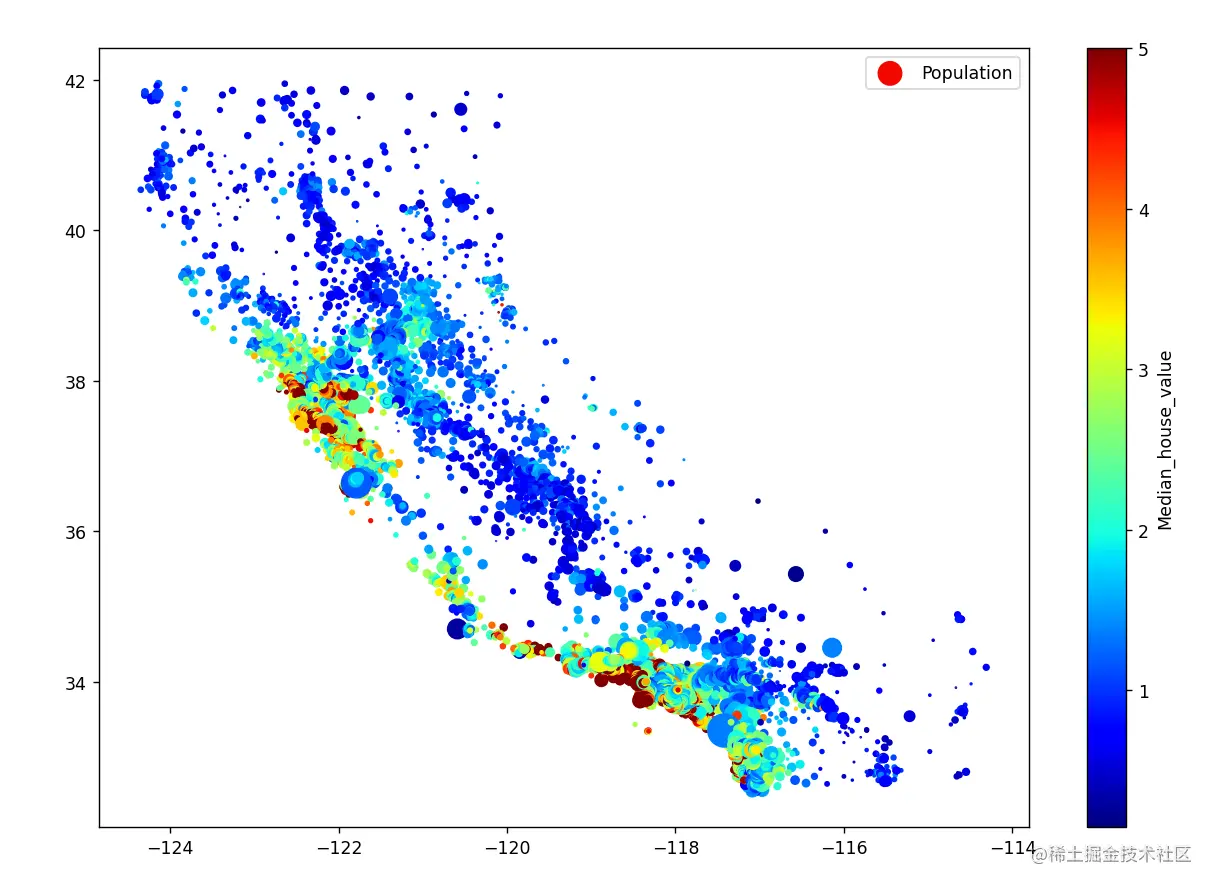
现在可以清楚的看到哪里是高密度的区域了。除了区域密度，我们更关心房价的分布。

plt.figure(figsize=(12,12))
 
scatter=plt.scatter(x = df['Longitude'], y = df['Latitude'], label = "Population",
                      c=df['target'], s = df['Population']/100,
                    cmap=plt.get_cmap('jet'))
plt.legend()
plt.colorbar(scatter).set_label("Median_house_value")
plt.show()
复制代码

运行结果如下：

三. Kettle

3.1 什么是Kettle？

Kettle是一款开源的ETL工具,纯java编写,可以在Window、Linux、 Unix上运行,绿色无需安装,数据抽取高效稳定ETL: Extract-Transform-Load的缩写,即数据抽取、转换、装载的过程对各种数据进行处理、转换、迁移,需要掌握一种ETL工具的使用,我们要学习的ETLT具是Kettle

Kettle中文名称叫水壶,该项目的主程序员MATT希望把各种数据放到一个壶里,然后以一种指定的格式流出2006年,Pentaho公司收购了Kettle项目,原Kettle项目发起人Matt Casters加入了Pentaho团队Kettle现在已经更名为PDI:Pentaho Data Integration,即Pentaho数据集成。

3.2 Data Integration

3.3 Kettle界面